はじめに
こんにちは、ヒロです。
エンジニアであれば、よく耳にする「オブジェクト指向」という言葉ですが、抽象的で分かりづらい概念ではないでしょうか?私はオブジェクト指向を理解するのに時間がかかりましたし、これまで十分に活用することができていませんでした。
今回、逆ポーランド記法計算機の実装を要件定義、設計から行っていく中でオブジェクト指向で実装するということがどういうことなのか見えてたので、その経験を記事にしました。オブジェクト指向が分からないという人はぜひ参考にしてみてください。
逆ポーランド記法
逆ポーランド記法というものを知っているでしょうか?私が逆ポーランド記法を初めて知ったのは基本情報技術者試験の時で、その時は何に使うんだろう?と疑問に思っていました。しかし、逆ポーランド記法はスタックマシンモデルと相性が良いため、今回の設計を通してメモリ管理などでも使われるスタックがどういったものなのかを理解する助けにもなりました。
逆ポーランド記法を簡単に説明すると被演算子(数値など)の後に演算子を記述する記法で、以下のような形式で式を記述していく表現方法になります。逆ポーランド記法を使うことで、括弧を書くことなく計算順を指定することができます。後置記法という言い方もされていて、普段使用している式の書き方はこれと対比して中置記法と呼ばれています。
3 4 5 * +
中置記法:3 + 4 * 5
3 4 + 5 *
中置記法:(3 + 4) * 5
スタックマシン
スタックマシンはデータを容器に積み上げていき、取り出す時は最後に入れたものから取り出す、いわゆるLIFO型の配列構造です。最後に入れたものを先に取り出すルールですが、これは容器内のデータを参照する時には影響しません。分かりやすく言い換えると、下が閉じた透明な筒に番号が書いた箱が積み上がっているイメージです。箱は最後に入れたものから取り出していかなければなりませんが、箱の数字は筒が透明なので自由に参照できます。
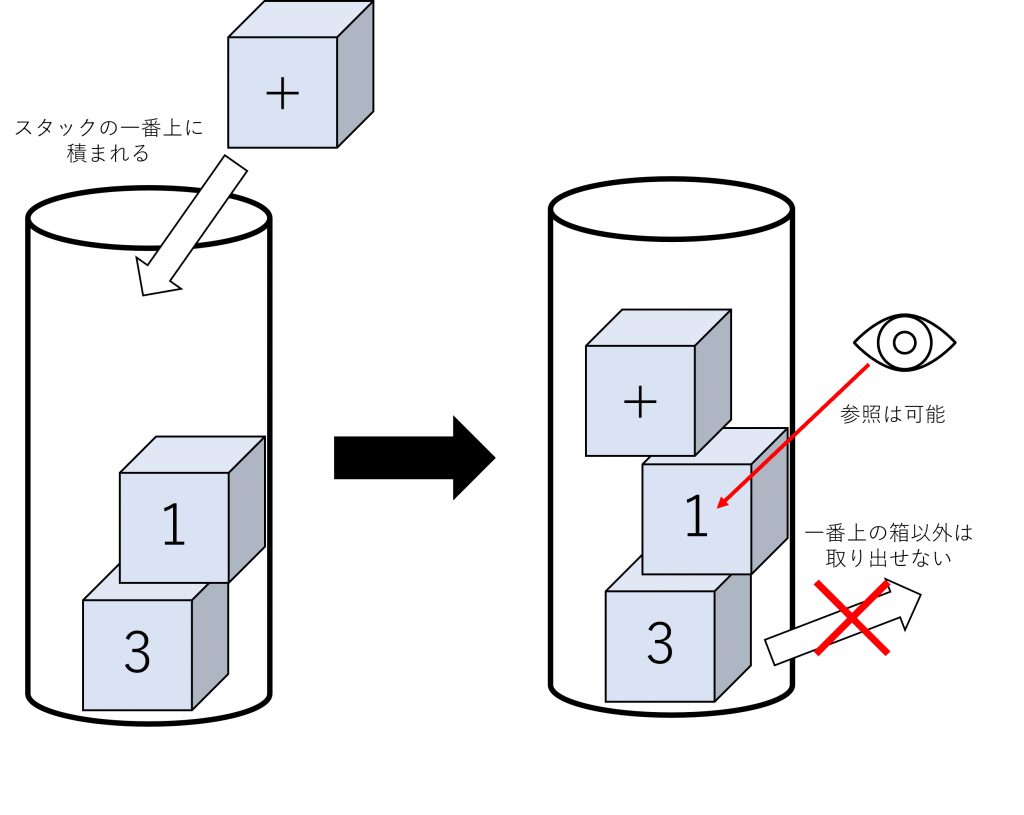
今回はこのスタックマシンに逆ポーランド記法の式を格納していき、最終的に計算ができるようにしていきます。
設計
では、実際に設計に移っていきます。
まず、今回作りたいのは計算機なので式を入力して、その式を実行できなければいけません。誤った式をスタックに格納してしまった時は、その式をスタックから削除する機能も必要です。また、現在どんな式がスタックに格納されているかも分かるようにしたいです。
上で挙げた機能は実際にユーザーが使用する機能なので、外部から参照できるインターフェースとしてこれらの機能を作成します。これが逆ポーランド記法計算機のクラスライブラリで唯一外部から参照できるインターフェースとなります。

先ほどのインターフェースのメソッドがデータを格納したりするスタックを次に作成します。スタックには値の出し入れができる必要があるので、PushメソッドとPopメソッドを用意しています。また、ICalculatorのDisplayメソッドでスタックの中身が見られるようにToArrayメソッドも用意しておきます。
ICalculatorを実装するCalculatorクラスはこのスタックを内部に持ち、スタックを操作していくことで逆ポーランド記法計算を行っていくことになります。
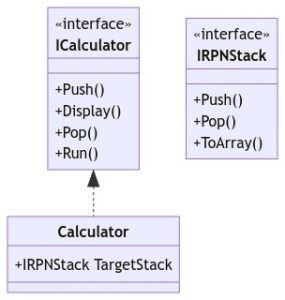
式の挿入機能
次に、ICalculatorのPush処理に焦点を当てて見ていきましょう。
Calculatorに渡される式は文字列として渡されてくることになるので、まずはこれを逆ポーランド記法における式の単位に分割していく必要があります。逆ポーランド記法における式の区切りをどうするかは実装者に委ねられる部分ですが、今回は無難にスペースを利用しています。Calculatorに渡された文字列を個々の式単位に分割する機能をLexicalAnalyzerクラスに持たせました。このクラスは渡された値を分割するだけで、内部に状態を持つ必要がないので、静的なクラスとして実装できます。
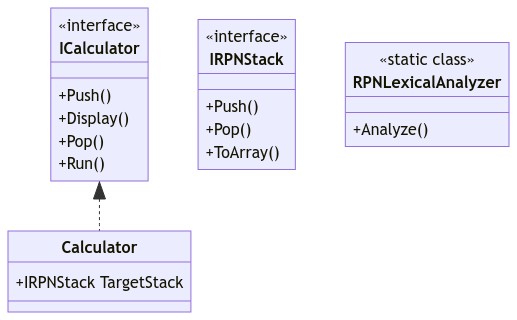
LexicalAnalyzerクラスで分割した個々の式はスタックに格納されることになりますが、どういった形で格納するかで二通りの方法が考えられます。一つ目は記号や数字を分割した文字列そのままに格納する方法で、もう一つは記号や数字を表すクラスを作って、そのクラスを格納する方法です。
一つ目の方法は式をPushする時の処理はたいして考える必要がありません。
しかし、式を実行する時にはその文字列がどんなものかを判断する必要があり、その判断はほぼ間違いなくステートマシン (Switch-Case文)で実装されることになると思います。
これは実装は簡単かもしれませんが、式の種類を追加したい場合などにSwitch-Case文に追加していく必要があり拡張性にすぐれているとは言えません。オブジェクト指向的な設計とも言えないでしょう。
二つ目の方法も一つ目の方法と同じようなステートマシンに落ち着きそうに思えますが、例えばC#で文字列から数値型へ変換する時に使うTryParseメソッドのように、各式や数値のクラスに判別用のメソッドを用意しておくことでステートマシンを書くことなく個々の式を判別することができます。
各クラスのインスタンスはスタックに格納されているので、スタックを上から参照してそれぞれのTryParseメソッドを呼び出すことで自身と一致するクラスをインスタンス化してスタックに新たに格納できます。
今回は二つ目の方法を採用しますが、この方法を使うためにはあらかじめ全ての逆ポーランド記法で記述できる式をスタックに格納しておく必要があります。
さらに、式の定義用のクラスはDisplayメソッドで外部から見えてはいけませんし、Popで取り出すこともRunで実行することもできてはいけません。
ユーザーが入力した式のインスタンスと定義用にあらかじめスタックに格納しておいたインスタンスを区別するため、スタックに格納できるクラスにはIsDefinitionInstanceフラグを持たせます。
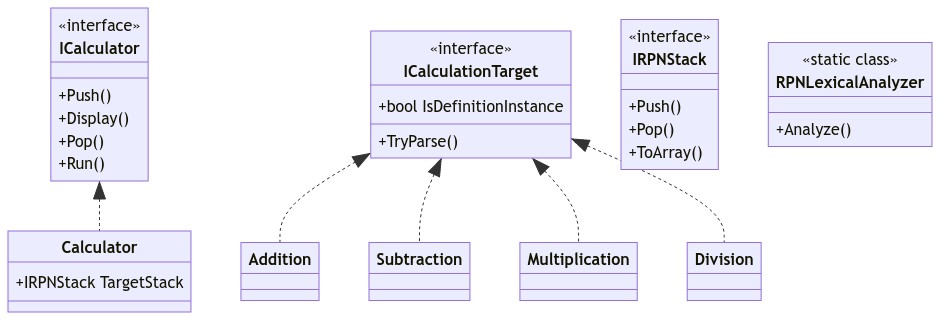
式の取り出し・表示機能
これで、ICalculatorのPushメソッドが呼ばれた時の大まかな構成が決まりました。
次にPopとDisplayですが、Popは基本的にスタックの一番上から一つ値を取り出せば終わりです。
DisplayはPushと同じ要領です。自身を表す文字列を生成して返すメソッドを用意しておいて、スタックを上から参照してそのメソッドを呼ぶだけです。
ただし、PopもDisplayも定義用のインスタンスだった場合は処理をしてはいけません。
足し算ができなかったり、入力していない式が表示されたりするのでは、壊れているのと変わりないでしょう。
式の実行機能
最後にRun機能です。
逆ポーランド記法の計算ではスタックの上から値を取り出し、その値が四則演算記号であればさらに二つの値をスタックから取り出します。取り出した二つの値に対して同じことを繰り返していきます。つまり、取り出した値が数値ならそのまま計算に使い、四則演算記号であればさらにスタックから二つの値を取り出します。いわゆる再帰呼び出しの構図になります。
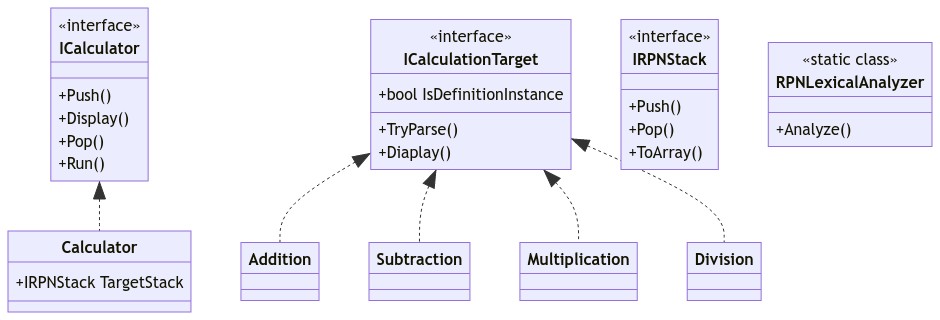
ここまでの設計でスタックに格納するクラスの構成が決まってきました。これをICalculationTargetとしてインターフェースにしておきます。四則演算の処理は実際に計算するところ以外のスタックの操作部分は全く同じ処理になるので、ICalculationTargetを実装した抽象クラスを作成し、そこに共通処理は実装してしまいます。そして、四則演算の記号クラスはICalculationTargetではなく、抽象化クラスを継承するように変更します。
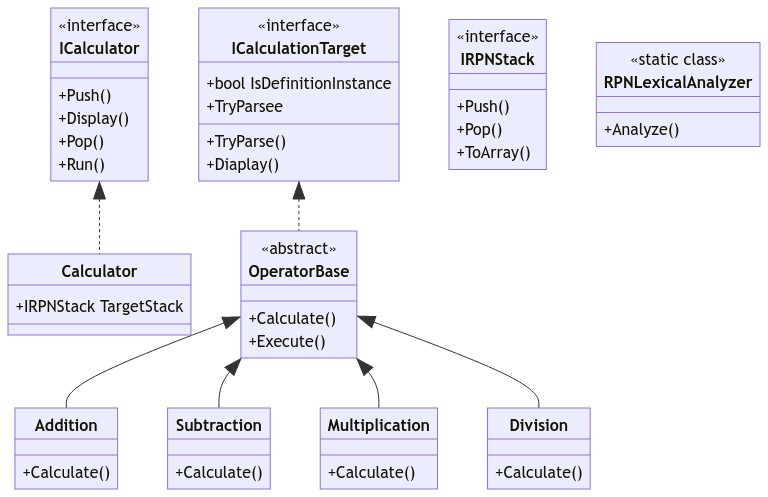
これで、四則演算が実行できる逆ポーランド記法計算のライブラリの設計が完了しました。
あとがき
ここまで、この記事を読んでいただきありがとうございます。
オブジェクト指向などの抽象的な概念を理解する時にいきなり実装から入ってしまうとよく分からなくなってしまうことが多々あると思います。そういった時は急がば回れではないですが、一歩引いて簡単な図で表してみたりすると分かるようになるかもしれません。実装なしでも学べることは多いと思うので、オブジェクト指向がよく分からないという人はスタックマシンを使った逆ポーランド記法計算機の設計をぜひ試してみてください。

