はじめに
量子コンピュータの研究が盛んである。Google、IBM、Intelなどの巨大テック企業が多額の資金を投入し研究を行なっている。昨年には、Googleが世界で初めて量子優越性(Quantum Supremacy)を示したと主張し話題となった(例えばこれ)。今回は、量子コンピュータが計算を行う際の基本単位となる「量子ビット」について簡単な解説を行う。
古典ビット
我々が日常使うコンピュータは数値を2進数で表す。すなわち、コンピュータが計算する際の基本単位は、0か1のどちらか一方の状態をとる「ビット」と呼ばれる量である。量子コンピュータと従来型のコンピュータの比較を行うとき、現在のコンピュータを古典コンピュータと呼び、その基本単位であるビットを古典ビットと呼ぶことが多い。
古典ビットは0か1のどちらか一方の状態をとる。
量子ビット
量子コンピュータが計算する際の基本単位は量子ビット(quantum bit:qビット)と呼ばれ、0状態と1状態の「重ね合わせ」で表される。これを数式で表現すると
(1) ![]()
となる。ここで、![]() は列ベクトルを表し、量子力学ではケットベクトルと呼ばれる量である。
は列ベクトルを表し、量子力学ではケットベクトルと呼ばれる量である。![]() と
と![]() は
は
(2) 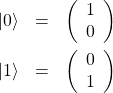
で定義される。また![]() と
と![]() は確率振幅と呼ばれる量であり複素数である。量子力学では、確率振幅の絶対値の2乗が確率を表すので、式(1)は次のように解釈される。すなわち、状態
は確率振幅と呼ばれる量であり複素数である。量子力学では、確率振幅の絶対値の2乗が確率を表すので、式(1)は次のように解釈される。すなわち、状態![]() が
が![]() である確率が
である確率が![]() 、
、![]() である確率が
である確率が![]() である。確率であるから次式が成り立つ。
である。確率であるから次式が成り立つ。
(3) ![]()
これは、状態![]() の規格化条件である。
の規格化条件である。![]() のとき
のとき![]() 、
、![]() のとき
のとき![]() となるから、量子ビットは古典ビットを包含する概念である。
となるから、量子ビットは古典ビットを包含する概念である。
量子ビットは0と1の重ね合わせの状態で表される。
量子ビットの可視化
式(1)(量子ビット)を視覚的に理解するため、これを3次元空間内に描画してみる。まず最初に、![]() と
と![]() を極座標で表す。
を極座標で表す。
(4) ![]()
ここで、![]() は正の実数、
は正の実数、![]() は実数である。規格化条件(3)は
は実数である。規格化条件(3)は
(5) ![]()
(6) 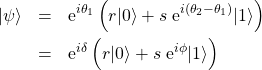
となる。ただし、![]() とした。
とした。![]() である。量子力学において物理的に意味があるのは確率振幅の2乗である。従って、式(6)のように式全体にかかる位相(
である。量子力学において物理的に意味があるのは確率振幅の2乗である。従って、式(6)のように式全体にかかる位相(![]() )は確率には寄与しないため、これを1に置き換えることができる。
)は確率には寄与しないため、これを1に置き換えることができる。
(7) ![]()
![]() は規格化条件(5)を満たすので
は規格化条件(5)を満たすので
(8) ![]()
と書くことができる。どちらも正の数なので、![]() として良い。後の便宜のため
として良い。後の便宜のため![]() を
を![]() に置き換える。
に置き換える。
(9) 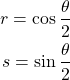
このとき範囲は![]() となる。上式を式(7)に代入すると
となる。上式を式(7)に代入すると
(10) ![]()
を得る。式(2)を代入して計算すると
(11) ![]()
となる。最終的に量子ビットの状態![]() は、
は、![]() が
が![]() の範囲を動くときの式(11)で表すことができる。ところで、3次元空間内の点を極座標で表すと
の範囲を動くときの式(11)で表すことができる。ところで、3次元空間内の点を極座標で表すと
(12) 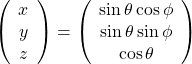
と書くことできる。![]() が
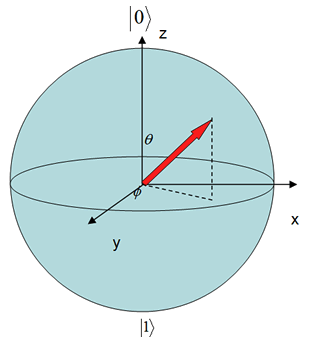
が![]() の範囲を動くとき、この点は半径1の球面上を動く。すなわち、式(11)と球面上の点は一対一に対応することになる(下図参照)。
の範囲を動くとき、この点は半径1の球面上を動く。すなわち、式(11)と球面上の点は一対一に対応することになる(下図参照)。
![]() のとき
のとき![]() 、
、![]() のとき
のとき![]() となる。この球は量子力学ではBloch(ブロッホ)球と呼ばれる。これを地球と見なせば古典ビットは、北極と南極の2点に相当する。一方、量子ビットの状態は、球面上の任意の点に相当する。
となる。この球は量子力学ではBloch(ブロッホ)球と呼ばれる。これを地球と見なせば古典ビットは、北極と南極の2点に相当する。一方、量子ビットの状態は、球面上の任意の点に相当する。
古典ビットは北極と南極だけを表すに過ぎないが、量子ビットは球面上の任意の点を表すことができる。
まとめ
今回は、量子ビットの簡単な説明を行なった。量子コンピュータの並列性の高さや高速さの源は、状態の重ね合わせを利用するところにある。その基本単位である量子ビットを視覚的に理解するため、Bloch球の導出を行なった。
古典ビットの状態は2値化されているが、量子ビットの状態は連続値である。したがって、前者はデジタル、後者はアナログと見ることもできる。アナログであるがゆえにノイズに大変敏感である。これに対処するため、現在作られている量子コンピュータは装置自体がかなり大掛かりになるようである。