はじめに
最近注目されている量子アニーリングについて概説する。
イジング模型
最初に、イジング模型と呼ばれる模型について説明する。下図に示すような格子を定義し、格子点上に「スピン」が配置されている系を考える。
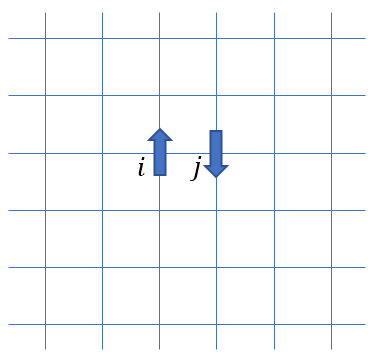
本稿ではスピンという言葉を、+1と-1のいずれか一方の値を持つ変数として用いる(量子力学的に厳密な定義には触れない)。これをスピン変数と呼ぼう。上図では+1を上向きスピン、-1を下向きスピンとして表した。図では2つの格子点![]() 上にしかスピンを描いていないが、全格子点上にスピンは配置されている。次に、任意の格子点のペア
上にしかスピンを描いていないが、全格子点上にスピンは配置されている。次に、任意の格子点のペア![]() の間に重み(相互作用)
の間に重み(相互作用)![]() を導入し、次式を考える。
を導入し、次式を考える。
(1) ![]()
ここで、![]() はスピン変数である。また、
はスピン変数である。また、![]() は格子点上の全スピン変数を表す。
は格子点上の全スピン変数を表す。![]() は、重複を除いた全ペアについて和をとることを意味する。式(1)をイジング模型と呼ぶ。
は、重複を除いた全ペアについて和をとることを意味する。式(1)をイジング模型と呼ぶ。
量子アニーリングなる手法(後述)で実現したい目的は、式(1)を最小にする![]() の組み合わせを見つけることである。この難しさを具体的に見るため、三角形の3つの頂点上にスピンが定義されたイジング模型を考える(下図参照)。ペア間の相互作用を定数
の組み合わせを見つけることである。この難しさを具体的に見るため、三角形の3つの頂点上にスピンが定義されたイジング模型を考える(下図参照)。ペア間の相互作用を定数![]() とする。このときイジング模型は次式となる。
とする。このときイジング模型は次式となる。
(2) ![]()
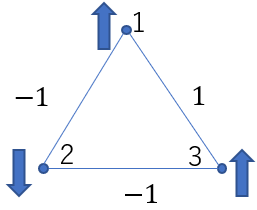
上図は![]() のときである。このとき
のときである。このとき
(3) 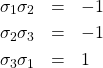
が成り立つので、![]() である。上図の辺上に各スピン対の相互作用の大きさを示した。もう一度注意深く上の図を眺めると、
である。上図の辺上に各スピン対の相互作用の大きさを示した。もう一度注意深く上の図を眺めると、![]() のペアのスピンはお互いに逆向きであり、
のペアのスピンはお互いに逆向きであり、![]() は最小値-1になっている。同様に、
は最小値-1になっている。同様に、![]() のペアも逆向きであり
のペアも逆向きであり![]() は最小値-1になっている。最後のペア
は最小値-1になっている。最後のペア![]() も逆向きにとれれば、総和である
も逆向きにとれれば、総和である![]() を最小にできるはずである。しかしながら、このペアを逆向きにとると、今度は
を最小にできるはずである。しかしながら、このペアを逆向きにとると、今度は![]() のペアが同じ向きを向いてしまう。このような「あちらを立てればこちらが立たず」の状態をフラストレーションと呼ぶ。局所的な状態の最小値が系全体の最小値にならないことを示す言葉である。
のペアが同じ向きを向いてしまう。このような「あちらを立てればこちらが立たず」の状態をフラストレーションと呼ぶ。局所的な状態の最小値が系全体の最小値にならないことを示す言葉である。
一般のイジング模型では、ペア間の相互作用![]() は任意の実数値を取り得るため、式(1)を最小化するスピン変数の組を探す問題は大変難しい。式(1)を最小にするスピンの組を探すことを物理の言葉で「基底状態」を探すと言う。また、式(1)を「ハミルトニアン」、
は任意の実数値を取り得るため、式(1)を最小化するスピン変数の組を探す問題は大変難しい。式(1)を最小にするスピンの組を探すことを物理の言葉で「基底状態」を探すと言う。また、式(1)を「ハミルトニアン」、![]() の最小値を「基底エネルギー」と呼ぶ。
の最小値を「基底エネルギー」と呼ぶ。
量子アニーリング
イジング模型の基底状態を量子効果を用いて求める方法が量子アニーリングである。本稿では量子効果の詳細は割愛し、量子アニーリングの概略だけを説明する。最初に、次のイジング模型を考える。
(4) ![]()
ここで、![]() はこれまでのような(-1,+1)のいずれかの値を取るスピン変数ではなく、パウリ行列の
はこれまでのような(-1,+1)のいずれかの値を取るスピン変数ではなく、パウリ行列の![]() 軸成分と呼ばれるものである(
軸成分と呼ばれるものである(![]() の行列)。スピン変数をパウリ行列に置き換えることにより量子効果を取り入れることができる(そういうものであると認めてほしい)。量子アニーリングの目的は、
の行列)。スピン変数をパウリ行列に置き換えることにより量子効果を取り入れることができる(そういうものであると認めてほしい)。量子アニーリングの目的は、![]() の基底状態
の基底状態![]() を見つけることである。
を見つけることである。
ところで、![]() 軸とは垂直な方向の
軸とは垂直な方向の![]() 軸成分
軸成分![]() を考え、次のハミルトニアンも考える。
を考え、次のハミルトニアンも考える。
(5) ![]()
この項は、スピンの向き(![]() 軸方向)に対し垂直な方向に磁場をかけることにより生じるエネルギーなので、「横磁場項」と呼ばれる。この基底状態は簡単に求めることができる。いまこれを
軸方向)に対し垂直な方向に磁場をかけることにより生じるエネルギーなので、「横磁場項」と呼ばれる。この基底状態は簡単に求めることができる。いまこれを![]() と書くことにする。量子アニーリングでは、答えの分かっている自明な基底状態
と書くことにする。量子アニーリングでは、答えの分かっている自明な基底状態![]() を、時間をかけてゆっくりと非自明な基底状態
を、時間をかけてゆっくりと非自明な基底状態![]() に変化させていく。これを実現するため、時間に依存する2つの係数
に変化させていく。これを実現するため、時間に依存する2つの係数![]() を導入し、次のハミルトニアンを考える。
を導入し、次のハミルトニアンを考える。
(6) ![]()
![]() の時間変化は下図の通りである。
の時間変化は下図の通りである。
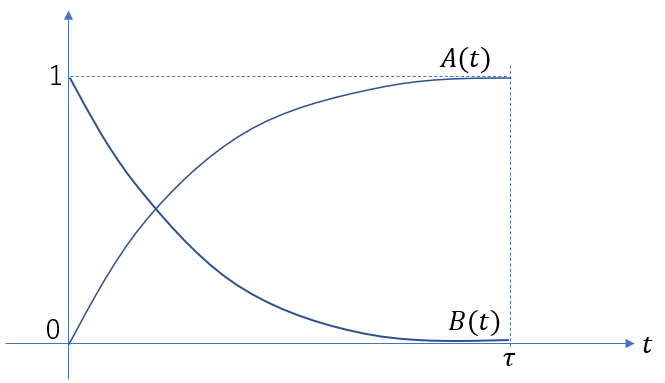
非常に長い時間![]() をかけて
をかけて![]() をゆっくりと変化させる。時刻
をゆっくりと変化させる。時刻![]() のハミルトニアンは
のハミルトニアンは![]() であり自明な基底状態
であり自明な基底状態![]() を持つ。その状態からゆっくりと
を持つ。その状態からゆっくりと![]() を変化せていくと、基底状態が
を変化せていくと、基底状態が![]() に変化していく(下図参照)。
に変化していく(下図参照)。
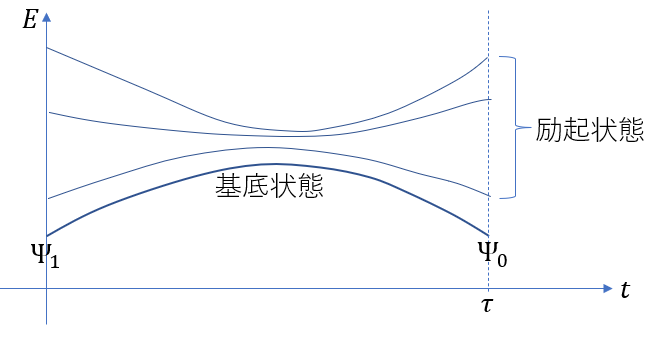
この一連の手順を量子アニーリングと呼ぶ。ゆっくりと変化させないと励起状態(基底状態より高いエネルギーを持つ状態)に遷移してしまうので注意が必要である。ここで注目すべきことは、基底状態の変化は、自然の摂理に従って(すなわち量子力学の原理に従って)起こるということである。人間が調節するのは![]() だけである。
だけである。![]() さえ調節してやればあとは勝手に基底状態が決まるのである。
さえ調節してやればあとは勝手に基底状態が決まるのである。
最後に、量子アニーリングの対象となる実際のチップを示す(ここから引用した)。このチップ上に、本稿の一番最初に示した格子が実装され、その格子点上に量子力学的なスピンが配置されている。

最適化問題をイジング模型に落とし込むことができれば、量子アニーリングを用いて、基底状態(最適なパラメータの組)を求めることできる。その一例として巡回セールスマン問題(Traveling Salesman Problem:TSP)を考える。
巡回セールスマン問題(TSP)
決められた都市をすべて1度ずつ訪れて元の都市に戻ってくるための最短経路を探すのが巡回セールスマン問題である(下図参照)。
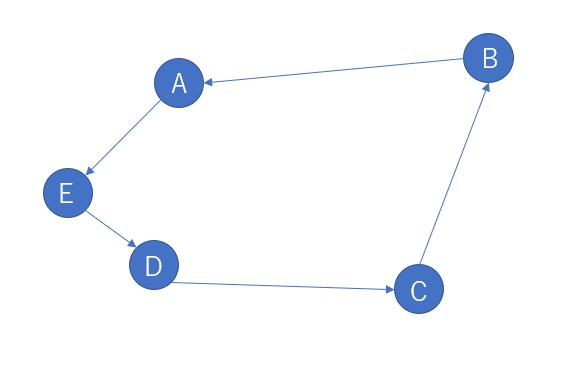
上図は5都市の巡回セールスマン問題である。AからEまでの点を結ぶ最短経路を探すことになる。5都市の巡回セールスマン問題をイジング模型で表すため、5×5の表を作る。
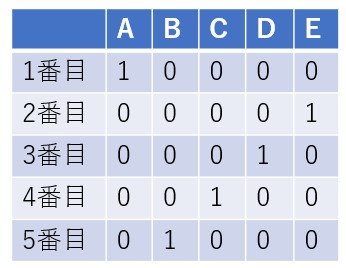
この表は、1番目にA都市を訪れ、2番目にE都市を訪れ、3番目にD都市を訪れることを表している。経路を1つ決めるとそれに対応する表を1つ作ることができる。いま、都市![]() かつ
かつ![]() 番目のマスに入れる変数を
番目のマスに入れる変数を![]() と書くことにする。また、都市
と書くことにする。また、都市![]() と
と![]() の間の距離を
の間の距離を![]() とすると、全経路の長さ
とすると、全経路の長さ![]() は
は
(7) 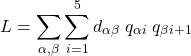
となる。![]() は0か1であるから、
は0か1であるから、![]() と
と![]() がともに1のときのみ、距離が加算される。さて、上の表をもう一度眺めると、各行の数字の和は常に1であることが分かる。これは、1度に訪れることできる場所は1か所だけであることを表している。さらに、各列の数字の和も常に1である。これは、各都市には1度だけ訪れることを表している。この2つの束縛条件を式(7)に追加する。
がともに1のときのみ、距離が加算される。さて、上の表をもう一度眺めると、各行の数字の和は常に1であることが分かる。これは、1度に訪れることできる場所は1か所だけであることを表している。さらに、各列の数字の和も常に1である。これは、各都市には1度だけ訪れることを表している。この2つの束縛条件を式(7)に追加する。
(8) 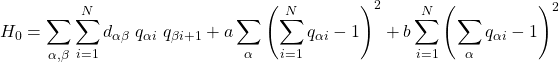
上式において、都市の数5を一般の数![]() に置き換えた。0と1の値を取る変数
に置き換えた。0と1の値を取る変数![]() を-1,+1の値を持つスピン変数に置き換えれば、イジング模型のハミルトニアンになる。さらに、パウリ行列に置き換えれば、量子アニーリングを用いて解くことができるハミルトニアンになる。
を-1,+1の値を持つスピン変数に置き換えれば、イジング模型のハミルトニアンになる。さらに、パウリ行列に置き換えれば、量子アニーリングを用いて解くことができるハミルトニアンになる。![]() はそれぞれの束縛条件をどの程度重視するかを決める係数である。式(8)が式(6)の
はそれぞれの束縛条件をどの程度重視するかを決める係数である。式(8)が式(6)の![]() に相当する。ここに横磁場項
に相当する。ここに横磁場項![]() を加えて量子アニーリングを行い、最適解(
を加えて量子アニーリングを行い、最適解(![]() の基底状態)を見つけることになる。
の基底状態)を見つけることになる。
量子アニーリングの現状
TSPを含む最適化問題に適用される解法には以下の3つがある。
今回説明した量子アニーリングが属するのは、3番目の発見的解法である。TSPは歴史の長い問題であり、現在では、85,900都市の厳密解と1,904,711都市の近似解が求められている。いずれも量子アニーリングを用いない手法である。また、普通のPCでも2392都市の厳密解を1分もかからずに解くことができる(動画)。さらに、このページでは、3次元のTSPの現状が紹介されている。これを見ると、1,331,906,450地点の3次元TSPの近似解が存在することが分かる。
一方、現在の量子アニーリングで解けている最大の都市数はいくつなのかを調べたが、明確な数を記載したページが見つからなかった。ところで、量子アニーリングを従来のGPUやFPGAを用いて模倣したマシンを東芝が出している。これは現在の量子アニーリングよりも多くのスピンを扱うことができるので、TSPの都市数も量子アニーリングより大きくすることができるが、それでも数十都市が限界のようである(参照サイト)。
量子アニーリングの優位性を謳うのにTSPを例に取り上げる記事を多く見かけるが、上で見るように正しい主張ではない。ビジネストークであると割り切る必要がある。最近、量子アニーリングを搭載したマシンを開発している唯一の企業であるD-wave社が、量子ゲート方式の開発も始めると言うアナウンスがあった(例えばこの記事)。量子アニーリングだけではビジネスが成り立たないと言うことであろう(おそらく)。

