はじめに
今回は点群処理の前処理としてしばしば使われるFarthest Point Sampling(FPS)を紹介する。本手法は密な点群が手元にあるとき、あらかじめ決めた点(3次元座標)の数に「良い具合に」間引くものである。
アルゴリズム
アルゴリズムは以下の通りである。
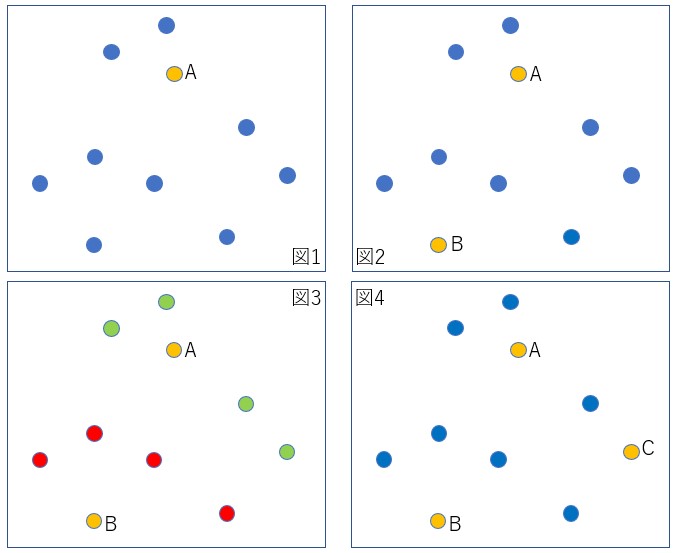
- 最初に、与えられた点群から適当に1点を選びこれをAとする(図1)。
- 次にAから最も離れた点を見つけこれをBとする(図2)。
- 残りの点とA,Bとの距離を計算し、より短い方の距離を記録する。図3では、Aに近い点を緑で、Bに近い点を赤で塗分けた。
- これらの距離の中で最も長い距離を持つ点をCとする(図4)。図4の場合は、最も長い距離は緑点に属している。
- 選択した点が所定の数になるまで繰り返す。
とても単純な処理であるが、空間的な位置関係を見ながら間引くので、乱数で点を選ぶ場合より「良い塩梅」の結果を得ることができる。
実行結果
上のアルゴリズムをC++で実装した。ソースはここにある。以下の結果は、113662個の点群(図5の青点)から1000個の点群(図6の黒点)に間引いた結果である。比較のため乱数で1000個の点を選んだ結果も示す(図7の黒点)。図6と7の点のサイズは見やすさのため大きくしてある。
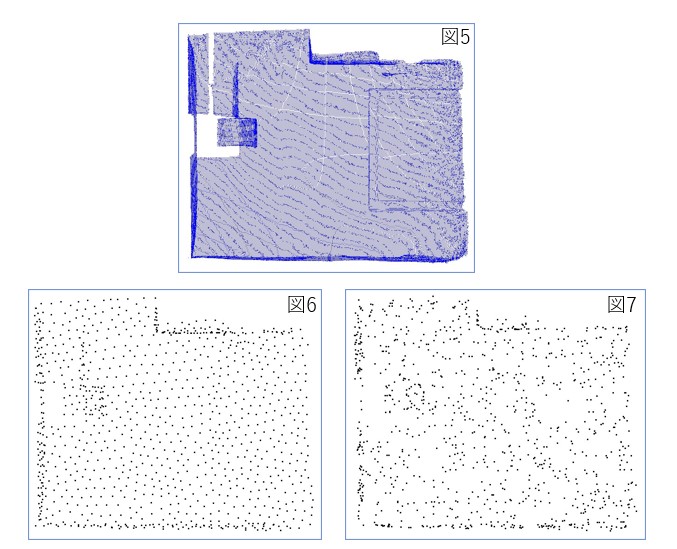
本手法(図6)の方が空間的に一様に点を選択できていることが分かる。
コード
以下はFPSを実行する関数である。cloudは入力点群を格納した配列、kは選択したい点の数である。このコードの肝はmin_distancesである。この配列の中に各点と選択点との最短距離が記録される(29行目)。そして、その中から最大の距離を持つ点が選ばれる(20行目)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
auto execute_farthest_point_sampling(const std::vector<cv::Vec3f>& cloud, int k) -> std::vector<cv::Vec3f> { // 選択された点のインデックスを格納する配列(k個の0で初期化) auto indices = std::vector<int>(k, 0); // 入力点群の点数 const auto cloud_size = std::size(cloud); // 乱数を生成し、最初の点を決める。 const auto index = generate_random_value(1, cloud_size); cv::Vec3f farthest_point = cloud[index]; // 点の登録 indices[0] = index; // 他の点との距離を計算 auto min_distances = calcualte_distances(farthest_point, cloud); // (1,cloud_size) for (auto i = 1; i < k; ++i) { // 最も距離の長い点のインデックスを見つけ、indicesに登録する。 indices[i] = argmax(min_distances.begin<float>(), min_distances.end<float>()); // 新たな最遠点 farthest_point = cloud[indices[i]]; // 他の点との距離を計算 const auto tmp = calcualte_distances(farthest_point, cloud); // min_distancesの更新 min_distances = minimum(min_distances, tmp); } std::vector<cv::Vec3f> new_cloud{}; new_cloud.reserve(k); for (auto& index : indices) { new_cloud.emplace_back(cloud[index]); } return new_cloud; } |
まとめ
今回は、点群の前処理として使われるFPSを紹介した。FPSは点の数をあらかじめ決めた数になるように間引く処理である。点群処理においても最近では深層学習が使われることが多い。深層学習では、入力データ(画像やベクトル)は固定サイズであることがほとんどであるからFPSが使われる機会は多い。

