はじめに
最近、「ビジュアル リーマン予想入門」という本を読んでいる。リーマン予想を一般人向けに詳しく解説した本である。この本の中に「非自明零点から素数を作る」と題した解説があるが、大変面白かったので紹介する(数学に詳しい人には当たり前のことかもしれないけれど)。
リーマン予想
リーマン予想とは以下の予想のことである(引用元)。
ゼータ函数の非自明な零点はすべてクリティカルライン上にある。
上の文言に出てくる以下の専門用語を簡単に解説する。
- ゼータ函数
- 零点
- 非自明な零点
- クリティカルライン
ゼータ函数とは次式で定義される函数である。
(1) ![]()
ここで、![]() は複素数である。厳密に言うと「解析接続」という手順を踏んで定義域を拡大したものがゼータ函数となる。ここではこの手順を既に終えているものとする。次式を満たす
は複素数である。厳密に言うと「解析接続」という手順を踏んで定義域を拡大したものがゼータ函数となる。ここではこの手順を既に終えているものとする。次式を満たす![]() をゼータ函数の零点と呼ぶ。
をゼータ函数の零点と呼ぶ。
(2) ![]()
零点には以下の2種類がある。
- 自明な零点:負の偶数。

- 非自明な零点:自明な零点以外の零点
非自明な零点は、![]() の実部が
の実部が![]() の直線上にあると言われている(これがリーマン予想である)。この直線のことをクリティカルラインと呼ぶ(下図参照)。複素平面の上半分と下半分にある非自明な零点は複素共役な関係にある。
の直線上にあると言われている(これがリーマン予想である)。この直線のことをクリティカルラインと呼ぶ(下図参照)。複素平面の上半分と下半分にある非自明な零点は複素共役な関係にある。
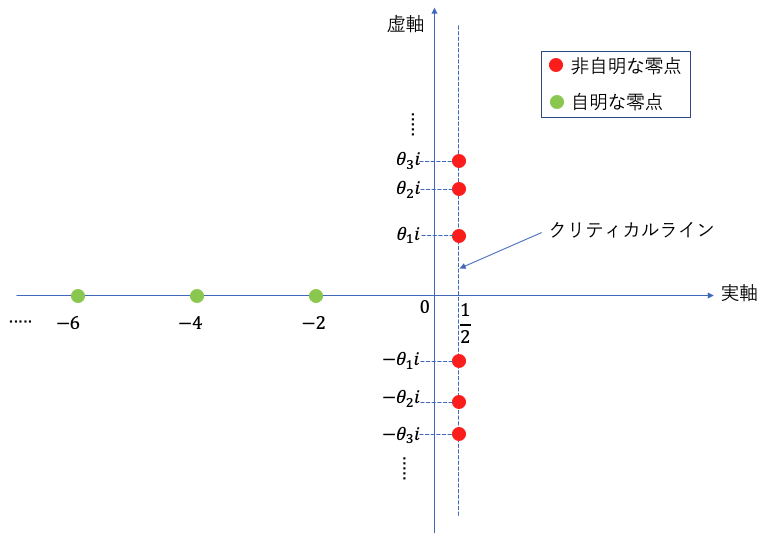
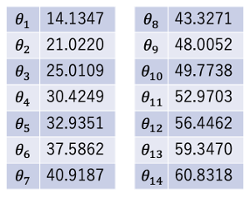
非自明な零点の最初の14個を以下に示す。
素数を作る
ここからが本題。上の表に掲げた非自明な零点と次式を使うと素数を作ることができる。
(3) 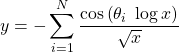
![]() としたときのグラフを以下に示す。実装したコードはここにある。Python版とJulia版を作成した。
としたときのグラフを以下に示す。実装したコードはここにある。Python版とJulia版を作成した。
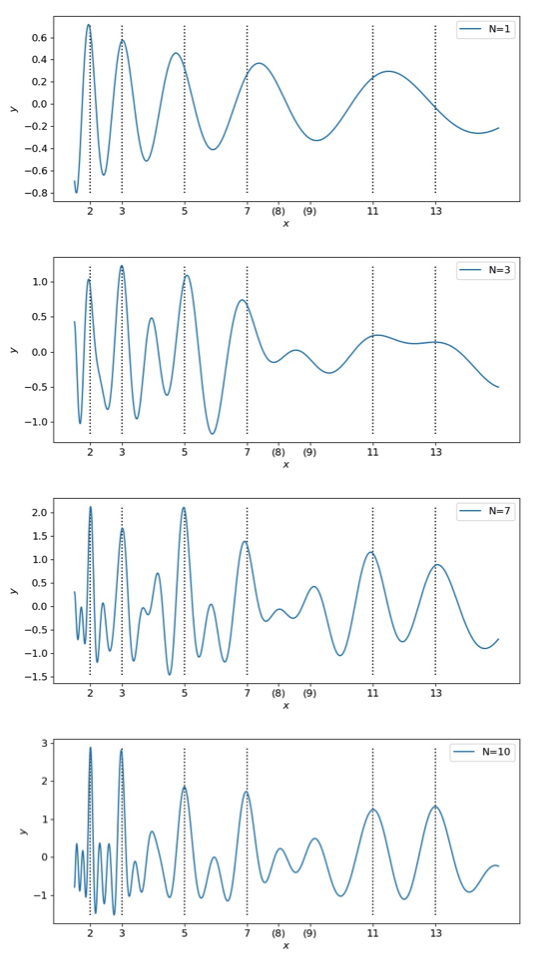
垂直な点線は、素数の位置を表す。![]() を大きくしていくと、極大値の位置が徐々に素数と一致していく様子が分かる。素数の位置だけでなく素数の累乗の位置にも極大値が現れ始める(
を大きくしていくと、極大値の位置が徐々に素数と一致していく様子が分かる。素数の位置だけでなく素数の累乗の位置にも極大値が現れ始める(![]() )。
)。![]() としたときの様子が、ビジュアル リーマン予想入門のp181に掲載されている。それを見ると、素数とその累乗の位置に背の高い鋭いピークが存在することを確認できる。
としたときの様子が、ビジュアル リーマン予想入門のp181に掲載されている。それを見ると、素数とその累乗の位置に背の高い鋭いピークが存在することを確認できる。
まとめ
今回は、ゼータ函数の非自明な零点から素数を作ることができることを紹介した。ゼータ函数と素数の間には次式が成り立つことも知られている。
(4) ![]()
ここで、![]() は素数である。素数とゼータ函数の間には密接な関係があり、とても興味深い。
は素数である。素数とゼータ函数の間には密接な関係があり、とても興味深い。

