はじめに
いま話題の3D Gaussian Splattingを最初に提案した論文「3D Gaussian Splatting for Real-Time Radiance Field Rendering」の中に、クォータニオン(Quaternion)を構成する4つの成分から回転行列を導出する式が記載されていた。この表式はクォータニオンの入門書には必ず示されているものである。今回はこの式の導出を行う。論文自体の紹介は機会を改める。
クォータニオンとは
クォータニオンとは、主に3Dコンピュータグラフィックス(3DCG)の世界で使われる手法である。クォータニオンを使うと回転を直感的に表現することができ、回転の関わる計算が容易になるため、3DCGの世界では頻繁に使われる。まず最初にクォータニオン![]() を定義しよう。
を定義しよう。
![]()
ここで、![]() は実数であり、
は実数であり、![]() に対しては次式が成り立つ。
に対しては次式が成り立つ。
![]()
クォータニオンは複素数を拡張したような数である。さて、計算時の表記を簡略化するため以下の表記を導入する。
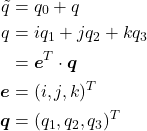
![]() 、
、![]() をそれぞれクォータニオンの実部、虚部と呼ぶ。また、
をそれぞれクォータニオンの実部、虚部と呼ぶ。また、![]() は転置を表し、
は転置を表し、![]() は2つのベクトル間の内積である。次に、2つのクォータニオンの積を計算してみよう。
は2つのベクトル間の内積である。次に、2つのクォータニオンの積を計算してみよう。
![]()
(1) ![]()
が成り立つ。ただし、![]() とおいた。
とおいた。![]() はクォータニオンの虚部同士の積であり、その積が
はクォータニオンの虚部同士の積であり、その積が![]() と
と![]() の内積と外積から構成されることに注意する。また、
の内積と外積から構成されることに注意する。また、![]() は実部と虚部に分けることができるから、クォータニオン同士の積もクォータニオンになることが分かる。次に、
は実部と虚部に分けることができるから、クォータニオン同士の積もクォータニオンになることが分かる。次に、![]() に共役なクォータニオン
に共役なクォータニオン![]() を次式で定義する。
を次式で定義する。
![]()
これを使うと
![]()
を得る。これより![]() の長さを次式で定義できる。
の長さを次式で定義できる。
![]()
回転行列
ここではクォータニオンから離れて回転行列について解説する。話を簡単にするため、![]() 軸周りを
軸周りを![]() だけ反時計回りに回転する行列を取り上げる。
だけ反時計回りに回転する行列を取り上げる。
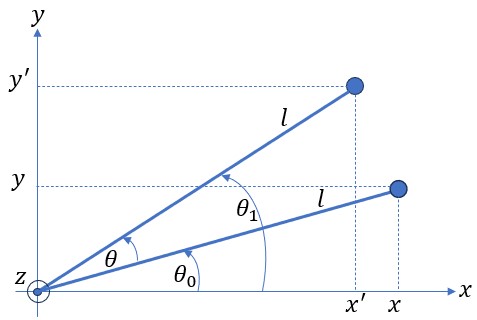
右図において次式が成り立つ。
![]()
![]() を用いて
を用いて![]() を変形すると
を変形すると
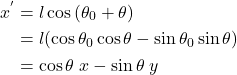
を得る。同様に![]() を変形すると
を変形すると
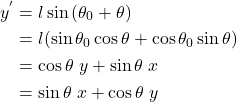
となる。この2式から回転行列を構成することができる。
![]()
これを3次元に拡張すれば次式を得る。
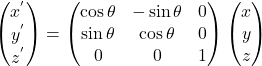
右辺に現れる行列が、![]() 軸周りを反時計回りに
軸周りを反時計回りに![]() だけ回転する行列
だけ回転する行列![]() である。
である。
クォータニオンによる回転行列の表記
上で求めた回転行列![]() を、クォータニオンを用いて書くことができる。最初に次のクォータニオンを用意する。これは単位ベクトル
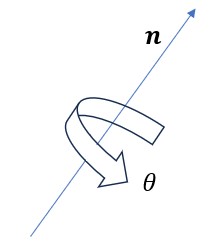
を、クォータニオンを用いて書くことができる。最初に次のクォータニオンを用意する。これは単位ベクトル![]() の周りを反時計回りに
の周りを反時計回りに![]() だけ回転するクォータニオンを表す(右図参照)。
だけ回転するクォータニオンを表す(右図参照)。
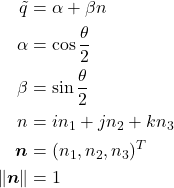
クォータニオンで回転を表現する際は、![]() が要求される。上式がこれを満たしていることは以下のように確認できる。
が要求される。上式がこれを満たしていることは以下のように確認できる。
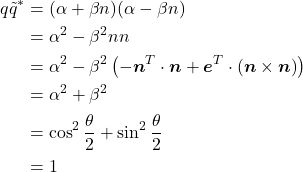
さて
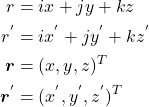
とおくと、![]() を軸
を軸![]() の周りに回転した
の周りに回転した![]() を、
を、![]() で求めることができる。これを計算すると
で求めることができる。これを計算すると
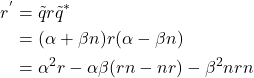
となる。ここで、![]() と
と![]() はクォータニオンの虚部同士の積であり式(1)を用いて計算することができる。
はクォータニオンの虚部同士の積であり式(1)を用いて計算することができる。
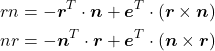
さらに、上の2番目の式を使うと
![Rendered by QuickLaTeX.com \begin{align*} nrn &=\left(-\boldsymbol{n}^T\cdot\boldsymbol{r}+\boldsymbol{e}^T\cdot(\boldsymbol{n}\times\boldsymbol{r})\right)n \\ &=-(\boldsymbol{n}^T\cdot\boldsymbol{r})n+\left[\boldsymbol{e}^T\cdot(\boldsymbol{n}\times\boldsymbol{r})\right]n\\ &=-(\boldsymbol{n}^T\cdot\boldsymbol{r})n-(\boldsymbol{n}\times\boldsymbol{r})^T\cdot\boldsymbol{n}+\boldsymbol{e}^T\cdot \left[(\boldsymbol{n}\times\boldsymbol{r})\times\boldsymbol{n}\right]\;\;\;(\because (1))\\ &=-(\boldsymbol{n}^T\cdot\boldsymbol{r})n-(\boldsymbol{n}\times\boldsymbol{r})^T\cdot\boldsymbol{n}+\boldsymbol{e}^T\cdot \left[-(\boldsymbol{n}^T\cdot\boldsymbol{r})\cdot\boldsymbol{n}+\boldsymbol{r} \right]\\ &=-(\boldsymbol{n}^T\cdot\boldsymbol{r})n+\boldsymbol{e}^T\cdot \left[-(\boldsymbol{n}^T\cdot\boldsymbol{r})\cdot\boldsymbol{n}+\boldsymbol{r} \right]\;\;\;(\because (\boldsymbol{n}\times\boldsymbol{r})^T\cdot\boldsymbol{n}=0)\\ &=\boldsymbol{e}^T\cdot\left\{ -(\boldsymbol{n}^T\cdot\boldsymbol{r})\boldsymbol{n}+ \left[-(\boldsymbol{n}^T\cdot\boldsymbol{r})\cdot\boldsymbol{n}+\boldsymbol{r} \right]\right\}\;\;\;(\because n=\boldsymbol{e}^T\cdot\boldsymbol{n}) \end{align*}](/wp-content/ql-cache/quicklatex.com-fb4c27f12460f5782ba94d9ba48b25c1_l3.png)
を得る。これらを代入すると
![]()
となる。![]() であるから
であるから
![]()
を得る。![]() を代入して少し計算すると
を代入して少し計算すると
![]()
となる。これが、![]() を単位ベクトル
を単位ベクトル![]() の周りに反時計回りに
の周りに反時計回りに![]() だけ回転させる式である。いま、
だけ回転させる式である。いま、![]() とすれば上で求めた回転行列
とすれば上で求めた回転行列![]() が導出される。
が導出される。
クォータニオンによる回転行列の表記(一般化)
論文「3D Gaussian Splatting for Real-Time Radiance Field Rendering」に載っていた式はもっと一般的な回転行列であったので最後にこれを求めてお終いにしたい。回転を表すクォータニオン![]() を
を![]() に作用させる。ここで
に作用させる。ここで![]() が満たされていることに注意する。
が満たされていることに注意する。
![]()
これをゴリゴリと計算すると
![]()
となり
![]()
を得る。これを行列形式で表記すると
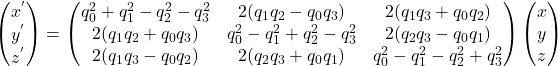
となる。拘束条件![]() を用いて書き直すと
を用いて書き直すと
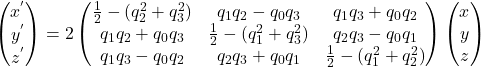
となる。この行列が論文内の式(10)である。4つの未知数に1つの拘束条件なので上の行列の自由度は3となる。3次空間内の回転の自由度は3なので矛盾はない。
まとめ
今回は、クォータニオンを用いた回転行列の表記について解説した。一番最後に示した行列が最近読んだ論文に出てきた式である。論文中では、ある目的を満たすように回転行列を最適化しているのであるが、クォータニオンを使うとその最適化が容易になるそうである。クォータニオンに関しては、3DCGをかじっていた頃に勉強したことがあるが、それ以来出会うことはなかった。今回改めて勉強し直したのでブログにまとめた。

