はじめに
最近、アメリカの女子高校生2人が、三角比を用いてピタゴラスの定理を証明したという記事を読んだ。三角比を用いた証明は既にいくつかあるが、「これまでに見た中で最も美しく、最も単純な証明である」と専門家が述べている。今回はこの証明を紹介する。使う道具は高校数学である。
一般的な証明
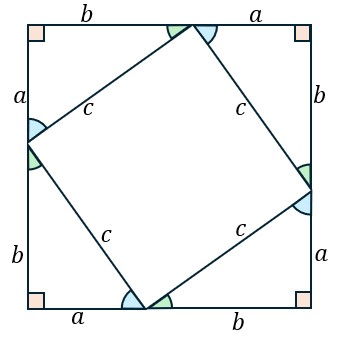
左のように直角三角形を4つ組み合わせ正方形を作る。この正方形の面積![]() は2通りの方法で書くことができる。
は2通りの方法で書くことができる。
![]()
これを変形すれば
![]()
を得る。これはピタゴラスの定理である。
三角比を用いた証明の難しさ
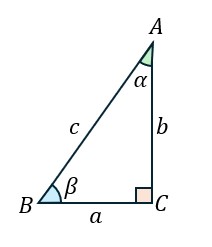
左のような直角三角形![]() を考える。ここで次の2つの三角比を考える。
を考える。ここで次の2つの三角比を考える。
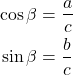
(1) ![]()
に2つの三角比を代入すると
![]()
を得る。両辺に![]() をかけると
をかけると
![]()
となる。これは求めたいピタゴラスの定理である。しかし、これは証明になっていない。公式(1)自体がピタゴラスの定理を前提としており、上の証明は循環論法になっているためである。
彼女たちの証明
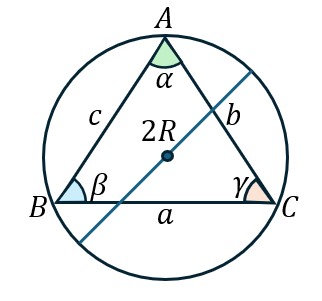
彼女たちは、公式(1)の代わりに次の正弦定理を用いた。
(2) ![]()
![]() は三角形
は三角形![]() の外接円の半径である。正弦定理は、ピタゴラスの定理を用いることなく証明することできる。ここではその証明は省略するので関心がある方はググってほしい。以下に三角比と正弦定理を用いたピタゴラスの定理の証明を示す。
の外接円の半径である。正弦定理は、ピタゴラスの定理を用いることなく証明することできる。ここではその証明は省略するので関心がある方はググってほしい。以下に三角比と正弦定理を用いたピタゴラスの定理の証明を示す。
まず最初に以下の図を考える。![]() であることに注意する。
であることに注意する。
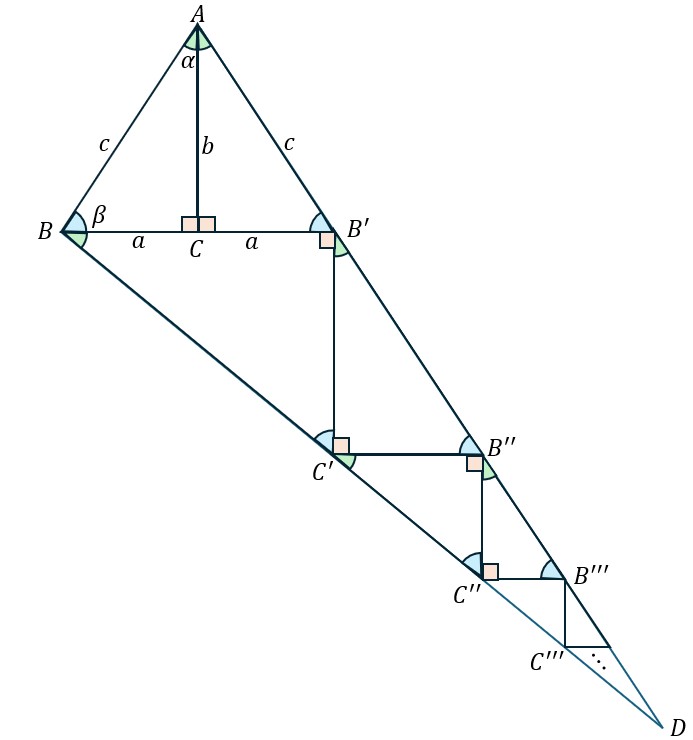
三角形![]() に注目して
に注目して
![]()
(3) ![]()
を得る。同じ三角形![]() について
について
![]()
となるから
![]()
となる。式(3)と![]() (三角形
(三角形![]() を参照)を代入して
を参照)を代入して
(4) ![]()
を得る。次に、三角形![]() に注目して
に注目して
![]()
式(4)と![]() を代入して
を代入して
(5) ![]()
を得る。同じ三角形![]() に対して
に対して
![]()
式(5)と![]() を代入して
を代入して
(6) ![]()
次に、三角形![]() に注目して
に注目して
![]()
式(6)と![]() を代入して
を代入して
(7) ![]()
同じ三角形![]() に対し
に対し
![]()
式(7)と![]() を代入して
を代入して
(8) ![]()
次に、三角形![]() に注目して
に注目して
![]()
式(8)と![]() を代入して
を代入して
(9) ![]()
を得る(そろそろ飽きてきた)。同じ計算を繰り返すと、線分![]() の長さは、式(3)、式(7)などを足したもの(等比級数の和)
の長さは、式(3)、式(7)などを足したもの(等比級数の和)
![]()
であり、線分![]() の長さは、
の長さは、![]() と式(5)、式(9)などを足したもの(初項以外は等比級数の和)になる。
と式(5)、式(9)などを足したもの(初項以外は等比級数の和)になる。
![]()
それぞれの無限級数の和を計算すると
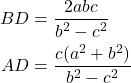
を得る。ここで三角形![]() に注目して正弦定理(やっと真打登場)を適用すると(角Bが直角であることに注意)
に注目して正弦定理(やっと真打登場)を適用すると(角Bが直角であることに注意)
(10) ![]()
ここで
![]()
であるから、式(10)の右側の等式にそれぞれの値を代入すると
![]()
これを変形すれば
![]()
を得る。これが求めたかったピタゴラスの定理である。
まとめ
今回は、三角比を用いたピタゴラスの定理の証明を紹介した。使っている道具は、三角比と正弦定理、無限等比級数の和だけであり、これらは高校数学で習う内容である。易しいけれど発想が素晴らしいと思う。今回は馬鹿正直に一つ一つ辺の長さを計算していったが本来であれば、「![]() 個目の三角形の三辺を計算せよ」のような設問に置き換えるべきだろう(数学的帰納法か?)。そのまま大学入試問題になりそうである。ところで、枯れた問題に対する新しい証明という文脈では他に、バーゼル問題に対しても最近新しい証明が提案された。これも高校数学の範囲で理解できる内容だ(ただし、かなりトリッキーな積分を繰り返す必要があるので易しくはない)。機会があればまた紹介したい。
個目の三角形の三辺を計算せよ」のような設問に置き換えるべきだろう(数学的帰納法か?)。そのまま大学入試問題になりそうである。ところで、枯れた問題に対する新しい証明という文脈では他に、バーゼル問題に対しても最近新しい証明が提案された。これも高校数学の範囲で理解できる内容だ(ただし、かなりトリッキーな積分を繰り返す必要があるので易しくはない)。機会があればまた紹介したい。

