はじめに
今回は、最適化問題を解く際に使われるラグランジュの未定乗数法について説明する。ラグランジュの未定乗数法とは、最適化したい関数とそれに付随する束縛条件から1つの式を作り、その式の極値を求める操作である。最初に、ラグランジュの未定乗数法で簡単な例題を解き、確かに極値が得られることを確認する。そのあとラグランジュの未定乗数法の仕組みを解説する。
ラグランジュの未定乗数法で極値を求める
以下の例題を考える(例題1)。
(1)
(2)
の極値を求めよ。
3次元空間に図示すると以下のようになる。束縛条件は円柱の側面(赤色)であり、関数![]() は放物曲面(緑色)である。
は放物曲面(緑色)である。
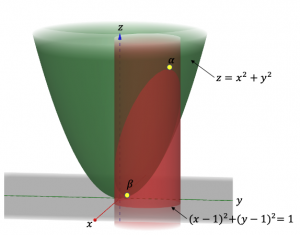
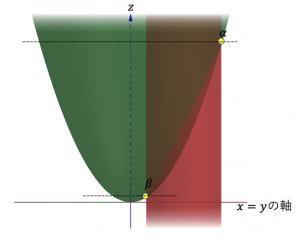
放物曲面と円柱の交線(楕円)上に存在する点のうち高さ![]() が一番大きい点(
が一番大きい点(![]() )と一番小さい点(
)と一番小さい点(![]() )が求めたい点である。前者は極大値、後者は極小値に相当する。
)が求めたい点である。前者は極大値、後者は極小値に相当する。
ラグランジュの未定乗数法ではまず最初に実数![]() を導入し、次の関数を考える。
を導入し、次の関数を考える。
(3) ![]()
右辺最初の2つの項は式(2)に対応し、第3項の括弧の中は、束縛条件(1)の右辺にある1を左辺に移行したものである。次に、![]() を
を![]() の関数とみなし極値を求める。
の関数とみなし極値を求める。
(4) 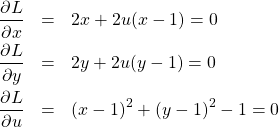
最初の2つの式から
(5) ![]()
(6) 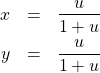
を得る。この2つの式を式(4)の3つ目の式に代入すると![]() についての2次方程式が得られる。これを解くと
についての2次方程式が得られる。これを解くと![]() を得る。式(6)の右辺に代入すると2組の
を得る。式(6)の右辺に代入すると2組の![]() を得る。
を得る。
(7) 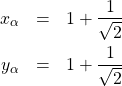
(8) 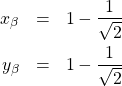
これら2つが極値を与える点の座標である。どちらが極大値であるかは実際に代入して確認する。今の場合![]() 、
、![]() となるので、
となるので、![]() が点
が点![]() (極大値)に、
(極大値)に、![]() が点
が点![]() (極小値)に対応する。
(極小値)に対応する。
実は、関数![]() から作られる次のヘッセ行列
から作られる次のヘッセ行列![]()
(9) 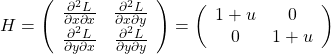
が正定値行列であれば極小値、負定値行列であれば極大値になると判定できるが、今回はこの理屈には深入りしない。興味ある方はこれやこれを見てほしい。
ラグランジュの未定乗数法のからくり
2次元ベクトルを![]() と書くことにすると、上の問題を以下のように一般化することができる(例題2)。
と書くことにすると、上の問題を以下のように一般化することができる(例題2)。
(10)
(11)
の極値を求めよ。
求めたい極値を![]() と書くことにする。式(10)より
と書くことにする。式(10)より
(12) ![]()
が成り立つ。![]() から微小量
から微小量![]() だけ動くと(
だけ動くと(![]() も2次元ベクトル)
も2次元ベクトル)
(13) ![]()
と近似できる(ここで、![]() は転置を表す)。
は転置を表す)。![]() の向きを
の向きを![]() と直交する向きに取ると(下図参照)
と直交する向きに取ると(下図参照)
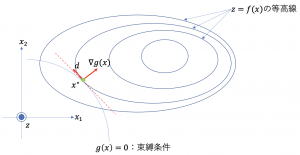
![]() なので
なので
(14) ![]()
となる。つまり、![]() と直交する方向に少し動いた点
と直交する方向に少し動いた点![]() でも束縛条件は成り立つ。次に、この点における
でも束縛条件は成り立つ。次に、この点における![]() の値を考える。同じように展開すると
の値を考える。同じように展開すると
(15) ![]()
を得る。いま、![]() と
と![]() の向きが直交していないとすると、
の向きが直交していないとすると、![]() は有限値を持つことになり
は有限値を持つことになり![]() が極値であるという仮定に反する。なぜなら、極値とはその近傍における最大値あるいは最小値のことだからである。従って、
が極値であるという仮定に反する。なぜなら、極値とはその近傍における最大値あるいは最小値のことだからである。従って、![]() と
と![]() は直交しなければならない。つまり、
は直交しなければならない。つまり、![]() が極値のとき、
が極値のとき、![]() と
と![]() の向きは平行でなければならない。つまり
の向きは平行でなければならない。つまり
(16) ![]()
を満たす実数![]() が存在するということである。いま、次の関数を定義する。
が存在するということである。いま、次の関数を定義する。
(17) ![]()
関数![]() をラグランジュ関数と呼ぶ。これを空間座標で微分しそれを0と置いたものが式(16)である。また、
をラグランジュ関数と呼ぶ。これを空間座標で微分しそれを0と置いたものが式(16)である。また、![]() で微分し0と置くと束縛条件
で微分し0と置くと束縛条件![]() を得る。つまり、例題2を解くことと、ラグランジュ関数の極値を求めることとは等価である。
を得る。つまり、例題2を解くことと、ラグランジュ関数の極値を求めることとは等価である。
今考えてきた![]() は2次元であるが、一般の
は2次元であるが、一般の![]() 次元に拡張することができる。さらに、複数の束縛条件に拡張することもできる。
次元に拡張することができる。さらに、複数の束縛条件に拡張することもできる。
(18) 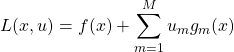
ここで、![]() 、
、![]() である。これら
である。これら![]() 個の変数について微分することにより極値を求めれば良い。以上が、ラグランジュの未定乗数法の理屈である。
個の変数について微分することにより極値を求めれば良い。以上が、ラグランジュの未定乗数法の理屈である。
まとめ
今回はラグランジュの未定乗数法について説明した。この手法で求まる複数の極値のうちどれが最適であるか(考える領域の中でどれが一番大きいか、あるいは一番小さいか)は別途確認する必要があることに注意しなければならない。
参考文献
補足
上の例題1は高校数学で解くことができる。束縛条件を円の極座標表示で表し![]() に代入すればよい。できますか?
に代入すればよい。できますか?

