はじめに
10年以上前になるが、某経済学者の本を読んでいると不思議な計算をしている場面に出くわした。彼曰く「軍事費を毎年5%ずつ増やしたとき現在の2倍になるのは70/5=14年後である」。70はどこから出てきたのか。今回はこれを確認する。
理屈
現在の予算を![]() とする。毎年
とする。毎年![]() %ずつ増額していき(
%ずつ増額していき(![]() )、
)、![]() 年後に2倍になるとする。このとき次式が成り立つ。
年後に2倍になるとする。このとき次式が成り立つ。
![]()
両辺を![]() で割ると
で割ると
![]()
(1) ![]()
左辺の対数を![]() が十分小さいとして
が十分小さいとして![]() の多項式で表したい。そこで次の無限級数を考える。
の多項式で表したい。そこで次の無限級数を考える。
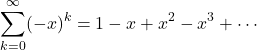
![]() なので上の無限級数は収束する。
なので上の無限級数は収束する。
![]()
この両辺を積分する。
![]()
これが式(1)の対数を![]() で展開した式である。
で展開した式である。![]() が十分小さいとき
が十分小さいとき
![]()
と書ける。したがって式(1)は
![]()
となる。これより
![]()
(2) ![]()
を得る。某経済学者の記事と同じ式である。この式が成り立つには、上の計算過程から明らかなように、![]() が1に比べて十分小さくなければならない。
が1に比べて十分小さくなければならない。
まとめ
今回は予算が2倍になるのに何年かかるのかを即座に計算できる式を紹介した。高校数学で理解できるものである。大手銀行の普通預金の金利は0.001%程度である。![]() を式(2)に代入すれば、資産が2倍になるのは何年後かがすぐわかります。そして悟ります。貯金が愚かな行為であることを(笑)。
を式(2)に代入すれば、資産が2倍になるのは何年後かがすぐわかります。そして悟ります。貯金が愚かな行為であることを(笑)。

