はじめに
今回は中心極限定理について説明する。数学的な証明は行わず、その振る舞いについてPythonプログラムで確認したあと、この定理の有用性の例を示す。
中心極限定理とは
任意の確率分布![]() を考える。その平均
を考える。その平均![]() と分散
と分散![]() は既知であるとする。この確率分布から独立に
は既知であるとする。この確率分布から独立に![]() 個のデータをサンプリングする。
個のデータをサンプリングする。
![]()
「独立に」とは、今のサンプリングが次のサンプリングに影響を与えないということである。このような![]() 個のサンプリングをたくさん繰り返す。
個のサンプリングをたくさん繰り返す。
![]()
各データの組![]() から平均(標本平均)を計算する。
から平均(標本平均)を計算する。
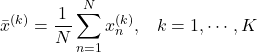
この平均の分布![]() は、
は、![]() を十分に大きくとると、平均が
を十分に大きくとると、平均が![]() 、分散が
、分散が![]() の正規分布に近づくことが証明されている。これが中心極限定理である。ここで大切なことは、最初に考えた確率分布
の正規分布に近づくことが証明されている。これが中心極限定理である。ここで大切なことは、最初に考えた確率分布![]() の種類は任意であることである。ベルヌーイ分布でも二項分布でも構わない。サンプリング数を十分大きくすればその平均は正規分布に近づくのである(下図参照)。
の種類は任意であることである。ベルヌーイ分布でも二項分布でも構わない。サンプリング数を十分大きくすればその平均は正規分布に近づくのである(下図参照)。

図1
Pythonによる実験
ここでは任意の確率分布として0以上1未満で定義された一様分布![]() を考える。
を考える。
![]()
このとき
![]()
が成り立ち、平均と分散は
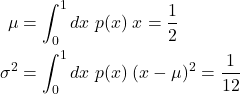
となる。さて、最初に以下の手順を実装する。
- 一様分布から
 個のデータを無作為に取り出す。
個のデータを無作為に取り出す。  個のデータの平均を計算する。
個のデータの平均を計算する。- 1と2を
 回繰り返す。
回繰り返す。
|
1 2 3 4 5 6 7 8 9 10 |
def calcuate_means(N: int, K: int) -> list[float]: x_means = [] for _ in range(K): xs = [] for n in range(N): x = np.random.rand() # 一様分布からの乱数生成 [0,1) xs.append(x) mean = np.mean(xs) # N個のサンプルの平均 x_means.append(mean) # K回繰り返す。 return x_means |
残りは、描画部分とメイン関数部分である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
def draw_graph(x_means: list[float], N: int, K: int, path: str, mu: float, sigma: float) -> None: plt.hist(x_means, bins="auto", density=True) plt.title(f"N={N}, K={K}") plt.xlabel("x") plt.ylabel("Probability Density") plt.xlim(-0.05, 1.05) plt.ylim(0, 5) # draw normal distribution x = np.linspace(-0.05, 1.05, 100) y = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-((x - mu) ** 2) / (2 * sigma**2)) plt.plot(x, y, color="red", linestyle="dashed") plt.savefig(path) plt.clf() def make_normal(mu: float, sigma: float): x = np.random.normal(mu, sigma) return x if __name__ == "__main__": K = 10000 MU = 0.5 SIGMA = np.sqrt(1.0 / 12.0) for n in [1, 2, 4, 10]: x_means = calcuate_means(n, K) path = f"outputs/pdf_{n:02d}.png" draw_graph(x_means, n, K, path, MU, SIGMA / np.sqrt(n)) |
特に難しい部分はない。実験結果は以下の図の通り。図内の![]() と
と![]() は上の説明で使用したパラメータに対応する。
は上の説明で使用したパラメータに対応する。![]() を10000に固定し、
を10000に固定し、![]() を増やしていく。青いヒストグラムは
を増やしていく。青いヒストグラムは![]() 個の
個の![]() (平均)の分布を表し、赤い点線はそれぞれの
(平均)の分布を表し、赤い点線はそれぞれの![]() のときの正規分布
のときの正規分布
![]()
である。
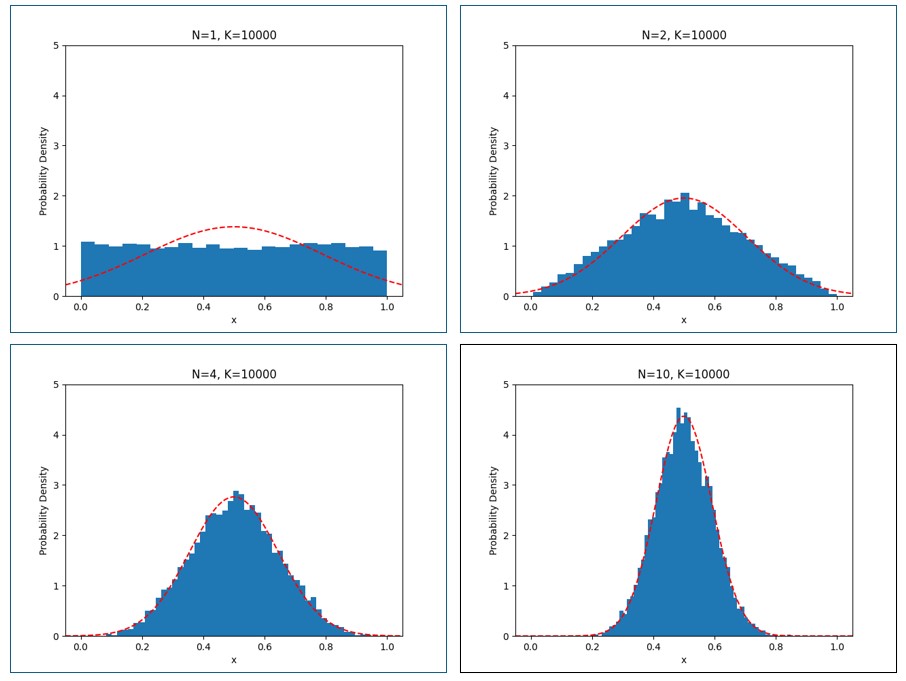
図2
![]() が大きいほど青いヒストグラムの分布は正規分布(赤い点線)に近づいていく様子が分かる。
が大きいほど青いヒストグラムの分布は正規分布(赤い点線)に近づいていく様子が分かる。![]() 程度でほぼ正規分布と一致している。今回使用したソースコードはここにある。
程度でほぼ正規分布と一致している。今回使用したソースコードはここにある。
中心極限定理はどこで役立つのか
ここまでの説明で中心極限定理については理解できたと思う。次にこれが役に立つ場面を紹介する。良く例に使われる日本人の身長について考えよう。日本人の身長を変数![]() 、その確率分布を
、その確率分布を![]() とおく。
とおく。![]() の真の形状は不明なので(全日本人の身長を測るわけにはいかない)、
の真の形状は不明なので(全日本人の身長を測るわけにはいかない)、![]() の平均と分散をそれぞれ
の平均と分散をそれぞれ![]() と
と![]() という未知数で与えておく。次に
という未知数で与えておく。次に![]() 人のサンプリングを行う。
人のサンプリングを行う。
![]()
これらの平均を計算し![]() を求める。このようなサンプリングから得られる平均は、中心極限定理によると次の正規分布
を求める。このようなサンプリングから得られる平均は、中心極限定理によると次の正規分布
![]()
に従うのであった。従って、正規分布の場合の区間推定を行うと、![]() は99.7%の確率で
は99.7%の確率で
(1) ![]()
を満たすと結論できる。今回は区間推定についての説明は割愛するが、例えば68–95–99.7則を見てほしい。この式を変形すると
![]()
を得る。さらに、統計学の教えるところによると、![]() が十分に大きい場合、真の分散
が十分に大きい場合、真の分散![]() はサンプリングデータから計算できる不偏分散
はサンプリングデータから計算できる不偏分散![]() に置き換えることができる(不偏分散については以前こちらの記事「標本分散と不偏分散」で解説した)。従って
に置き換えることができる(不偏分散については以前こちらの記事「標本分散と不偏分散」で解説した)。従って
(2) ![]()
を得る。上式において未知数は真の平均![]() だけである。すなわち、真の平均
だけである。すなわち、真の平均![]() を99.7%の確率で区間推定できたことになる。このような計算が可能なのは、中心極限定理により
を99.7%の確率で区間推定できたことになる。このような計算が可能なのは、中心極限定理により![]() が正規分布に従い、その結果、式(1)が成り立つためである。式(2)で
が正規分布に従い、その結果、式(1)が成り立つためである。式(2)で![]() にすると真の平均
にすると真の平均![]() が存在する区間が狭くなっていくことが分かる。
が存在する区間が狭くなっていくことが分かる。
まとめ
今回は中心極限定理について解説した。最近読んだ書籍「ゼロから作るDeep Learning 5」に中心極限定理が紹介されており、むかし勉強した知識を再度思い出すために今回の解説記事を書いた。中心極限定理が役立つ場面については自分で調べた内容を記載した。

