はじめに
今回は、最近の業務で使用したEarth Mover’s Distance(EMD)と呼ばれる量について解説する。これは2つの分布の間の距離尺度を与える量である。
問題設定
いま、運ぶ荷物![]() と、それを収める倉庫
と、それを収める倉庫![]() があるとする。
があるとする。![]() に対しては、荷物の場所(位置座標
に対しては、荷物の場所(位置座標![]() )と荷物量(
)と荷物量(![]() )が定義される。一方で、
)が定義される。一方で、![]() に対しては、倉庫の場所(位置座標
に対しては、倉庫の場所(位置座標![]() )と倉庫の容量(
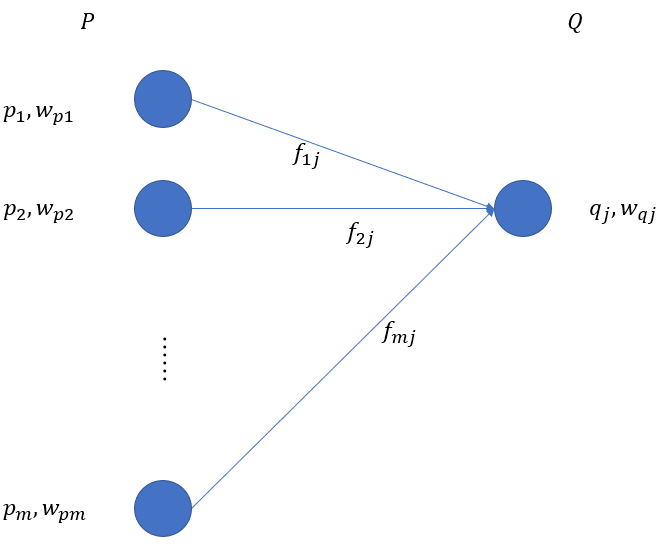
)と倉庫の容量(![]() )が定義される(下図参照)。
)が定義される(下図参照)。
(1) ![]()
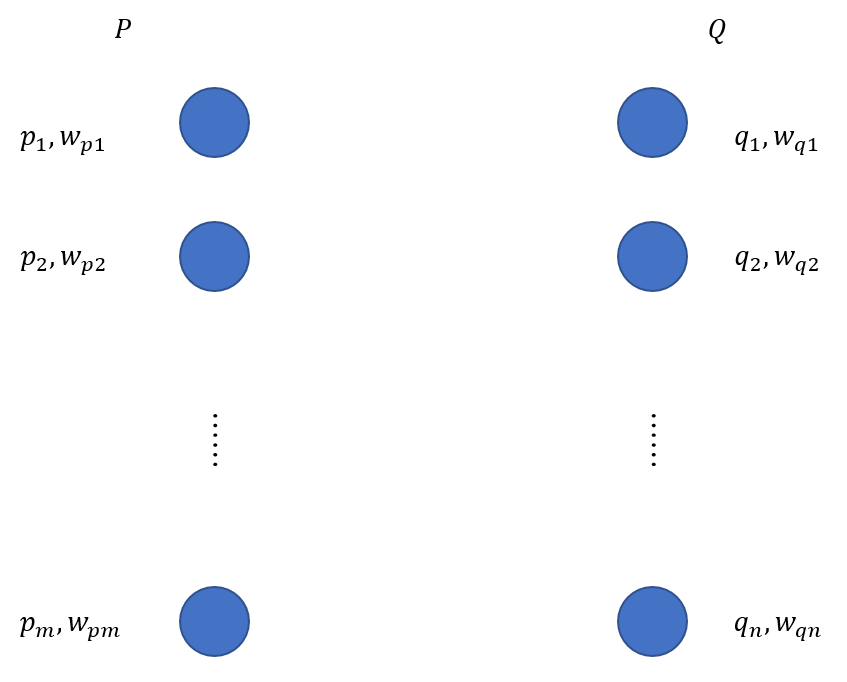
荷物![]() には
には![]() 個のサイトが、倉庫
個のサイトが、倉庫![]() には
には![]() 個のサイトが存在する。いま、
個のサイトが存在する。いま、![]() と
と![]() の間の距離
の間の距離![]() を考える。この距離
を考える。この距離![]() を用いて次の量を定義する。
を用いて次の量を定義する。
(2) 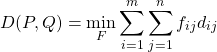
あらゆる![]() の組み合わせの中から2重和が最小となるものを見つけ、その最小値で
の組み合わせの中から2重和が最小となるものを見つけ、その最小値で![]() を定義するという意味である。ここで、
を定義するという意味である。ここで、![]() は、
は、![]() の
の![]() サイトから
サイトから![]() の
の![]() サイトへ移動する荷物の量を表し、これには複数の束縛条件が付く。まず最初に次を満たさなければならない。
サイトへ移動する荷物の量を表し、これには複数の束縛条件が付く。まず最初に次を満たさなければならない。
(3) ![]()
これは、荷物の移動は常に![]() から
から![]() の向きであり逆行することはないことを表す。さらに、次の束縛条件が付く。
の向きであり逆行することはないことを表す。さらに、次の束縛条件が付く。
(4) 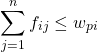
上式は、![]() の
の![]() サイトから
サイトから![]() のすべての倉庫へ移動する荷物量は、
のすべての倉庫へ移動する荷物量は、![]() の
の![]() サイトが持つ荷物量
サイトが持つ荷物量![]() を超えることはないことを表している(下図参照)。
を超えることはないことを表している(下図参照)。
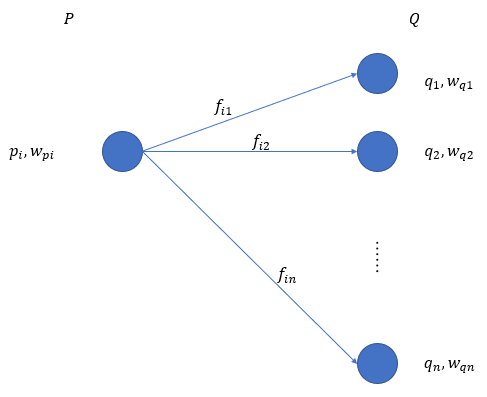
同様に、![]() の
の![]() サイトの倉庫が受け入れられる荷物量は
サイトの倉庫が受け入れられる荷物量は![]() を超えることはない(下図参照)。
を超えることはない(下図参照)。
(5) ![]()
最後に次の条件を課す。
(6) 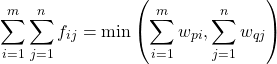
つまり、![]() と
と![]() の間で移動する荷物の総量は、
の間で移動する荷物の総量は、![]() の荷物の総量と
の荷物の総量と![]() の倉庫の総容量の小さいほうに等しい。これら4つの束縛条件の下で次式が最適化される(再掲)。
の倉庫の総容量の小さいほうに等しい。これら4つの束縛条件の下で次式が最適化される(再掲)。
(7) 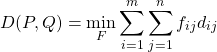
最適化された![]() を用いて次式を定義する。
を用いて次式を定義する。
(8) 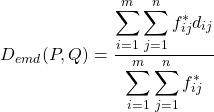
![]() がEarth Mover’s Distance(EMD)である。
がEarth Mover’s Distance(EMD)である。
適用例
画像処理では、2つの画像の類似度を見る際にEMDが用いられることがある。今回はこの適用例を紹介する。下の4つの画像を考える。

カッコ内には画像の幅・高さと色の数が記載してある。これらの画像は通常のRGB画像とは異なり、色数が制限されている。例えば、sea_1という画像の(R,G,B)の組の数は78個である。つまり、78個の色で表現された画像ということになる。画像sea_1の場合、画素数は![]() である。そして、各画素には78個の色のうちどれかひとつだけが割り振られている。各色がいくつの画素に割り振られているかを勘定するとヒストグラムを得ることができる(下図参照)。
である。そして、各画素には78個の色のうちどれかひとつだけが割り振られている。各色がいくつの画素に割り振られているかを勘定するとヒストグラムを得ることができる(下図参照)。
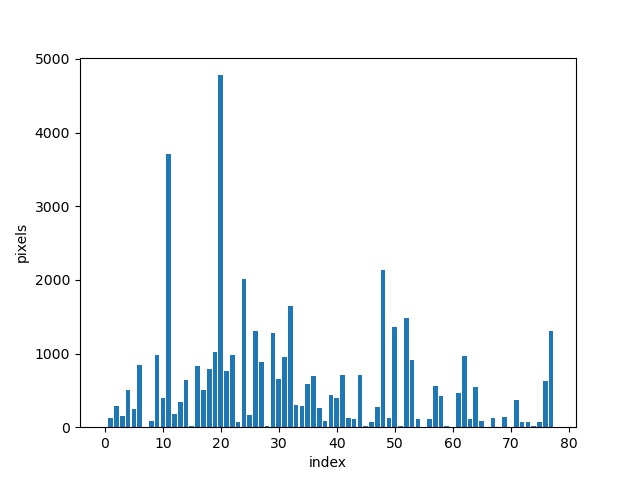
横軸は各色に適当に番号を付けたもの、縦軸は各色に属する画素数である。このヒストグラムは画像sea_1の特徴を表現する分布とみなすことができる。そして、色の値![]() を座標値、その色に属する画素数を荷物量/倉庫の容量とみなせばEMDを用いて2つの画像間の距離を計算することができることに気付くだろう。計算コードはここにある(C++言語で実装した)。残念ならがPythonで利用できるEMDを計算するライブラリは見当たらなかったので、こちらのC言語で実装されたコードを利用した。各ペア間のEMDの値を以下に示す。
を座標値、その色に属する画素数を荷物量/倉庫の容量とみなせばEMDを用いて2つの画像間の距離を計算することができることに気付くだろう。計算コードはここにある(C++言語で実装した)。残念ならがPythonで利用できるEMDを計算するライブラリは見当たらなかったので、こちらのC言語で実装されたコードを利用した。各ペア間のEMDの値を以下に示す。
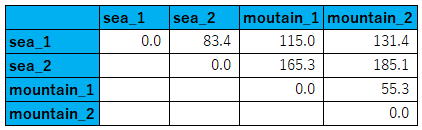
海同士の画像や山同士の画像の間の距離の方が、海と山の画像間の距離よりも小さいことが分かる。
まとめ
今回は、2つの分布間の距離を表すEarth Mover’s Distance(EMD)を紹介した。これは、複数の束縛条件の下で最適化される距離である。束縛条件を少し変えれば、あるPythonライブラリを使うことができるが、一般的なEMDとは異なってしまうのでC言語のコードを利用した。
ところで、なぜEarth Move’s Distanceと呼ぶのだろうか?私の推測だが、ここで使われるEarthは「地球」ではなく「土」や「土量」を意味すると思われる。ある場所の土を別の場所に移す際の労力を測る尺度という意味でEarth Mover’s Distanceという名前が付いたのではなかろうか。

