はじめに
先日、数学系Youtubeを見ていたら面白い問題を扱っていたので紹介する。
問題
任意の2つの自然数が互いに素である確率を求めよ。
問題文はシンプルだが、ゼータ関数のオイラー積表示やバーゼル問題が顔を出す大変興味深い問題である。
解答
ある自然数を考えたとき、それが![]() の倍数である確率は
の倍数である確率は![]() である。例えば、ある自然数が2の倍数となる確率は
である。例えば、ある自然数が2の倍数となる確率は![]() 、3の倍数となる確率は
、3の倍数となる確率は![]() である。いま、2つの自然数
である。いま、2つの自然数![]() を取り出したとき、それらが同時に
を取り出したとき、それらが同時に![]() の倍数にならない確率
の倍数にならない確率![]() は、同時に
は、同時に![]() の倍数になる確率を1から引けばよいので
の倍数になる確率を1から引けばよいので
(1) ![]()
(2) ![]()
と書くことができる。ここで、![]() は素数である。すなわち、
は素数である。すなわち、![]() が互いに素になるとは、「同時に2の倍数にならない」かつ「同時に3の倍数にならない」かつ「同時に5の倍数にならない」…ということである。このことを、もう少し具体的に見てみる。いま、
が互いに素になるとは、「同時に2の倍数にならない」かつ「同時に3の倍数にならない」かつ「同時に5の倍数にならない」…ということである。このことを、もう少し具体的に見てみる。いま、![]() とする。それぞれを素因数分解すると、
とする。それぞれを素因数分解すると、![]() である。
である。![]() が同時に
が同時に![]() の倍数になることはなく、
の倍数になることはなく、![]() の倍数になることもなく、
の倍数になることもなく、![]() の倍数になることもなく、
の倍数になることもなく、![]() の倍数になることもない。従って、
の倍数になることもない。従って、![]() は互いに素である。
は互いに素である。
式(2)の計算をさらに進める。
(3) 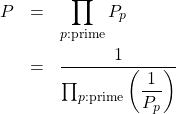
この分母を考える。
(4) 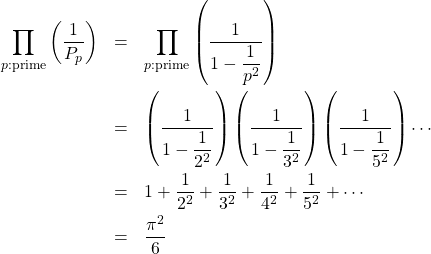
上式右辺の2行目から3行目への変形にゼータ関数のオイラー積表示を用いている。また、3行目から4行目への変形はバーゼル問題と呼ばれる計算である。この結果を式(3)に代入すれば
(5) ![]()
を得る。これが、任意の2つの自然数が互いに素になる確率である。数値で表してみると0.60792…となるので、0.5よりは大きいことが分かる。
補足
(6) 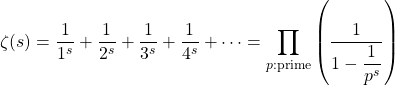
関数![]() はゼータ関数と呼ばれ、複素数
はゼータ関数と呼ばれ、複素数![]() で定義された関数である。上で用いた変形は
で定義された関数である。上で用いた変形は![]() の場合である。式(6)の証明は割と簡単に行うことができる。簡単のため、
の場合である。式(6)の証明は割と簡単に行うことができる。簡単のため、![]() の場合を考える。
の場合を考える。
(7) ![]()
分母に現れる数を素因数分解して書くと
(8) 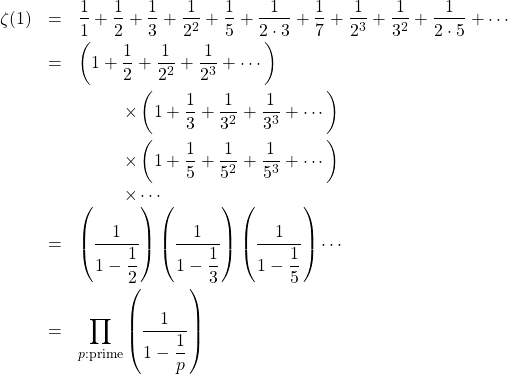
となる。一般の![]() の場合も同様である。
の場合も同様である。
一方、バーゼル問題とは次式のことである。
(9) ![]()
この式の証明は長くなるので割愛する。興味があればググってほしい。バーゼルとは、この問題を解いたオイラーの故郷の名である。
まとめ
今回は興味深い問題を紹介した。問題はシンプルであるが、その解答には
が現れる。また、ゼータ関数のオイラー積表示からは、素数とゼータ関数の間の親密な関係も垣間見ることができる。

