はじめに
今回は、Variational Auto Encoder（VAE）を外れ値検知に応用した例を示し、その可能性について議論したい。
Variational Auto Encoderとは
詳細な理論はこことここで述べたので、今回は概略だけを示す。
観測値
が与えられとき、未観測の値
を生成する確率分布
を求めたい。これを求めるためBayes推論で使われる変分推論（Variational Inference）を用いると、以下のような処理の流れを得る。
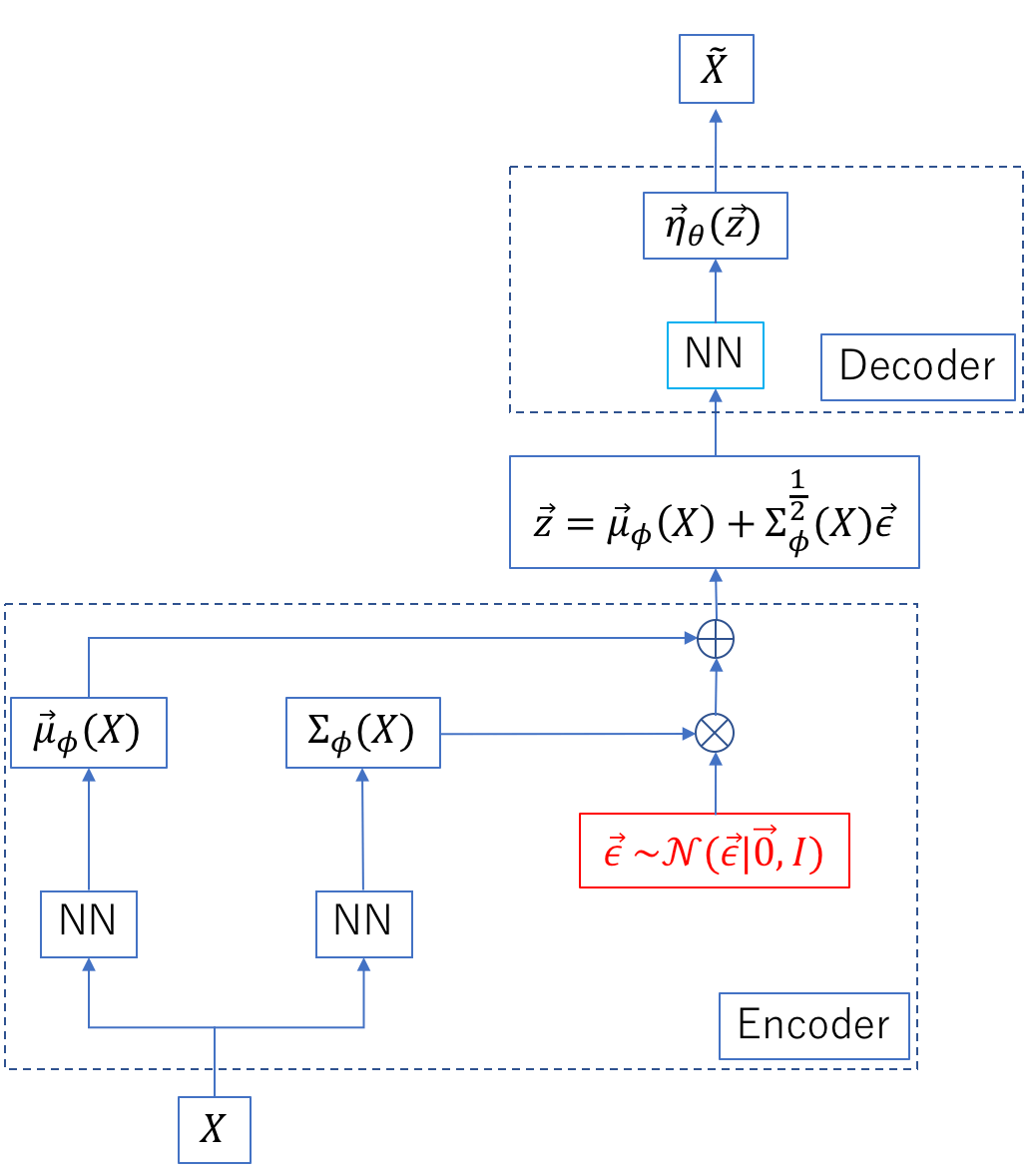
図の「NN」はニューラルネットワークを表す。また、標準正規分布からサンプリングしている部分を赤で示した。入力
を隠れ変数
に射影し（Encoder）、からを復号する（Decoder）構造を持つ。復号されたを
と記した。この処理の流れをVariational Auto Encoder（VAE）と呼ぶ。「Variational」は変分推論の「変分」から来た言葉である。
Encoder側の２つのNNでパラメータ
と
を計算する。後者は行列である。これらは正規分布のパラメータである。一方、Decoder側のNNではパラメータ
を算出する。これはモデル尤度（確率分布）のパラメータに相当する。EncoderとDecoderの２つを含む全手順を最適化する損失関数には、を0に、
を単位行列に近づけるような正則化項が含まれるので、の分布は標準正規分布に近い形状となる。すなわち、任意の変数がほぼ標準正規分布に従う確率変数に射影されることになる。これとよく似た手法としてAuto Encoderがあるが、収斂進化のようなものであり、理論的背景は別物である。
外れ値検知の問題設定
今回取り上げるデータセットは、MNISTである。MNISTは下図に示すような手書き数字の画像を集めたものである(下図はhttp://ainow.ai/2017/03/29/110012/から引用した）。
これらの数字の内、「0」を正常データ、「6」を外れ値データとみなす。正常データだけでVAEを訓練し、この訓練済みモデルで外れ値を検出できるか否かを検証する。
ソースコード
今回のコードはここにある。
訓練
6万枚の全画像の中に「0」画像は6903枚ある。この内、5923枚を訓練データ、残りをテストデータとした。mnistの画像はグレイ画像である。今回のVAEの実装では、Decoderの部分に、２値画像を想定したBernoulli分布を用いている。従って、あらかじめ、全画像を２値に変換する処理を行った（make_binarized_mnist.py）。そのあと、train_vae_with_specified_label.pyで訓練を行った。また、ネットワーク構造はnet_2.pyに記載されている。の次元数を
、
、
とした。=100、エポック数を100として訓練を行ったときの損失関数の学習曲線を以下に示す。描画時に使用したファイルは、draw_results_with_specified_label.ipynbである。
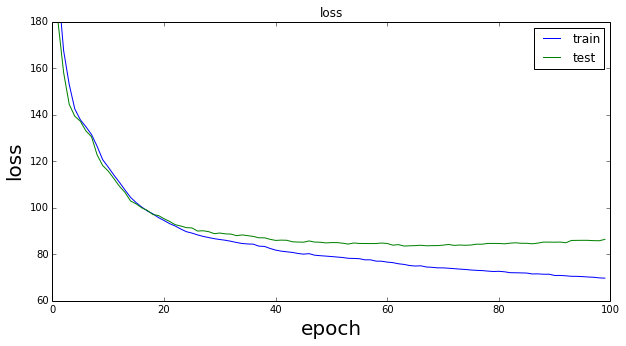
訓練後のとのそれぞれの全要素の平均値は以下のようになる。
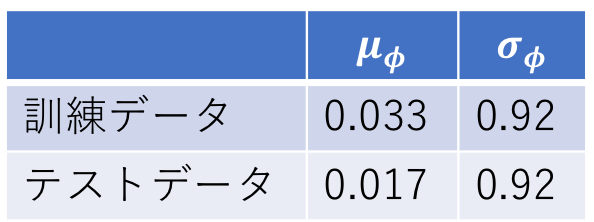
先に説明したように、
は0に近い値に、
は1に近い値となっていることが分かる。すなわち、近似的に標準正規分布に従う隠れ変数が得られたことになる。
データの分布
訓練済みモデルのEncoder部分を用いて、正常画像（0画像）と外れ値画像（6画像）を隠れ変数に変換した結果が下図である。ただし、t-SNEを用いて100次元を2次元に削減した。正常画像は1000枚、外れ値画像は100枚である。
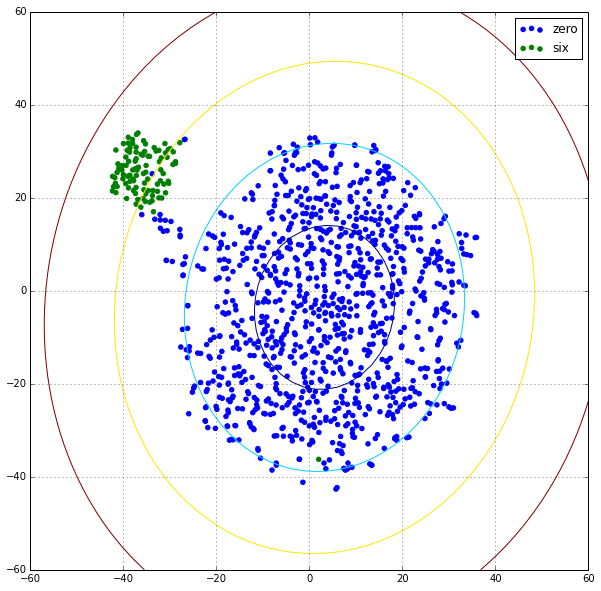
図の楕円は、Mahalanobis距離の等高線である。内側から1,2,3,4の値を持つ。
しきい値の決定
はほぼ正規分布に従う変数であるから、Mahalanobis距離を用いてしきい値を決定すれば良い。しきい値と各種指標の関係を以下に示す（detect_anomaly.py）。
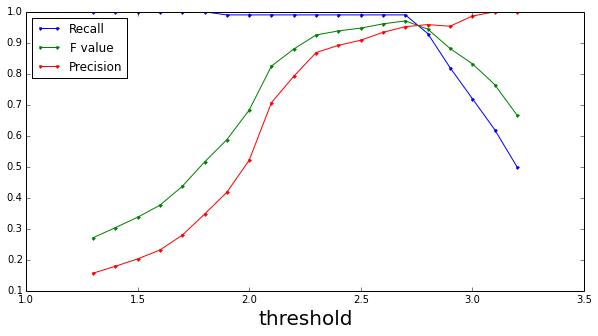
F値はthresholdが2.7のとき最大値0.97となる。このときのPrecisionとRecallの値はそれぞれ0.95と0.99である。
まとめ
今回は、VAEによる外れ値検知の可能性を探った。正常データで訓練されたVAEのEncoderは正常データを標準正規分布に従う変数に変換する。一方、訓練時に使用しなかった異常データはこの分布から外れた場所に射影されると期待される。この識別はMahalanobis距離を用いれば容易に実現できることを示した。
隠れ変数の次元を今回は100とした。最適な次元数については時間をかけてもう少し検討した方が良い。これは今後の課題である。また、しきい値を決定する際に2次元に次元を圧縮したが、これについてもまだ検討の余地はある。
