こんにちはtetsuです。
今回はPyTorchの入門的な記事となります。PyTorchを使ったディープラーニングのサンプルコードはよくありますが、それとは別の方法で説明していきたいと思います。PyTorchでおこなう処理の流れはディープラーニングを扱う場合と変わりませんので、計算の本質的な部分はある程度この記事で理解できるようになることを目指します。
PyTorchを使って解きたい問題、解き方
問題設定
今回は
![]()
に対して![]() となるような
となるような![]() を求める問題を解いていこうと思います。この問題の答えは手計算によってすぐに求まり、
を求める問題を解いていこうと思います。この問題の答えは手計算によってすぐに求まり、
![]()
となりますね。簡単すぎるかもしれませんが、答えが分かっている問題を解いたほうが計算が追いやすく、理解の手助けになるかなと思います。
解き方
先程設定した問題では手計算ですぐに答えが求まるので、次から説明することは回りくどく思うかもしれませんが、ディープラーニングのライブラリの計算方法を理解する上で必要な話になります。
ディープラーニングでは勾配降下法という手法をベースにしたものを使って解を求めていきます。
この勾配降下法を使う際には損失関数というものを定義する必要があります。損失関数をより小さくすることができる![]() が見つかったとき、より良い答え(
が見つかったとき、より良い答え(![]() により近い
により近い![]() )が求まる、というような観点で損失関数を設計します(機械学習においては過学習の話を出すとこの限りではありませんが、置いておきましょう)。今の問題で考えると、
)が求まる、というような観点で損失関数を設計します(機械学習においては過学習の話を出すとこの限りではありませんが、置いておきましょう)。今の問題で考えると、![]() と
と![]() との差が小さくなる
との差が小さくなる![]() を求めたいので、例えば次のような損失関数
を求めたいので、例えば次のような損失関数![]() を最小化できれば良さそうです。
を最小化できれば良さそうです。
![]()
この損失関数をグラフにしておきます。赤丸はそれぞれ![]() をあらわします。
をあらわします。
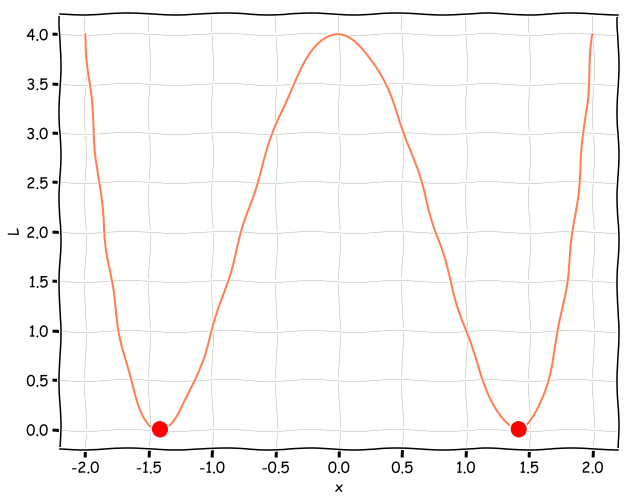
勾配降下法では損失関数![]() を微分することで勾配を求めます。今回の場合には勾配は次式であらわされます。
を微分することで勾配を求めます。今回の場合には勾配は次式であらわされます。
(1) ![]()
実はこの勾配にマイナスを掛けた方向に![]() を移動させることで、
を移動させることで、![]() を小さくすることができます。そのため、次式のように
を小さくすることができます。そのため、次式のように![]() を移動させます。
を移動させます。
(2) ![]()
ここで![]() は学習率と呼ばれるもので、どれだけ
は学習率と呼ばれるもので、どれだけ![]() を動かすかを制御する値になります。学習率が大きければ、
を動かすかを制御する値になります。学習率が大きければ、![]() は大きく移動することになります。大きすぎると移動しすぎる可能性もありますが、小さすぎるとほとんど移動しないため、いい塩梅の値を見つける必要があります。
は大きく移動することになります。大きすぎると移動しすぎる可能性もありますが、小さすぎるとほとんど移動しないため、いい塩梅の値を見つける必要があります。
ここまで説明したような①「勾配を求める」②「![]() を移動」という2つの操作を繰り返すことで、
を移動」という2つの操作を繰り返すことで、![]() を小さくする方向に少しずつ
を小さくする方向に少しずつ![]() を移動させていきます。残念ながら勾配降下法では一回で答えが求まるわけではなく、ちょっとずつ答えに近づけていきますが、この方法によって、人間の手計算が困難な場合でも最小値あるいは極小値をとる
を移動させていきます。残念ながら勾配降下法では一回で答えが求まるわけではなく、ちょっとずつ答えに近づけていきますが、この方法によって、人間の手計算が困難な場合でも最小値あるいは極小値をとる![]() の近似値を求めることができます。
の近似値を求めることができます。
PyTorchのコードと説明
ここまでに説明した解き方をPyTorchを用いたプログラムにしたものが以下です。なおPyTorchのバージョンは1.0を想定しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import torch import torch.nn as nn import torch.optim as optim x = torch.tensor([1.], requires_grad=True) loss_func = nn.MSELoss() optimizer = optim.SGD([x], lr=0.01) target = torch.tensor([0.]) for iter_num in range(100): optimizer.zero_grad() y = x ** 2 - 2 loss = loss_func(y, target) loss.backward() print("{0}: x={1:.7f}, y={2:.7f}, dL/dx={3:.7f}".format(iter_num, x.data.numpy()[0], y.data.numpy()[0], x.grad.data.numpy()[0])) optimizer.step() print("x={0:.7f}".format(x.data.numpy()[0])) |
プログラムの内容について確認していきます。
- 5行目で
 の初期値を決めていきます。今回は
の初期値を決めていきます。今回は としています。勾配降下法では損失関数が小さくなるように
としています。勾配降下法では損失関数が小さくなるように が動いていくので、初期値の都合上、ひたすら
が動いていくので、初期値の都合上、ひたすら の方向へ向かっていきます。先程示した損失関数のグラフをみても分かるとおり、
の方向へ向かっていきます。先程示した損失関数のグラフをみても分かるとおり、 から
から へ移動するには一度損失関数の値が大きくなる必要があるため、
へ移動するには一度損失関数の値が大きくなる必要があるため、 の近くには辿り着きません。またrequires_grad=Trueは
の近くには辿り着きません。またrequires_grad=Trueは を計算させるという意味になります。
を計算させるという意味になります。 - 6行目のloss_func = nn.MSELoss()では損失関数を選択しています。MSELossは解き方のところで出てきた損失関数と同じ役割を担います。
- 7行目のoptimizer = optim.SGD([x], lr=0.01)では
 を移動させる方法としてSGDを選んでいます。SGDは確率的勾配降下法と呼ばれ、説明した解き方と同じ働きをします。lr=0.01では学習率を0.01と定義しています。[x]の部分はSGDで移動させていく変数になります。ディープラーニングではここに指定する変数がたくさん出てきますが、今回は
を移動させる方法としてSGDを選んでいます。SGDは確率的勾配降下法と呼ばれ、説明した解き方と同じ働きをします。lr=0.01では学習率を0.01と定義しています。[x]の部分はSGDで移動させていく変数になります。ディープラーニングではここに指定する変数がたくさん出てきますが、今回は のみです。
のみです。 - 11行目では勾配の計算結果を0で初期化しています。13行目で損失関数の値を計算し、それを利用して14行目で勾配を計算しているのですが、内部的には「(
 の勾配)
の勾配)  」というように、代入ではなく加算がおこなわれます。このため、11行目の処理で一旦勾配の値の初期化が必要となります。
」というように、代入ではなく加算がおこなわれます。このため、11行目の処理で一旦勾配の値の初期化が必要となります。 - 16行目では計算した勾配を用いて
 の移動をおこなっています。
の移動をおこなっています。
このプログラムは勾配降下法の各反復ごとの![]() とそのときの
とそのときの![]() 、
、![]() の値を標準出力しており、実行してみると次のように表示されます。一番上の行は初期値の
の値を標準出力しており、実行してみると次のように表示されます。一番上の行は初期値の![]() で計算した値であることに注意して下さい。
で計算した値であることに注意して下さい。
|
1 2 3 4 5 6 7 8 |
0: x=1.0000000, y=-1.0000000, dL/dx=-4.0000000 1: x=1.0400000, y=-0.9184000, dL/dx=-3.8205440 2: x=1.0782053, y=-0.8374733, dL/dx=-3.6118727 ︙ (省略) ︙ 99: x=1.4142133, y=-0.0000007, dL/dx=-0.0000040 x=1.4142133 |
初期値に対応する勾配![]() ですが、これは式(1)を用いて
ですが、これは式(1)を用いて
![]()
と計算したものと等しいことが確認できます。
またその次の行での![]() は
は![]() ですが、式(2)を用いて
ですが、式(2)を用いて
![]()
と計算したものと等しいことが確認できます。
100反復後には![]() ですので、おおよそ
ですので、おおよそ![]() となっていることが確認できます。単精度で計算していますので、精度はこの程度が限界です。
となっていることが確認できます。単精度で計算していますので、精度はこの程度が限界です。
終わりに
今回は簡単な方程式をPyTorchを使って解かせる例を示しました。ディープラーニングを用いたコードも似たような流れで処理をおこないますので、導入として参考になれば幸いです。

