はじめに
今回は、先に示したChainerによるLSTMの実装を、chainer.links.NStepLSTMを用いて書き換える。さらに、GPU上でも動作する仕組みを導入し、CPU上との速度比較を行う。
実行環境
GPU環境
- Amazon EC2 g2.2xlarge
- OS: Ubuntu 16.04.1 LTS
- CPU: Intel(R) Xeon(R) CPU E5-2650 v2 @ 2.60GHz
- Core数: 8
- Memory: 15GiB
- GPU: Tesla GRID K520搭載(video memory 4GB)
- Python: Python 3.4.3
- Chainer version: 3.0.0
CPU環境
- MacBook Pro (15-inch, Late 2016)
- OS: macOS Sierra
- CPU: 2.9GHz Intel Core i7
- Core数: 4
- Memory: 16GB
- Python: anaconda3-5.0.0 (Python 3.6.2)
- Chainer version: 3.0.0
全ソース
今回用いたソースはこちらに置いてある。
NStepLSTM
NStepLSTMはChainer1.16.0からサポートされているクラスである。従来のLSTM(chainer.links.LSTM)との違いは以下の通りである。
- 先のLSTMの解説で
 と置いたもの(シーケンス長)を可変長にできる。
と置いたもの(シーケンス長)を可変長にできる。 - cuDNNを用いて最適化されているので、chainer.links.LSTMと比べ高速である。
- LSTMの多層化を引数ひとつで実現できる。
chainer.links.LSTMとchainer.links.NStepLSTMのインターフェースを次に示す。
|
1 2 3 |
# chainer.links.LSTMのインターフェース def __init__(self, in_size, out_size=None, lateral_init=None, upward_init=None, bias_init=None, forget_bias_init=None): def __call__(self, x): |
|
1 2 3 |
# chainer.links.NStepLSTMのインターフェース def __init__(self, n_layers, in_size, out_size, dropout, initialW=None, initial_bias=None, **kwargs): def __call__(self, hx, cx, xs, **kwargs): |
これらの間の大きな違いは以下の通りである。
- NStepLSTM.__init__の第1引数n_layersにLSTM層の数を指定する。
- NStepLSTM.__call__に隠れ層の初期状態(hx)とセルの初期状態(cx)を渡す必要がある。
- NStepLSTM.__call__の第4引数xsは、(seq_size,n_in)のサイズを持つtupleの配列である。ここでseq_sizeはひとつのシーケンスの長さ(
 )、n_inは入力データの次元である。配列の要素数はバッチサイズに相当する。
)、n_inは入力データの次元である。配列の要素数はバッチサイズに相当する。
LSTM.__call__に渡すxとNStepLSTM.__call__に渡すxsとの違いを以下に図で示す。
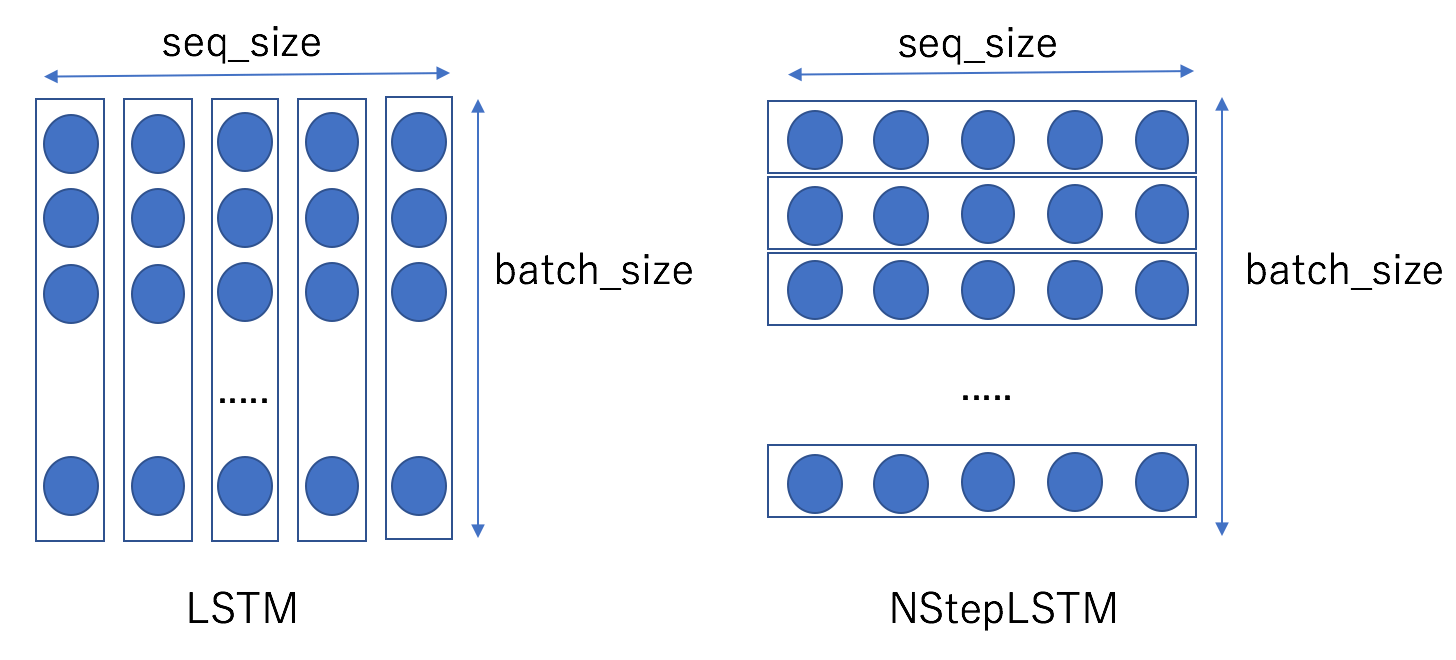
LSTMの場合(左図)、矩形で囲んだ各列を左から右に向かって順にxに渡していく。一方、NStepLSTMの場合(右図)は、矩形で囲んだ各行を上から順に配列に納めてxsに渡し一括処理を行う。今回示す例ではseq_sizeを固定長(=![]() )とするが、このサイズを可変長にできるのがNStepLSTMの利点である。
)とするが、このサイズを可変長にできるのがNStepLSTMの利点である。
chainer.links.LSTMに似たインタフェースとするため、以下のクラス(nstep_lstm/nstep_lstm.py)を定義する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
#!/usr/bin/env python # -*- coding: utf-8 -*- from params import * # noqa import chainer.links as L import chainer.functions as F import chainer import numpy as np import random # https://qiita.com/chantera/items/d8104012c80e3ea96df7 xp = np if GPU >= 0: xp = chainer.cuda.cupy # always run the same calculation np.random.seed(SEED) print('use gpu') else: print('use cpu') # always run the same calculation xp.random.seed(SEED) random.seed(SEED) class LSTM(L.NStepLSTM): def __init__(self, n_layers, in_size, out_size, dropout=0.5, initialW=None, initial_bias=None, **kwargs): super(LSTM, self).__init__(n_layers, in_size, out_size, dropout, initialW, initial_bias, **kwargs) with self.init_scope(): self.reset_state() def __call__(self, xs): hy, cy, ys = super(LSTM, self).__call__(self.hx, self.cx, xs) self.hx = hy self.cx = cy return ys def reset_state(self): self.hx = None self.cx = None def to_cpu(self): super(LSTM, self).to_cpu() if self.cx is not None: self.cx.to_cpu() if self.hx is not None: self.hx.to_cpu() def to_gpu(self, device=None): super(LSTM, self).to_gpu(device) if self.cx is not None: self.cx.to_gpu(device) if self.hx is not None: self.hx.to_gpu(device) |
- hx,cxの値は明示的に与えず、デフォルト値(全要素が0の配列)を利用する。
- to_cpuとto_gpuはCPU/GPU上の計算をサポートするための仮想関数である。オーバライドする。
- 常に同じ結果が得られるように、16,22,23行目にあるseed関数で乱数値を固定する。
- 12行目から19行目の記述でGPU/CPUを切り替えている。
定数SEED,GPUは以下のnstep_lstm/params.py内で定義される。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
#!/usr/bin/env python # -*- coding: utf-8 -*- # LSTM層の数 N_LAYERS = 2 DROPOUT = 0.3 # fibonacci数列を割る値 VALUE = 5 # 時系列データの全長 TOTAL_SIZE = 2000 # 訓練とテストの分割比 SPRIT_RATE = 0.9 # 入力時の時系列データ長 SEQUENCE_SIZE = 30 EPOCHS = 60 BATCH_SIZE = 100 # 入力層の次元 N_IN = 1 # 隠れ層の次元 N_HIDDEN = 200 # 出力層の次元 N_OUT = 1 GPU = 0 SEED = 0 |
GPU上で計算するときはGPU=0(デバイス番号)、CPU上で計算するときはGPU=-1(任意の負の値)とすれば良い。前者の場合はcupyが、後者の場合はnumpyが使われる。
訓練コード
上で定義したクラスLSTMを用いた訓練時のコードを以下に示す(nstep_lstm/nstep_lstm_using_chainer_with_fibonacci.py)。以前のコードとほぼ同じである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |
#!/usr/bin/env python # -*- coding: utf-8 -*- from params import * # noqa import chainer from chainer import optimizers import chainer.links as L import chainer.functions as F import numpy as np from chainer import serializers import _pickle import nstep_lstm # https://qiita.com/aonotas/items/8e38693fb517e4e90535 # https://qiita.com/TokyoMickey/items/cc8cd43545f2656b1cbd xp = np if GPU >= 0: xp = chainer.cuda.cupy # LSTM class MyNet(chainer.Chain): def __init__(self, n_layers=1, n_in=1, n_hidden=20, n_out=1, dropout=0.5, train=True): super(MyNet, self).__init__() with self.init_scope(): self.l1 = nstep_lstm.LSTM(n_layers, n_in, n_hidden, dropout) self.l2 = L.Linear(n_hidden, n_out, initialW=chainer.initializers.Normal(scale=0.01)) self.train = train def __call__(self, x): # x.shape: [(seq_size, n_in)] * batch_size h = self.l1(x) # [(seq_size, n_hidden)] * batch_size h = F.concat(h, axis=0) # [seq_size * batch_size, n_hidden] y = self.l2(h) # [seq_size * batch_size, n_out] return y def reset_state(self): self.l1.reset_state() # 損失値計算器 class LossCalculator(chainer.Chain): def __init__(self, model): super(LossCalculator, self).__init__() with self.init_scope(): self.model = model # x.shape: [(seq_size, n_in)] * batch_size # t.shape: [(seq_size, n_out)] * batch_size def __call__(self, x, t): y = self.model(x) # [seq_size * batch_size, n_out] assert y.shape == (SEQUENCE_SIZE * BATCH_SIZE, N_OUT) t = F.concat(t, axis=0) # [seq_size * batch_size, n_out] assert t.shape == (SEQUENCE_SIZE * BATCH_SIZE, N_OUT) loss = F.mean_squared_error(y, t) return loss # バッチ単位で1つのシーケンスを学習する。 def calculate_loss(model, seq): batch_size, cols = seq.shape assert cols - 1 == SEQUENCE_SIZE xs = [] ts = [] for row in seq: x = row[:-1].reshape(cols - 1, N_IN) t = row[1:].reshape(cols - 1, N_OUT) assert x.shape == (SEQUENCE_SIZE, N_IN) assert t.shape == (SEQUENCE_SIZE, N_OUT) xs.append(chainer.Variable(x.astype(dtype=xp.float32))) ts.append(chainer.Variable(t.astype(dtype=xp.float32))) loss = model(xs, ts) return loss # モデルを更新する。 def update_model(model, seq): loss = calculate_loss(model, seq) # 誤差逆伝播 loss_calculator.cleargrads() loss.backward() # バッチ単位で古い記憶を削除し、計算コストを削減する。 loss.unchain_backward() # バッチ単位で更新する。 optimizer.update() return loss # Fibonacci数列から周期関数を作る。 class DatasetMaker(object): @staticmethod def make(total_size, value): return (DatasetMaker.fibonacci(total_size) % value).astype(np.float32) # 全データを入力時のシーケンスに分割する。 @staticmethod def make_sequences(data, seq_size): data_size = len(data) row = data_size - seq_size seqs = xp.ndarray((row, seq_size)).astype(xp.float32) for i in range(row): seqs[i, :] = data[i: i + seq_size] return seqs @staticmethod def fibonacci(size): values = [1, 1] for _ in range(size - len(values)): values.append(values[-1] + values[-2]) return np.array(values) # テストデータに対する誤差を計算する。 def evaluate(loss_calculator, seqs): batches = seqs.shape[0] // BATCH_SIZE clone = loss_calculator.copy() clone.train = False clone.model.reset_state() start = 0 for i in range(batches): seq = seqs[start: start + BATCH_SIZE] start += BATCH_SIZE loss = calculate_loss(clone, seq) return loss if __name__ == '__main__': # _/_/_/ データの作成 dataset = DatasetMaker.make(TOTAL_SIZE, VALUE) if GPU >= 0: dataset = chainer.cuda.to_gpu(dataset) # 訓練データと検証データに分ける。 n_train = int(TOTAL_SIZE * SPRIT_RATE) n_val = TOTAL_SIZE - n_train train_dataset = dataset[: n_train].copy() val_dataset = dataset[n_train:].copy() # 長さSEQUENCE_SIZE + 1の時系列データを始点を1つずつずらして作る。 # +1は教師データ作成のため。 train_seqs = DatasetMaker.make_sequences(train_dataset, SEQUENCE_SIZE + 1) val_seqs = DatasetMaker.make_sequences(val_dataset, SEQUENCE_SIZE + 1) # _/_/_/ モデルの設定 mynet = MyNet(N_LAYERS, N_IN, N_HIDDEN, N_OUT, DROPOUT) if GPU >= 0: mynet.to_gpu() loss_calculator = LossCalculator(mynet) # _/_/_/ 最適化器の作成 optimizer = optimizers.Adam() optimizer.setup(loss_calculator) # _/_/_/ 訓練 batches = train_seqs.shape[0] // BATCH_SIZE print('batches: {}'.format(batches)) losses = [] val_losses = [] for epoch in range(EPOCHS): # エポックの最初でシャッフルする。 xp.random.shuffle(train_seqs) start = 0 for i in range(batches): seq = train_seqs[start: start + BATCH_SIZE] start += BATCH_SIZE # バッチ単位でモデルを更新する。 loss = update_model(loss_calculator, seq) # 検証する。 val_loss = evaluate(loss_calculator, val_seqs) # エポック単位の表示 average_loss = loss.data average_val_loss = val_loss.data print('epoch:{}, loss:{}, val_loss:{}'.format(epoch, average_loss, average_val_loss)) losses.append(average_loss) val_losses.append(average_val_loss) # 保存する。 serializers.save_npz('./chainer_mynet_dropout={}.npz'.format(DROPOUT), mynet) _pickle.dump(losses, open('./chainer_losses_dropout={}.pkl'.format(DROPOUT), 'wb')) _pickle.dump(val_losses, open('./chainer_val_losses_dropout={}.pkl'.format(DROPOUT), 'wb')) |
- CPU/GPUの切り替えを行なっている部分は、17-19行目、140-141行目、157-158行目である。
- 誤差の蓄積は、35行目と56行目のconcat周辺のコードで実現している。concatすることで計算の手間を削減していることに注意する。
予測コード
GPU環境では(EC2上では)予測のあとグラフを描画するために、Jupyterを用いた。コードは、上のセルから順に以下のようになる(nstep_lstm/draw_results.ipynb)。
|
1 2 3 4 5 6 7 8 9 |
from nstep_lstm_using_chainer_with_fibonacci import MyNet, DatasetMaker from chainer import serializers import chainer import numpy as np import matplotlib.pyplot as plt import _pickle from params import * # noqa from predict import * %matplotlib inline |
|
1 |
PLOT_SIZE = 4 * SEQUENCE_SIZE |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# _/_/_/ モデルの読み込み mynet = MyNet(N_LAYERS, N_IN, N_HIDDEN, N_OUT) serializers.load_npz('chainer_mynet_dropout={}.npz'.format(DROPOUT), mynet) # _/_/_/ データの作成 dataset = DatasetMaker.make(TOTAL_SIZE, VALUE) # _/_/_/ 予測 output_seq = predict(mynet, dataset, SEQUENCE_SIZE) # _/_/_/ 視覚化 # 予測した時系列データ plt.figure(figsize=(15, 5)) plt.xlim([0, PLOT_SIZE]) plt.plot(dataset, linestyle='dotted', color='red') plt.plot(output_seq, color='black') plt.show() # 誤差とエポックの間の関係 losses = _pickle.load(open('./chainer_losses_dropout={}.pkl'.format(DROPOUT), 'rb')) val_losses = _pickle.load(open('./chainer_val_losses_dropout={}.pkl'.format(DROPOUT), 'rb')) plt.figure(figsize=(10, 5)) plt.plot(losses, label='loss') plt.plot(val_losses, label='val_loss') plt.ylabel('Loss') plt.xlabel('Epoch') plt.legend() plt.show() |
一番最初のセルでインポートしているモジュールpredictの中身は以下の通りである(nstep_lstm/predict.py)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
#!/usr/bin/env python # -*- coding: utf-8 -*- from nstep_lstm_using_chainer_with_fibonacci import MyNet, DatasetMaker from chainer import serializers import chainer import numpy as np import matplotlib.pyplot as plt import _pickle from params import * # noqa PLOT_SIZE = 4 * SEQUENCE_SIZE xp = np if GPU >= 0: xp = chainer.cuda.cupy def predict_seq(model, input_seq): seq_size = len(input_seq) assert seq_size == SEQUENCE_SIZE for i in range(seq_size): x = chainer.Variable(np.asarray(input_seq[i:i + 1], dtype=np.float32)[:, np.newaxis]) y = model([x]) return y[0].data def predict(model, dataset, seq_size): input_seq = dataset[:seq_size].copy() assert input_seq.shape == (seq_size,) output_seq = np.zeros(seq_size) assert len(dataset) == TOTAL_SIZE model.train = False model.reset_state() for i in range(len(dataset) - seq_size): y = predict_seq(model, input_seq) # 先頭の要素を削除する。 input_seq = np.delete(input_seq, 0) # 末尾にいま予測した値を追加する。 input_seq = np.append(input_seq, y) # 予測値を保存する。 output_seq = np.append(output_seq, y) if i == 4 * SEQUENCE_SIZE: break return output_seq |
予測時のロジックは先の解説を参照のこと。予測時はひとつずつ順に計算していくので、GPUではなくCPU上で計算した。GPU上で計算するとGPUデバイス上へのメモリ転送のオーバヘッドが大きくなるためである。
計算結果
params.py内の定数N_LAYERSだけを変えて計算を行なった。SEQUENCE_SIZE(![]() )とした。予測結果を以下に示す。図の見方は以前と同じである。最初のシーケンスとして正解値を与え、ひとつずつ予測値に置き換えていく。最初のシーケンスは予測値でないので0としてある。
)とした。予測結果を以下に示す。図の見方は以前と同じである。最初のシーケンスとして正解値を与え、ひとつずつ予測値に置き換えていく。最初のシーケンスは予測値でないので0としてある。
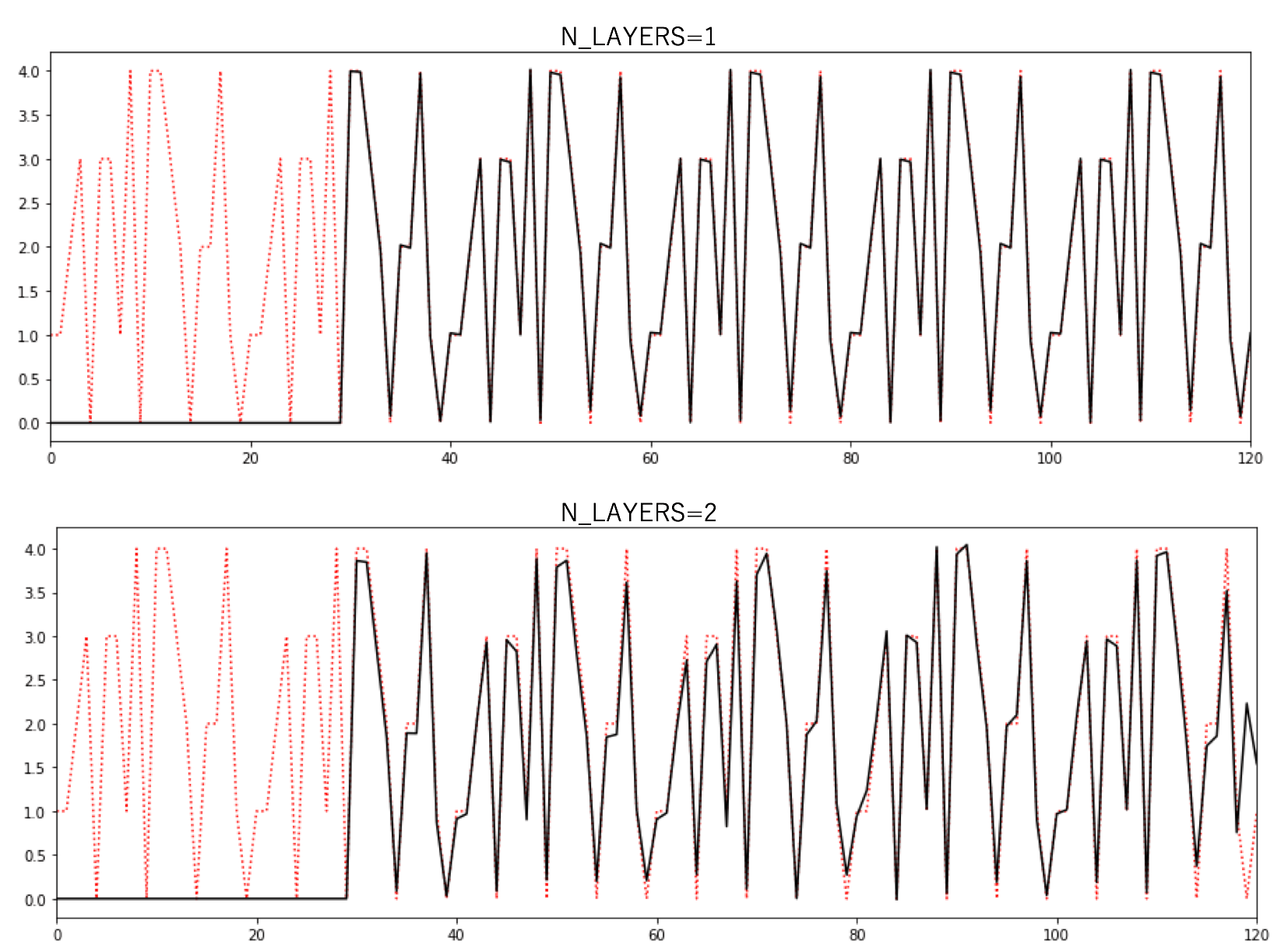
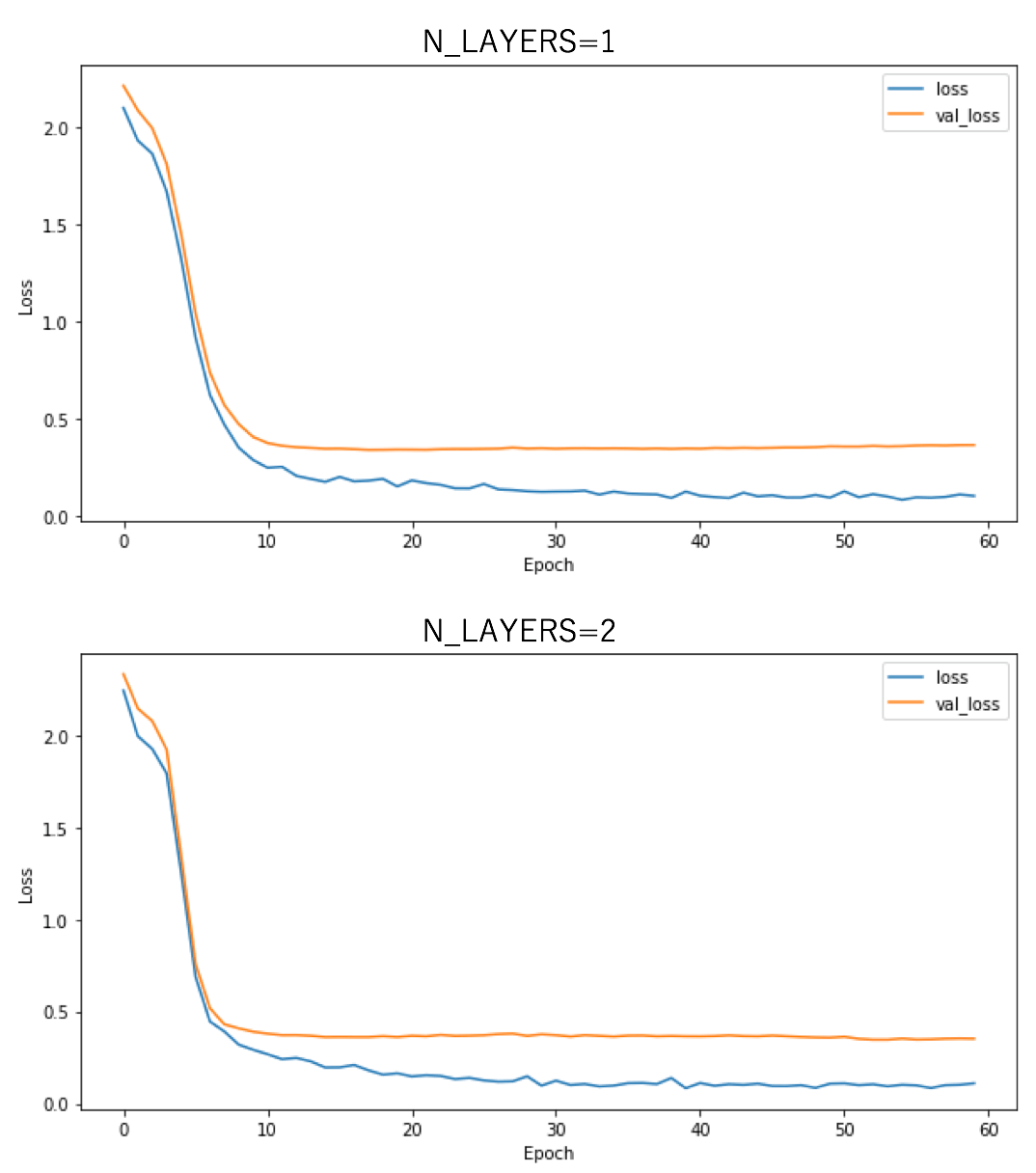
今回の例では、明らかにLSTM層は1層の方が精度が良いことが分かる。多層化が常に精度向上に繋がるわけではないのだろう。以下に示すのは訓練時における損失値のepoch依存性である。
速度比較
CPU/GPU上でLSTMとNStepLSTMの訓練時の速度比較を行なった。NStepLSTMの層数は1、その他のパラメータは上に示したparams.pyと同じである。結果を以下に示す(単位はsec)。3回測定し平均した。ここに掲げていないLSTMのソース(lstm/lstm_using_chainer_with_fibonacci.py)はこちらに置いてある。このスクリプトもGPU版のときはGPU=0、CPU版のときはGPU=-1として使う。
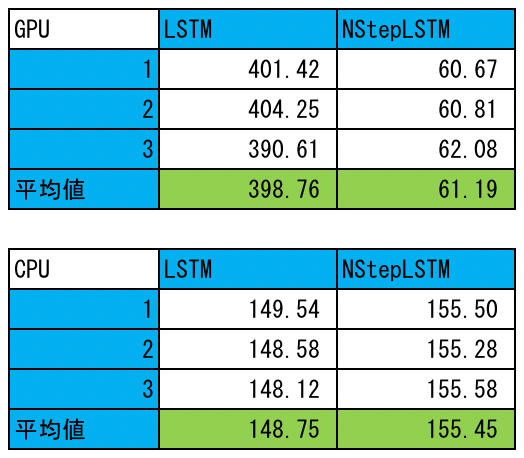
GPU上での結果を見ると、NStepLSTMは確かに高速であることが分かるが(cuDNNのおかげだろう)、LSTMはCPU上のものと比べてもかなり遅いことが分かる。実装の仕方に改良の余地がありそうである(おそらく、__call__に順に渡すxのオーバヘッドが原因だろう)。一方、CPU上での結果を見ると、LSTMとNStepLSTMの間にはそれほど差がないだけでなく、前者の方が速くなっている。
まとめ
今回は、chainer.links.NStepLSTMを用いた実装例を示した。chainer.links.LSTMとはデータの与え方が異なることに注意しなければならない。さらに、GPU上でも動作する仕組みを導入した。GPU上での速度は、NStepLSTMの方が高速であることを確認した。
今回示した例では、多層化による精度向上は見られなかった。しかし、GPU上では高速であること、![]() を可変長にできること、問題によっては多層化が必要になることを考慮すると、NStepLSTMの方を用いるべきであろう。
を可変長にできること、問題によっては多層化が必要になることを考慮すると、NStepLSTMの方を用いるべきであろう。

