PyMCによるMarkov Chain Monte Carlo

はじめに

PythonライブラリPyMCを用いてBayes推論する一連の流れを、以前取り上げた線形回帰を例に解説する。

PyMCとは

最初に、Bayes推論の概要を回帰問題を例に取り説明する。いま、 $X=\{x_1,\cdots,x_N\},Y=\{y_1,\cdots,y_N\}$ が観測されているとする。 $x_i$ が説明変数、 $y_i$ が目的変数である。このとき、潜在変数 $w$ を導入し、同時確率分布 $p(X,Y,w)$ を考える。この分布にBayesの定理を適用すると次式を得る。

(1) $\begin{equation*} p(w|X,Y) = \frac{p(Y|X,w)p(w)}{p(Y|X)} \end{equation*}$

(2) $\begin{equation*} p(y_*|x_*,X,Y)=\int dw\;p(y_*|x_*,w)p(w|X,Y) \end{equation*}$

下図は式(2)を用いて予測を行った具体例である。

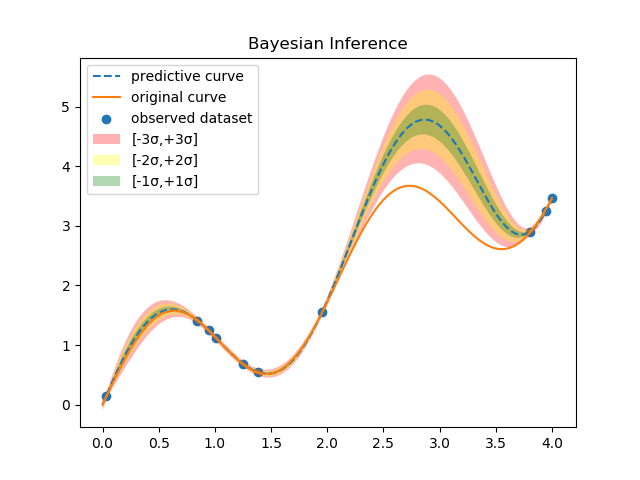
橙色の実線がGround Truthとなる曲線、青丸が適当にサンプルした観測値（10個）、破線が予測曲線である。色ぬりした領域が標準偏差の大きさ、すなわち予測値の不確実さを表す。この図から分かる通り、観測値近傍の標準偏差は小さく、観測値が存在しない領域の標準偏差は大きくなる。Bayes推論の優れた点は、各予測値を点として求めるだけでなく、その確からしさも定量的に導出することができることである。式(2)を計算するためには、事後分布 $p(w|X,Y)$ を求める必要がある。Bayes推論の目的はこの事後分布を解析的あるいは近似的に求めることである。以前取り上げた線形回帰では、事前分布と尤度に正規分布を適用したので、事後分布を解析的に求めることができた（事後分布を同じ関数形にできる事前分布を共役事前分布と呼ぶのであった）。しかし、解析的に計算できるのは非常に限定された関数の組み合わせの場合だけであり、実世界にBayes推論を適用する際には何らかの近似理論を使うのが一般的である。近似理論の１つがMarkov Chain Monte Carlo(MCMC)である。上の例で言えば、計算機を使って事後分布 $p(w|X,Y)$ のサンプル点 $w^{(1)},w^{(2)},\cdots$ を大量に取得し、これらの点の分布から事後分布のおおよその形を知る手法である。一方、事後分布の計算過程に現れる解析計算のできない箇所を、解析計算が可能な関数に置き換える手法や、事後分布を直接求めず、それと良く似た解析的に扱い易い関数 $q_{\phi}(w)$ を導入し、できるだけ真の事後分布に近くなるようにパタメータ $\phi$ を調節する手法もある。今回取り上げるPyMCはMCMCを行うライブラリである。

例題

上で述べたように、PyMCは厳密に計算できない事後確率の場合にその威力を発揮するが、ここでは解析解が既知のものに適用し、どの程度それを再現できるのかを検証してみたい。例題として、以前取り上げた線形回帰を取り上げる。すでに解析解は求められている。同じ問題をPyMCで解き、この解析解と比較する。

PyMCの適用

コードを少しずつ示し、PyMCの構文の説明とそれに対応する理論式を示していく。今回の全コードはここにある。

sample_with_multinormal.py

最初に観測値を読み込む。

    # load a dataset
    dataset = utils.load_dataset(DATASET_PATH)
    observed_xs = dataset[:, 0]
    observed_ys = dataset[:, 1]

# load a dataset

dataset = utils.load_dataset(DATASET_PATH)

observed_xs = dataset[:, 0]

observed_ys = dataset[:, 1]

観測値の様子は以下の通り。

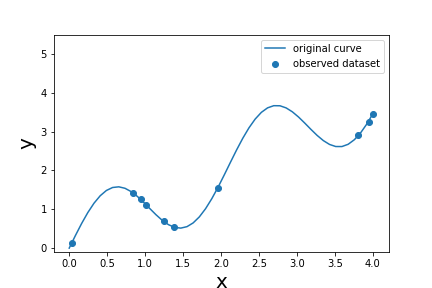
実線は正解曲線を表し、次式で定義される。

(3) $\begin{equation*} y=x+\sin{x} \end{equation*}$

この曲線上の点をランダムに選択したものが観測値である。ただし、平均0、標準偏差0.015のガウスノイズを付加してある。次に事前確率を定義する。

    # define a prior for w, which is a multivariable gaussian
    ws = pymc.MvNormal('ws', mu=np.zeros(M), tau=ALPHA * np.eye(M), value=np.zeros(M))

1 2	# define a prior for w, which is a multivariable gaussian ws = pymc.MvNormal('ws', mu=np.zeros(M), tau=ALPHA * np.eye(M), value=np.zeros(M))

上のコードは次の $M$ 次元正規分布を表す。

(4) $\begin{equation*} p(\vec{w})=\mathcal{N}(\vec{w}|\vec{0},\left(\alpha I\right)^{-1}) \end{equation*}$

クラスpymc.MvNormalのインスタンスwsは一種の乱数生成器であり、PyMCではstochastic変数と呼ばれる。この変数は内部状態をもち、その初期値を引数valueで指定することができる。上のコードでは $\vec{0}$ を渡している。 $M=8$ とした。

    # calculate x^0, x^1, ..., x^{M-1}
    xs = np.empty((M, len(observed_xs)), dtype=np.float32)
    for i in range(M):
        xs[i] = np.power(observed_xs, i)

# calculate x^0, x^1, ..., x^{M-1}

xs = np.empty((M, len(observed_xs)), dtype=np.float32)

for i in range(M):

xs[i] = np.power(observed_xs, i)

上のコードは、 $\vec{x}=(x^0,x^1,\cdots,x^{M-1})$ を計算したものである。

    # define a deterministic function
    linear_regression = pymc.Lambda('linear_regression', lambda xs=xs, ws=ws: ws.dot(xs))

1 2	# define a deterministic function linear_regression = pymc.Lambda('linear_regression', lambda xs=xs, ws=ws: ws.dot(xs))

このコードは以下を計算する関数である。

(5) $\begin{equation*} \vec{w}^{\;T}\vec{x}=w_0 + w_1 x + w_2 x^2 + \cdots + w_{M-1} x^{M-1} \end{equation*}$

この関数の返り値は、入力（引数）の値が同じなら常に同じになる。このような変数を上のstochastic変数と対比させてdeterministic変数と呼ぶ。乱数的な振る舞いはしない変数である。次に尤度を定義する。

    # define a model likelihood
    y = pymc.Normal('y', mu=linear_regression, tau=TAU, value=observed_ys, observed=True)

1 2	# define a model likelihood y = pymc.Normal('y', mu=linear_regression, tau=TAU, value=observed_ys, observed=True)

この式は次式を表す。

(6) $\begin{equation*} p(y|\vec{x},\vec{w})=\mathcal{N}(y|\vec{w}^{\;T}\vec{x},\sigma^2) \end{equation*}$

pymc.Normalのインスタンスyもstochastic変数になる。また、TAU= $1/\sigma^2$ である。観測値のところで示した標準偏差 $\sigma=0.015$ を用いる。今回のBayes推論では、推論すべき量は $\vec{w}$ のみとし、標準偏差については既知の量（ハイパーパラメータ）として扱う。一般的にハイパーパラメータの設定には何らかの事前知識が必要になる。引数valueに観測値observed_ysを渡し、observedをTrueに設定することで、stochastic変数yを観測値に固定する。ここまでの式を用いて以下のようにモデルを作成する。

    # make a model
    model = pymc.Model([y, ws])
    map_ = pymc.MAP(model)
    map_.fit()
    mcmc = pymc.MCMC(model, db='pickle', dbname=PICKLE_PATH)

# make a model

model = pymc.Model([y, ws])

map_ = pymc.MAP(model)

map_.fit()

mcmc = pymc.MCMC(model, db='pickle', dbname=PICKLE_PATH)

2行目でstochastic変数を配列にしてクラスModelのコンストラクタに渡し、そのインスタンスmodelを作成する。3行目と4行目でMAP推定を行う。5行目でMCMCを行うインスタンスmcmcを作る。5行目の前にMAP推定を行うコードを挿入することにより、MAP推定の解を初期値としてサンプリングが実行されることになる。MAP推定のコードはなくても動作するが、あった方が精度は良い。引数dbとdbnameを用いて、モデルを保存するフォーマットとパスを指定する。最後に以下のようにサンプリングを行う。

    # sampling
    mcmc.sample(iter=ITER, burn=BURN, thin=THIN)

1 2	# sampling mcmc.sample(iter=ITER, burn=BURN, thin=THIN)

引数iterにサンプリング総数を指定する。サンプリングの前半部分は精度が悪いため推論には使わない。この前半期間をburn-inと呼び、引数burnで指定する。推論にはサンプリングの後半期間を用いることになる。後半期間のうち、引数thinに指定した回数ごとに値を採用する。今回は、ITER=70000000、BURN=ITER/2=35000000、THIN=3500としたので、結果として得られるサンプル点の個数は10000になる。最後に後始末と結果を保存する。

    mcmc.db.close()

    # save it as csv
    mcmc.write_csv(CSV_PATH, variables=['ws'])

mcmc.db.close()

# save it as csv

mcmc.write_csv(CSV_PATH, variables=['ws'])

4行目で保存されるのは、得られた事後分布の統計値（平均値、標準偏差など）の概要である。ここまでのコードを実行すると、標準出力に以下のような計算過程が表示される。計算時間は46分ほどである（動作環境については後述する）。

[ 0% ] 37783 of 70000000 complete in 1.5 sec
[ 0% ] 50454 of 70000000 complete in 2.0 sec
[ 0% ] 63533 of 70000000 complete in 2.5 sec
…
[– 7% ] 5130706 of 70000000 complete in 207.0 sec
[– 7% ] 5143280 of 70000000 complete in 207.5 sec
[– 7% ] 5156585 of 70000000 complete in 208.0 sec
…
[—————–99%—————– ] 69950855 of 70000000 complete in 2807.1 sec
[—————–99%—————– ] 69963866 of 70000000 complete in 2807.6 sec
[—————–99%—————– ] 69976414 of 70000000 complete in 2808.1 sec
[—————–99%—————– ] 69988507 of 70000000 complete in 2808.6 sec
[—————–100%—————–] 70000000 of 70000000 complete in 2809.1 sec

calculate_predictions_with_multinormal.py

MCMCの計算が終わると、事後確率

(7) $\begin{eqnarray*} p(\vec{w}|X,Y)&=&\mathcal{N}(\vec{w}|\vec{m}_B,\Lambda_B^{-1}) \\ \Lambda_B&=&\sigma^{-2}\sum_{n=1}^N\vec{x}_n\vec{x}_n^T+\alpha I \\ \vec{m}_B&=&\sigma^{-2}\Lambda_B^{-1}\sum_{n=1}^{N}y_n\vec{x}_n \end{eqnarray*}$

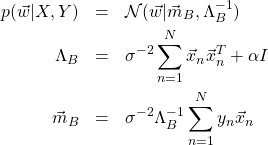
の近似解（サンプル点）が得られる。これを用いて予測曲線を計算する過程を次に示す。
最初に、先に保存したインスタンスmcmcを読み込む。

    # load a model
    mcmc = pymc.database.pickle.load(PICKLE_PATH)

1 2	# load a model mcmc = pymc.database.pickle.load(PICKLE_PATH)

次に、事後確率のサンプル点を取り出す。

    # extract samples for posteriors
    ws = mcmc.trace('ws')[:]

1 2	# extract samples for posteriors ws = mcmc.trace('ws')[:]

wsはnumpyの行列であり、そのshapeは(8,10000)である。すなわち、１つの変数 $w_i$ につき10000個の点がサンプリングされている。予測曲線を描くため $x$ の値域を定義し、 $(x^0,x^1,\cdots,x^{M-1})$ を計算する。

    # calculate x^0,x^1,...,x^{M-1}
    ixs = np.linspace(XMIN, XMAX, XCOUNT)
    xs = np.empty((M, XCOUNT))
    for i in range(M):
        xs[i, :] = np.power(ixs, i)

# calculate x^0,x^1,...,x^{M-1}

ixs = np.linspace(XMIN, XMAX, XCOUNT)

xs = np.empty((M, XCOUNT))

for i in range(M):

xs[i, :] = np.power(ixs, i)

ここで、XMIN=0、XMAX=4、XCOUNT=50である。次に関数

def linear_regression(xs, ws):
    return ws.dot(xs)

1 2	def linear_regression(xs, ws): return ws.dot(xs)

を定義し、以下のように $\vec{w}^T\vec{x}$ を計算する。

    # calculate ys
    ys = linear_regression(xs, ws)

1 2	# calculate ys ys = linear_regression(xs, ws)

ysのshapeは(10000,50)である。50はXOUNTに相当する。次に、10000個の平均値と標準偏差を計算する。

    # calculate statistics
    ymeans = ys.mean(axis=0)
    ystds = ys.std(axis=0)

# calculate statistics

ymeans = ys.mean(axis=0)

ystds = ys.std(axis=0)

ymeansとystdsのshapeは(50,)である。前者が予測曲線の平均値、後者が予測曲線の標準偏差に相当する。最後にこれらを保存する。

    # save them
    np.save(YMEANS_PATH, ymeans)
    np.save(YPREDICTIONS_PATH, ys)
    np.save(YSTDS_PATH, ystds)
    np.save(IXS_PATH, ixs)

# save them

np.save(YMEANS_PATH, ymeans)

np.save(YPREDICTIONS_PATH, ys)

np.save(YSTDS_PATH, ystds)

np.save(IXS_PATH, ixs)

visualize_predictions.py

保存した結果を読み込み描画する。コードの説明は省略し、グラフだけを示す。最初のグラフは、解析解と比較したものである。

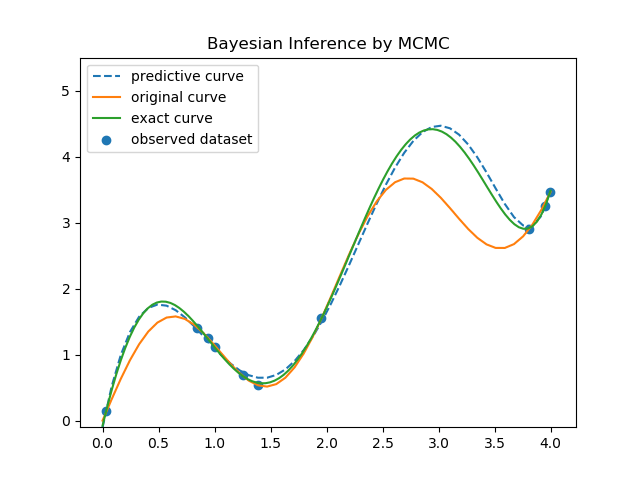
凡例の意味は以下の通り。

predictive curve: MCMCによる予測曲線

original curve: 観測点をサンプリングした元の曲線

exact curve: 解析解による予測曲線

observed dataset: 観測点

解析解と良く一致していることがわかる。次に、標準偏差まで含めたグラフを示す。

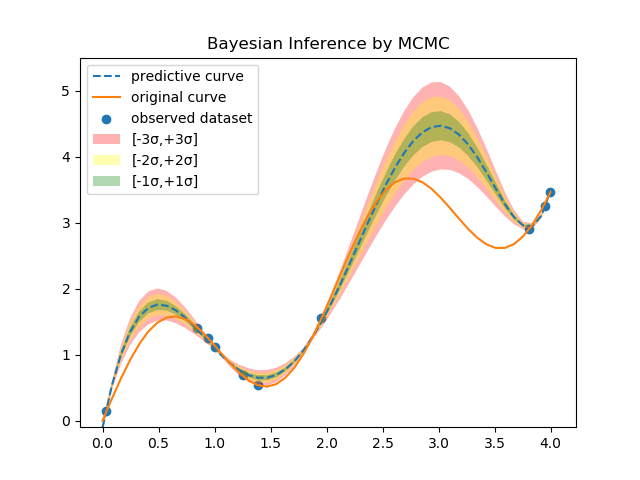
一方、解析解の結果は以下の通りである。

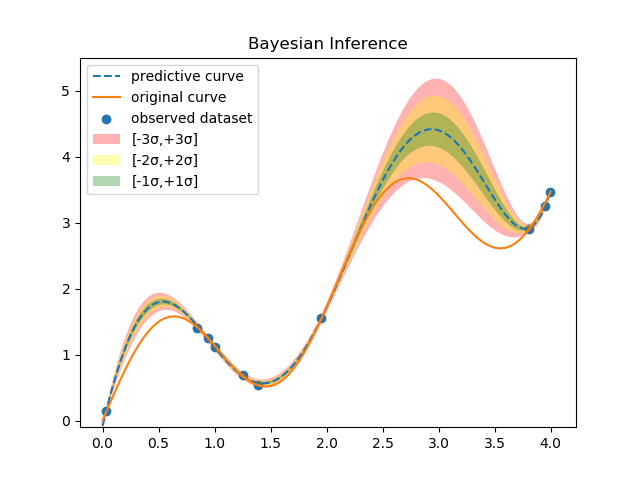
おおよその振る舞いは再現できていることが分かる。

開発環境

動作確認した環境は以下の通りである。

MacBook Pro(15-inch, Late 2016)

プロセッサ：2.9 GHz Intel Core i7

メモリ：16 GB 2133 MHz LPDDR3

Python環境：Python 3.6.2(Anaconda custom)

PyMC：2.3.6

まとめ

今回は、Markov Chain Monte Carlo(MCMC)を用いたBayes推論を、ライブラリPyMCを用いて行った。先に説明したように事後分布を解析的に計算することは一般的に困難である。このような場合の近似理論の１つがMCMCであり、PyMCはMCMCを手軽に行うことができるライブラリである。「手軽」と書いたが、ある程度の慣れは必要である。サンプリング回数、burn-inする期間、事前確率の初期値の設定などは試行錯誤が必要である。また、今回のように多次元の線形回帰を行う場合は、かなりの数のサンプリングが必要になる。今回の例では、70000000（7千万）点で解析解に近い答えが得られた。計算時間は46分ほどである。しかしながら、解析的に扱えない事後確率を得る強力なツールには違いない。
PyMCを触り始めてまだ日が浅い。今回の結果を得るまでにかなりの時間を費やした。1次元正規分布の場合のPyMCのサンプルコードはいくらでも見つかるが、多次元の場合の例を見つけることができなかった。なので、全コードがオリジナルである。よりエレガントな書き方があれば指摘してほしい。

参考文献

Pythonで体験するベイズ推論
本書はPyMCの入門書である。ただし、PyMCのバージョンは2である。今回示した例もPyMC2である。最近ではPyMC3が多く使われている。

Kumada Seiya

仕事であろうとなかろうと勉強し続ける、その結果”中身”を知ったエンジニアになれる

エンジニアに文系・理系は関係ない

【C#】DataGridViewデータ表示速度比較

PyMCによるMarkov Chain Monte Carlo

はじめに

PyMCとは

例題

PyMCの適用

sample_with_multinormal.py

calculate_predictions_with_multinormal.py

visualize_predictions.py

開発環境

まとめ

参考文献

Kumada Seiya

最近の記事

顔認証（DeepFace vs GPT4o）

時系列解析再訪

πの新しい公式

中心極限定理

DBSCANを用いたクラスタリング

レイアウト解析

Amazon SageMakerのAPIを使った賢いWebアプリの作り方

ポアソン分布とは何なのか、とにかく全力で分かりやすく解説する

行列の条件数

時系列解析-4

最小二乗法とその周辺

Tesseract OCR

Google Vision APIでOCR

アーカイブ

カテゴリー