囲み枠c
はじめに
今回は、ChainerによるLSTMの実装例を示し、Fibonacci数列から作られる周期関数に適用した結果を示す。
LSTM(Long Short Term Memory)
LSTMは、時系列データ![]() が与えられた時、その並びの中に存在する規則性を見い出し、
が与えられた時、その並びの中に存在する規則性を見い出し、![]() を予測するネットワークである。LSTMの構造を以下に示す。
を予測するネットワークである。LSTMの構造を以下に示す。
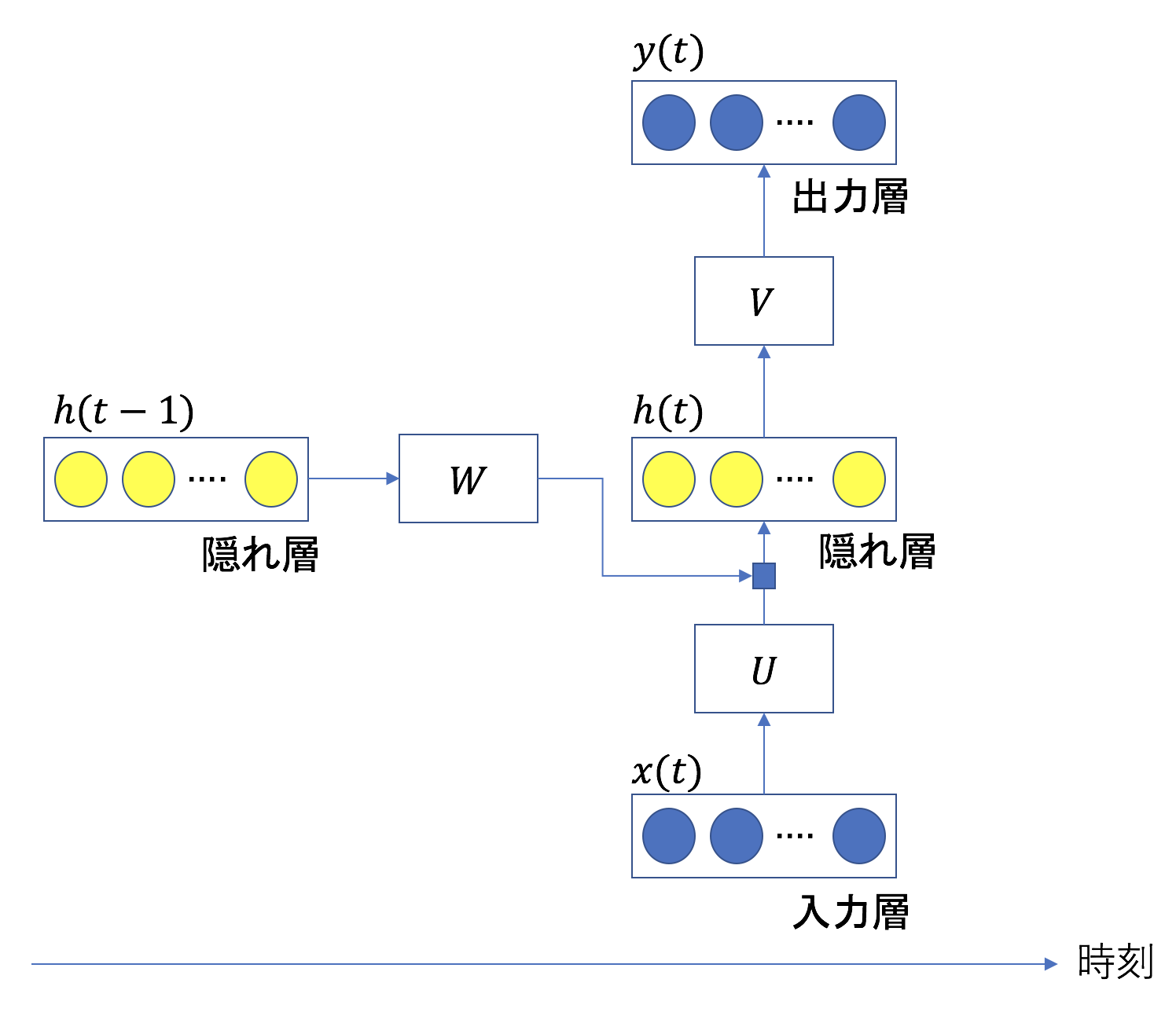
ここで、![]() は、それぞれ時刻
は、それぞれ時刻![]() における入力値、隠れ層の値、出力値である。
における入力値、隠れ層の値、出力値である。![]() は、これらのベクトルに乗算される行列である。現在の入力値と直前の時刻での隠れ層の値が足し合わされ、現在の隠れ層の値になる。
は、これらのベクトルに乗算される行列である。現在の入力値と直前の時刻での隠れ層の値が足し合わされ、現在の隠れ層の値になる。
(1) ![]()
ここで、![]() は活性化関数である。上式からわかる通り、隠れ層は過去のデータを現在のデータに反映させるための層である。隠れ層の各ユニット(黄色い丸)はLSTMブロックと呼ばれ、以下4つの構造をその内部に持つ(黄色い丸を入出力と同じユニットに置き換えると通常のRNNになる)。
は活性化関数である。上式からわかる通り、隠れ層は過去のデータを現在のデータに反映させるための層である。隠れ層の各ユニット(黄色い丸)はLSTMブロックと呼ばれ、以下4つの構造をその内部に持つ(黄色い丸を入出力と同じユニットに置き換えると通常のRNNになる)。
- CEC(Constant Error Carousel)
- 入力ゲート
- 出力ゲート
- 忘却ゲート
CECは、長周期データを扱う際に問題となる勾配消失を抑制するために追加されたユニットである。入力・出力ゲートは、過去の値が必要なときは開き、そうでない場合は閉じる仕組みである。これを導入することにより、長周期の規則性を検出することが可能となる。しかし、入力・出力ゲートは、過去のデータをLSTMブロック内に留めておく機構であるため、時系列データが急激に変化するような場合、その変化に対応できない。これに対処するのが忘却ゲートである。忘却ゲートは、内部に記憶しておく必要がなくなった情報を忘れるための仕組みである。
![]() から
から![]() を予測する様子を示すため、上の図を時間方向にさらに接続したものを次に示す。
を予測する様子を示すため、上の図を時間方向にさらに接続したものを次に示す。
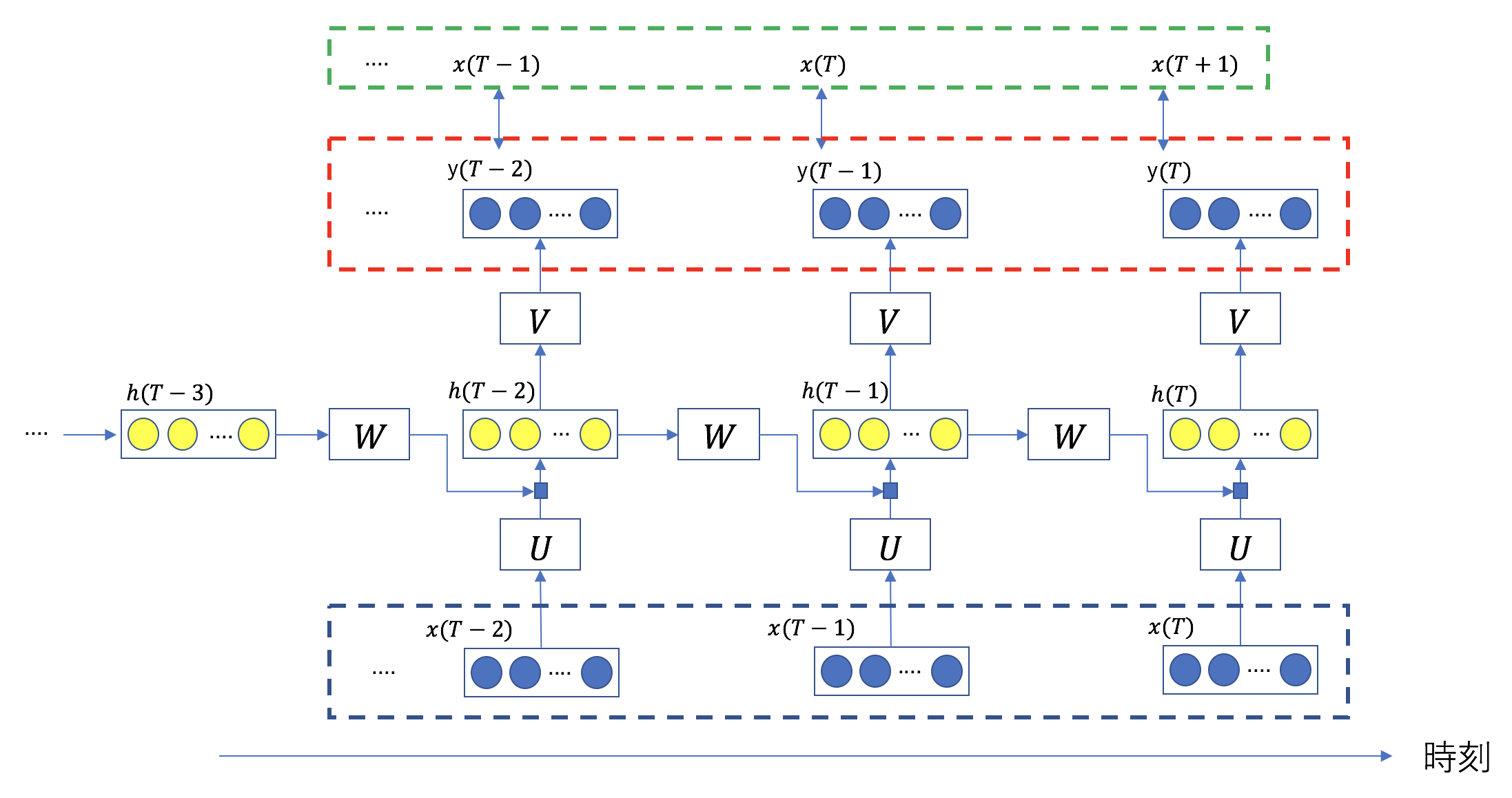
図中の青い矩形で囲んだデータが入力値、赤い矩形で囲んだ値が出力値である。赤い矩形と緑の矩形の間の2乗誤差の和
(2) 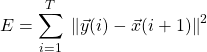
が最小となるようにネットワークを訓練する。
教師データの構成
教師データの作成手順は以下の通りである。
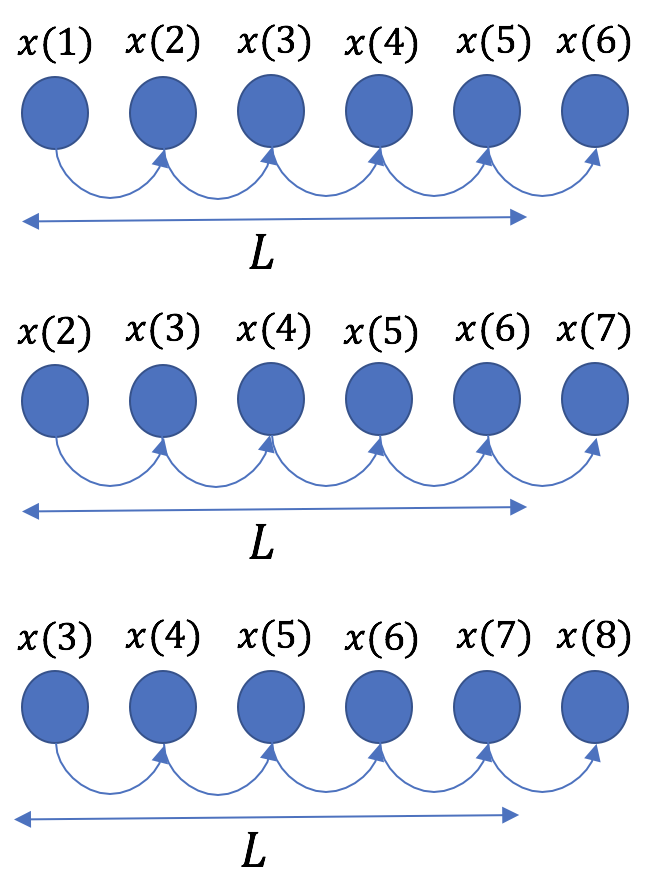
- 十分に長い時系列データを用意する。
- 始点を1つずつずらながら、適当な長さ
 で時系列データを分割する(下図参照)。
で時系列データを分割する(下図参照)。 - 長さ
 内の各値は直後の値を予測するための入力値となる(下図参照)。
内の各値は直後の値を予測するための入力値となる(下図参照)。

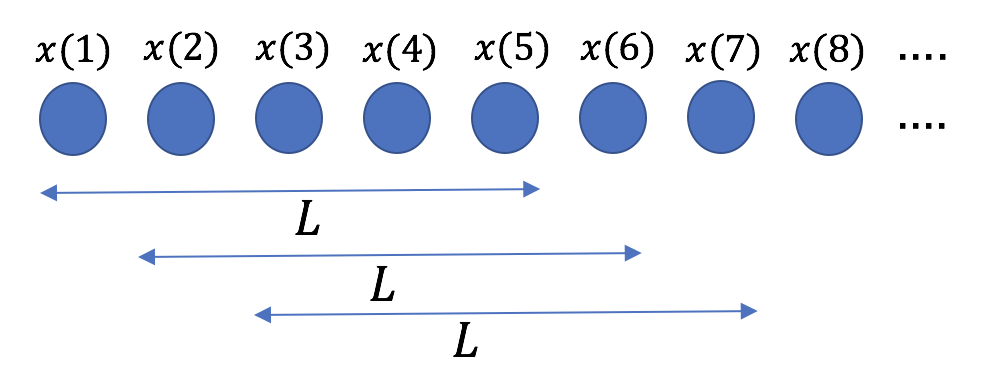
長さ![]() のシーケンス内で2乗誤差の和を計算し、これを最小にする。この手順を切り出したシーケンスの数だけ繰り返す。
のシーケンス内で2乗誤差の和を計算し、これを最小にする。この手順を切り出したシーケンスの数だけ繰り返す。
周期関数の生成
Fibonacci数列は次の漸化式を満たす数列である。
(3) ![]()
この数列を任意の自然数で割った余りは、次の表に示すような周期を持つ。

5で割った時の数字の並びは以下のようになる。
(4) ![]()
太字で示した部分が1つの周期である。今回はこの周期20の数列をLSTMで学習する。
動作環境
- macOS Sierra
- Python 3.6.2
- Chainer 3.0.0
Chainerによる実装例(訓練)
ここまでのロジックを実装したものが以下である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import chainer from chainer import optimizers import chainer.links as L import chainer.functions as F import numpy as np from chainer import serializers import _pickle # fibonacci数列を割る値 VALUE = 5 # 常に同じ計算をする。 np.random.seed(0) # 時系列データの全長 TOTAL_SIZE = 2000 # 訓練とテストの分割比 SPRIT_RATE = 0.9 # 入力時の時系列データ長 SEQUENCE_SIZE = 50 EPOCHS = 30 BATCH_SIZE = 100 # 入力層の次元 N_IN = 1 # 隠れ層の次元 N_HIDDEN = 200 # 出力層の次元 N_OUT = 1 # LSTM class MyNet(chainer.Chain): def __init__(self, n_in=1, n_hidden=20, n_out=1, train=True): super(MyNet, self).__init__() with self.init_scope(): self.l1 = L.LSTM(n_in, n_hidden, lateral_init=chainer.initializers.Normal(scale=0.01)) self.l2 = L.Linear(n_hidden, n_out, initialW=chainer.initializers.Normal(scale=0.01)) self.train = train def __call__(self, x): with chainer.using_config('train', self.train): h = self.l1(x) y = self.l2(h) return y def reset_state(self): self.l1.reset_state() # 損失値計算器 class LossCalculator(chainer.Chain): def __init__(self, model): super(LossCalculator, self).__init__() with self.init_scope(): self.model = model def __call__(self, x, t): y = self.model(x) loss = F.mean_squared_error(y, t) return loss # バッチ単位で1つのシーケンスを学習する。 def calculate_loss(model, seq): rows, cols = seq.shape assert cols - 1 == SEQUENCE_SIZE loss = 0 # 1つのシーケンスを全て計算する。 for i in range(cols - 1): # batch単位で計算する。 x = chainer.Variable( np.asarray( [seq[j, i + 0] for j in range(rows)], dtype=np.float32 )[:, np.newaxis] ) t = chainer.Variable( np.asarray( [seq[j, i + 1] for j in range(rows)], dtype=np.float32 )[:, np.newaxis] ) # 誤差を蓄積する。 loss += model(x, t) return loss # モデルを更新する。 def update_model(model, seq): loss = calculate_loss(model, seq) # 誤差逆伝播 loss_calculator.cleargrads() loss.backward() # バッチ単位で古い記憶を削除し、計算コストを削減する。 loss.unchain_backward() # バッチ単位で更新する。 optimizer.update() return loss # Fibonacci数列から周期関数を作る。 class DatasetMaker(object): @staticmethod def make(total_size, value): return (DatasetMaker.fibonacci(total_size) % value).astype(np.float32) # 全データを入力時のシーケンスに分割する。 @staticmethod def make_sequences(data, seq_size): data_size = len(data) row = data_size - seq_size seqs = np.ndarray((row, seq_size)).astype(np.float32) for i in range(row): seqs[i, :] = data[i: i + seq_size] return seqs @staticmethod def fibonacci(size): values = [1, 1] for _ in range(size - len(values)): values.append(values[-1] + values[-2]) return np.array(values) # テストデータに対する誤差を計算する。 def evaluate(loss_calculator, seqs): batches = seqs.shape[0] // BATCH_SIZE clone = loss_calculator.copy() clone.train = False clone.model.reset_state() start = 0 for i in range(batches): seq = seqs[start: start + BATCH_SIZE] start += BATCH_SIZE loss = calculate_loss(clone, seq) return loss if __name__ == '__main__': # _/_/_/ データの作成 dataset = DatasetMaker.make(TOTAL_SIZE, VALUE) # 訓練データと検証データに分ける。 n_train = int(TOTAL_SIZE * SPRIT_RATE) n_val = TOTAL_SIZE - n_train train_dataset = dataset[: n_train].copy() val_dataset = dataset[n_train:].copy() # 長さSEQUENCE_SIZE + 1の時系列データを始点を1つずつずらして作る。 # +1は教師データ作成のため。 train_seqs = DatasetMaker.make_sequences(train_dataset, SEQUENCE_SIZE + 1) val_seqs = DatasetMaker.make_sequences(val_dataset, SEQUENCE_SIZE + 1) # _/_/_/ モデルの設定 mynet = MyNet(N_IN, N_HIDDEN, N_OUT) loss_calculator = LossCalculator(mynet) # _/_/_/ 最適化器の作成 optimizer = optimizers.Adam() optimizer.setup(loss_calculator) # _/_/_/ 訓練 batches = train_seqs.shape[0] // BATCH_SIZE print('batches: {}'.format(batches)) losses = [] val_losses = [] for epoch in range(EPOCHS): # エポックの最初でシャッフルする。 np.random.shuffle(train_seqs) start = 0 for i in range(batches): seq = train_seqs[start: start + BATCH_SIZE] start += BATCH_SIZE # バッチ単位でモデルを更新する。 loss = update_model(loss_calculator, seq) # 検証する。 val_loss = evaluate(loss_calculator, val_seqs) # エポック単位の表示 average_loss = loss.data / SEQUENCE_SIZE average_val_loss = val_loss.data / SEQUENCE_SIZE print('epoch:{}, loss:{}, val_loss:{}'.format(epoch, average_loss, average_val_loss)) losses.append(average_loss) val_losses.append(average_val_loss) # 保存する。 serializers.save_npz('./chainer_mynet.npz', mynet) _pickle.dump(losses, open('./chainer_losses.pkl', 'wb')) _pickle.dump(val_losses, open('./chainer_val_losses.pkl', 'wb')) |
実行時のエポック数と誤差値の関係は以下の通りである。
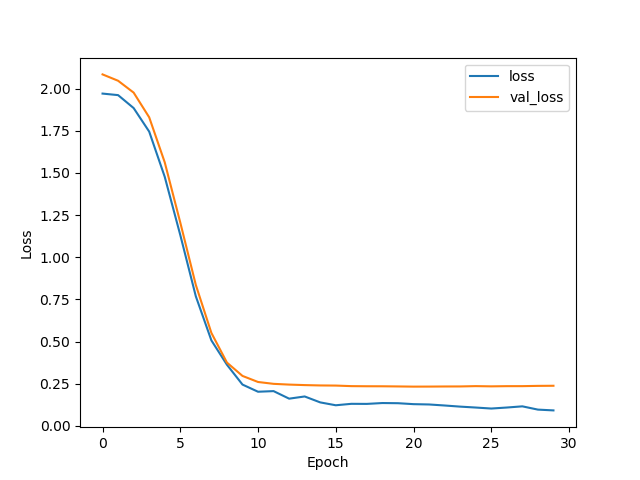
ここで、lossは訓練データに対する誤差(上の式(2)に相当するもの)、val_lossはテストデータに対する誤差を表す。
Chainerによる実装例(予測)
実装例を示す前に、予測時のデータの与え方を以下に示す(下図参照)。
- 訓練時の時系列データを用意する。
- 訓練時と同じ長さ
 で最初のシーケンスを取り出す。
で最初のシーケンスを取り出す。 - このシーケンスを用いて、
 個目の値を予測する。
個目の値を予測する。 - シーケンスの初項を切り捨て、末尾に、いま予測した値を追加する。新たな長さ
 のシーケンスが出来上がる。
のシーケンスが出来上がる。 - 同じことを繰り返す。
- シーケンスに占める予測値の割合が増えていき、
 ステップ目で全ての値が予測値に置き換わる。
ステップ目で全ての値が予測値に置き換わる。
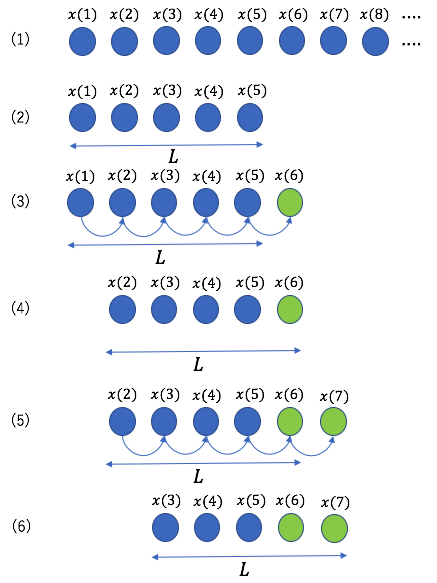
予測時に使用するプログラムは以下の通りである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
#!/usr/bin/env python # -*- coding: utf-8 -*- from lstm_using_chainer_with_fibonacci import MyNet, DatasetMaker from chainer import serializers import chainer import numpy as np import matplotlib.pyplot as plt import _pickle VALUE = 5 N_IN = 1 N_HIDDEN = 200 N_OUT = 1 TOTAL_SIZE = 2000 SEQUENCE_SIZE = 50 PLOT_SIZE = 4 * SEQUENCE_SIZE def predict_seq(model, input_seq): seq_size = len(input_seq) assert seq_size == SEQUENCE_SIZE for i in range(seq_size): x = chainer.Variable(np.asarray(input_seq[i:i + 1], dtype=np.float32)[:, np.newaxis]) y = model(x) return y.data def predict(model, dataset, seq_size): input_seq = dataset[:seq_size].copy() assert input_seq.shape == (seq_size,) output_seq = np.zeros(seq_size) assert len(dataset) == TOTAL_SIZE model.train = False model.reset_state() for i in range(len(dataset) - seq_size): y = predict_seq(model, input_seq) # 先頭の要素を削除する。 input_seq = np.delete(input_seq, 0) # 末尾にいま予測した値を追加する。 input_seq = np.append(input_seq, y) # 予測値を保存する。 output_seq = np.append(output_seq, y) return output_seq if __name__ == '__main__': # _/_/_/ モデルの読み込み mynet = MyNet(N_IN, N_HIDDEN, N_OUT) serializers.load_npz('chainer_mynet.npz', mynet) # _/_/_/ データの作成 dataset = DatasetMaker.make(TOTAL_SIZE, VALUE) # _/_/_/ 予測 output_seq = predict(mynet, dataset, SEQUENCE_SIZE) # _/_/_/ 視覚化 # 予測した時系列データ plt.figure(figsize=(10, 5)) plt.xlim([0, PLOT_SIZE]) plt.plot(dataset, linestyle='dotted', color='red') plt.plot(output_seq, color='black') plt.show() # 誤差とエポックの間の関係 losses = _pickle.load(open('./chainer_losses.pkl', 'rb')) val_losses = _pickle.load(open('./chainer_val_losses.pkl', 'rb')) plt.plot(losses, label='loss') plt.plot(val_losses, label='val_loss') plt.ylabel('Loss') plt.xlabel('Epoch') plt.legend() plt.show() |
![]() の長さを色々変えて予測した結果を以下に示す。
の長さを色々変えて予測した結果を以下に示す。![]() 以外のパラメータは同じである。
以外のパラメータは同じである。
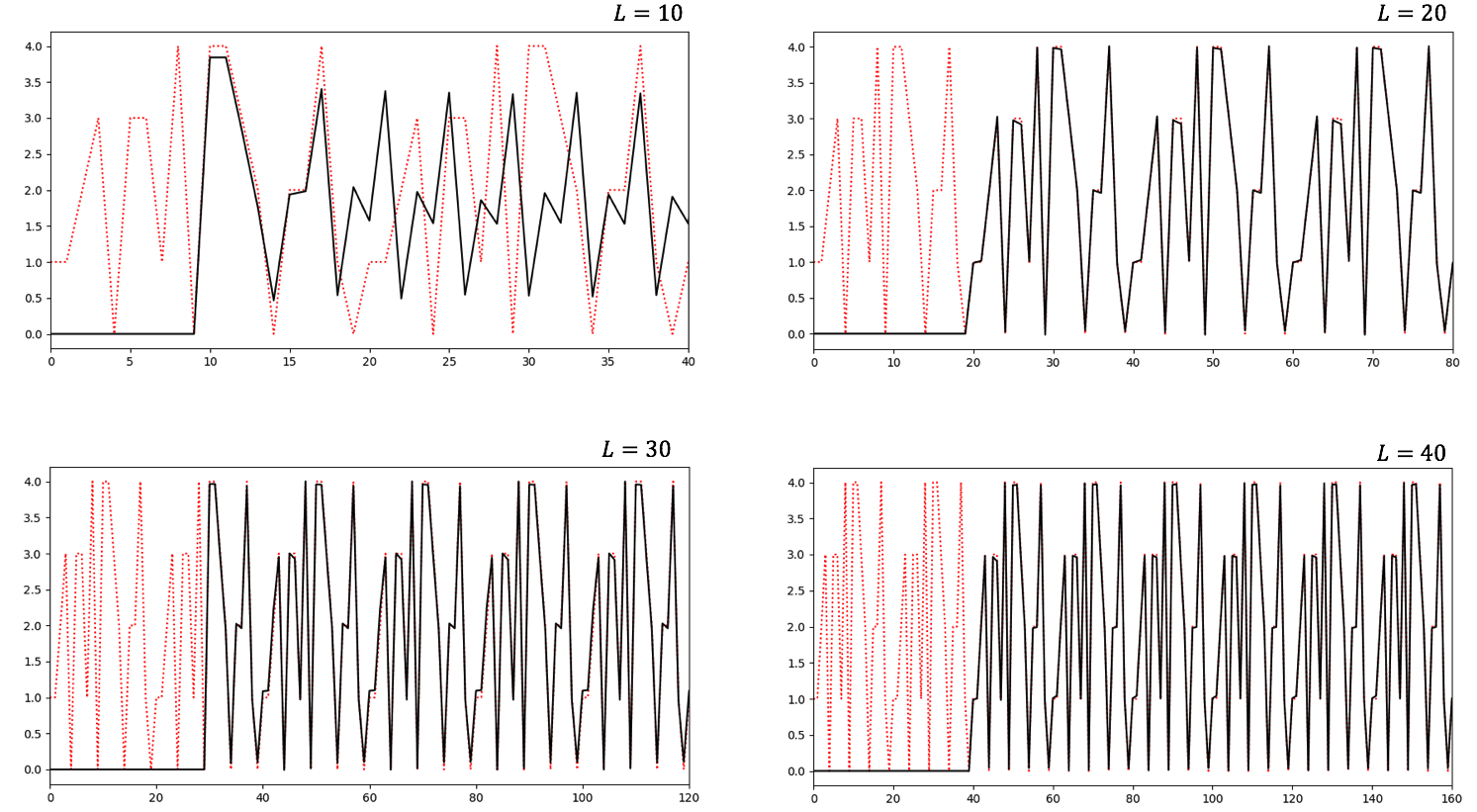
黒線が予測値、赤い点線が正解値である。横軸の長さは![]() とした。横軸最初の
とした。横軸最初の![]() ステップは、予測値ではないので0としてある。
ステップは、予測値ではないので0としてある。![]() で波形をほぼ予測できていることが分かる。元の関数が周期20を持つことから、
で波形をほぼ予測できていることが分かる。元の関数が周期20を持つことから、![]() として少なくとも1周期分必要であるということである。
として少なくとも1周期分必要であるということである。
まとめ
今回は、ChainerによるLSTMの実装を行った。ネットを検索するとChainerを用いたLSTMの実装例はたくさん見つかるが、疑問の余地なく理解できるサンプルは少ないのではないか。Chainerのソースに含まれるサンプルを読み解きながら、自分なりに納得できる形に仕上げたものが今回の実装例である。chainer.training.Trainerは敢えて使用していない。ロジックの流れがわかり難くなるためである。
今回の実装では、chainer.initializersが結果に与える影響が大変大きかった。chainer.initializers.Normalで安定した結果が得られるようになった。
補足
今回取り上げた例では時系列データのパラメータを時刻としているが、時刻である必要はない。値の並びに意味があるデータは全て時系列データである。
KerasとTensorflowによるLSTMの実装が、例えば「詳解ディープラーニング TensorFlow・Kerasによる時系列データ処理」(著者:巣籠悠輔)にも記載されている。純粋にコード量で比較すると、Tensorflow > Chainer > Kerasとなる(この本は良書です)。