はじめに
分類問題に適用される機械学習の手法は、以下の3つに大別できる(下図参照)。
- 識別関数を用いるもの
- 識別モデルを用いるもの
- 生成モデルを用いるもの
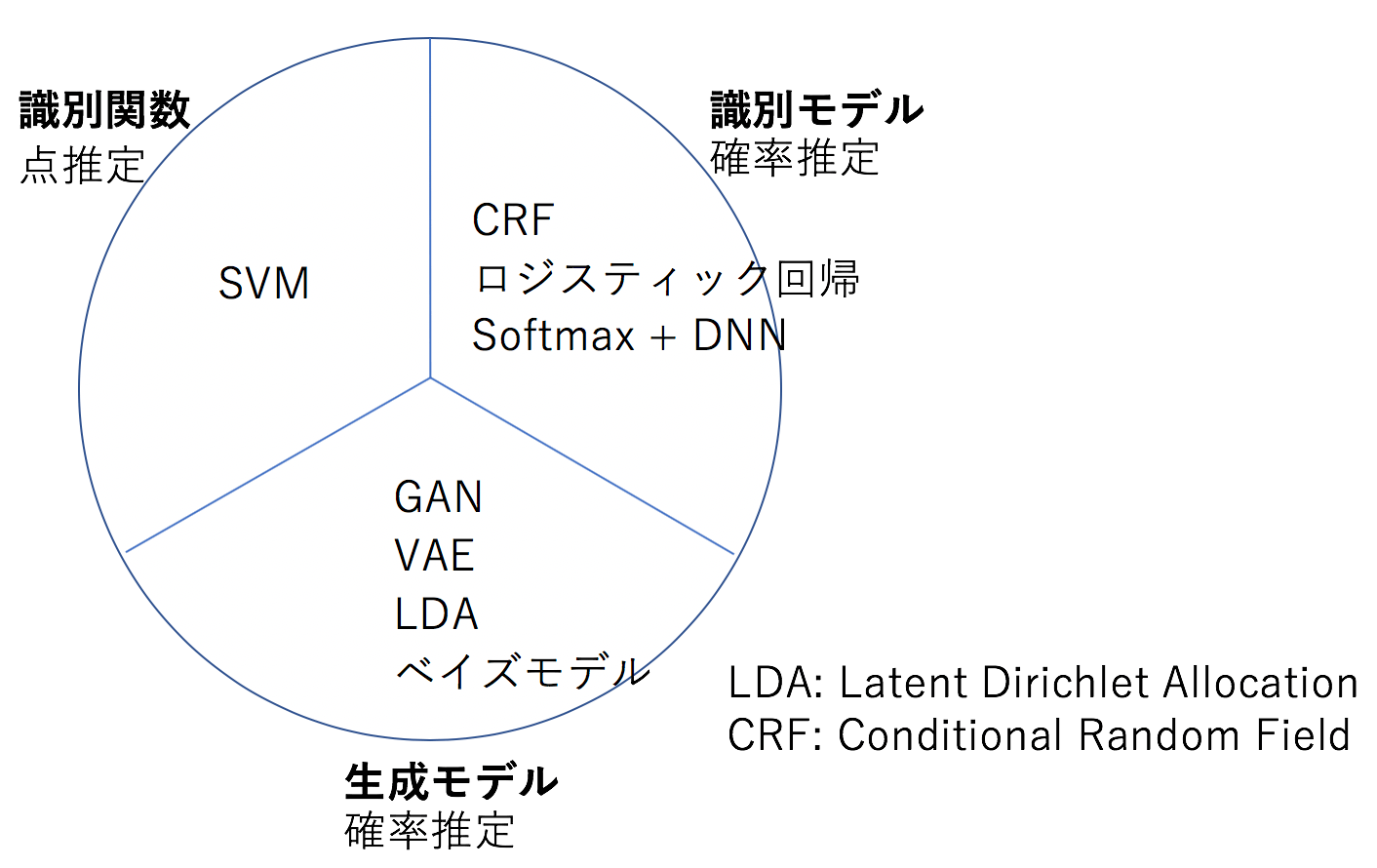
識別関数は1つの点を推定するが、識別モデルと生成モデルは確率を推定する。各手法の代表的なアルゴリズムも上図に示した。
今回の記事では、2分類問題を取り上げ、識別モデルと生成モデルの2つのアプローチでこれを解き、それぞれの手法の特長を解説する。
ソースコード
今回のソースコードはここにあるsample.ipynbである。
識別モデル
いま、観測データ![]() が与えられているとする。ここで
が与えられているとする。ここで
(1) ![]()
である。パラメータ![]() を導入し、同時確率分布
を導入し、同時確率分布![]() を考える。ベイズの定理から次式を得る。
を考える。ベイズの定理から次式を得る。
(2) ![]()
最初に尤度![]() をBernoulli分布を用いてモデル化する。
をBernoulli分布を用いてモデル化する。
(3) 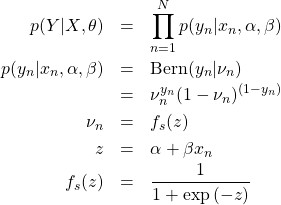
次に事前分布![]() をモデル化する。
をモデル化する。
(4) 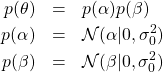
ここで、![]() は平均
は平均![]() 、標準偏差
、標準偏差![]() の正規分布を表す。先に与えた関数
の正規分布を表す。先に与えた関数![]() はシグモイド関数である(下図参照)。
はシグモイド関数である(下図参照)。
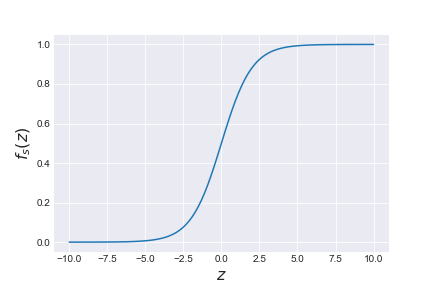
この関数の値は![]() が1になる確率に相当するので、0と1を分離する境界線は
が1になる確率に相当するので、0と1を分離する境界線は![]() となる
となる![]() の値、
の値、![]() から求めることができる。すなわち
から求めることができる。すなわち
(5) ![]()
故に
(6) ![]()
が境界線となる。以上の準備のあと事後確率、![]() と
と![]() を求めることになる。
を求めることになる。![]() はあらかじめ与える定数である。
はあらかじめ与える定数である。
先に見た尤度![]() は、
は、![]() を与えて、それが属するクラス
を与えて、それが属するクラス![]() を識別するモデルとなっている。これが識別モデルと呼ばれる所以である。
を識別するモデルとなっている。これが識別モデルと呼ばれる所以である。
生成モデル
同時確率分布![]() に戻る。この分布はベイズの定理より以下のように変形することもできる。
に戻る。この分布はベイズの定理より以下のように変形することもできる。
(7) ![]()
最初に尤度![]() をモデル化する。
をモデル化する。
(8) 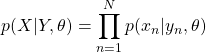
ここで、![]() が0のときの分布と1のときの分布に分けて考える。
が0のときの分布と1のときの分布に分けて考える。
(9) ![]()
どちらも正規分布とする。その標準偏差は共通の値とし、平均だけを異なるものとする。次に、事前分布![]() をモデル化する。
をモデル化する。
(10) 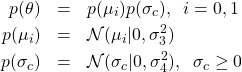
![]() はあらかじめ与える定数である。2つの
はあらかじめ与える定数である。2つの![]() の分布を正規分布とし、その標準偏差を同じものとしたので、2つの分布の境界線は次式で与えられる。
の分布を正規分布とし、その標準偏差を同じものとしたので、2つの分布の境界線は次式で与えられる。
(11) ![]()
以上の準備のあと事後確率、![]() 、
、![]() 、
、![]() を求めることになる。
を求めることになる。
ここでは尤度として2つの![]() の分布を考えた。すなわち、各クラス
の分布を考えた。すなわち、各クラス![]() に属するサンプル
に属するサンプル![]() を生成するモデルとなっている。これが生成モデルと呼ばれる所以である。
を生成するモデルとなっている。これが生成モデルと呼ばれる所以である。
PyMC3による実装
ここまでの計算を、データセット「iris」を用いてPyMC3により行う。このデータセットにはアヤメの3品種
- setosa
- versicolor
- virgnica
が50個ずつ集められており、4つの特徴量
- がく片の長さ:sepal length
- がく片の幅:sepal width
- 花びらの長さ:petal length
- 花びらの幅:petal width
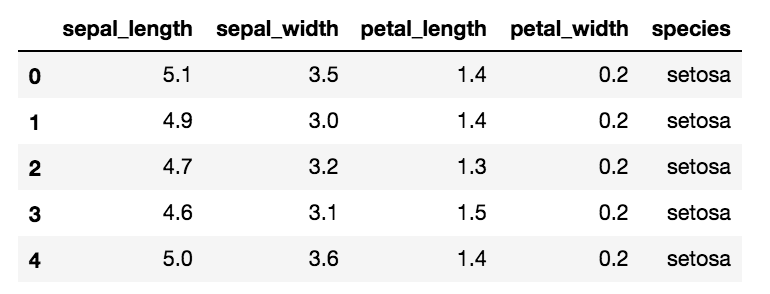
の値が格納されている。データの先頭の様子は以下の通りである。
sepal_lengthについてのバイオリン図を次に示す。縦軸はsepal_lengthの値、横軸は3つの品種を表す。
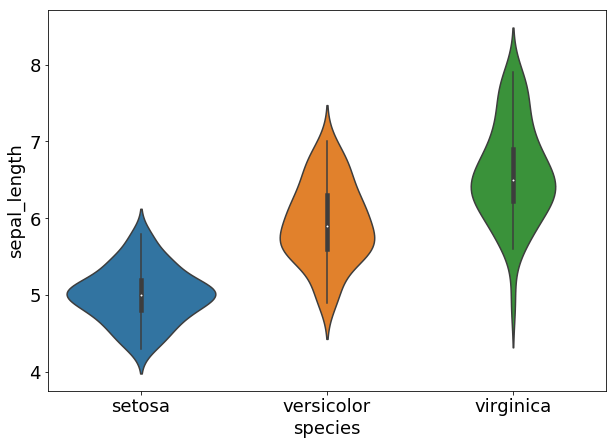
バイオリン図とは、ヒストグラムを縦軸に沿って描画し、それを左右に展開したものである。今回は4つの特徴量の中のsepal lengthを![]() 、setosaとversicolorの2品種を
、setosaとversicolorの2品種を![]() として用いる。
として用いる。
最初に識別モデルを考える。コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 |
import pymc3 as pm with pm.Model() as model_0: alpha = pm.Normal('alpha', mu=0, sd=10) beta = pm.Normal('beta', mu=0, sd=10) z = alpha + pm.math.dot(x, beta) fs = pm.Deterministic('fs', 1 / (1 + pm.math.exp(-z))) bd = pm.Deterministic('bd', -alpha / beta) yl = pm.Bernoulli('yl', p=fs, observed=y) trace = pm.sample(5000) |
- 4行目:
 を定義する。
を定義する。 とした。
とした。 - 5行目:
 を定義する。
を定義する。 - 6行目:
 を定義する。
を定義する。 - 7行目:
 を定義する。
を定義する。 - 8行目:
 を定義する。
を定義する。 - 9行目:尤度
 を定義する。
を定義する。 - 10行目:MCMCを行う。
収束具合を見るため、次のコードでGelman-Rubinテストを行う。
|
1 |
pm.gelman_rubin(trace) |
計算される値は全て1.1未満となることを確認できる(結果は略)。1.1未満であれば収束したとみなして良い。次に、事後確率から算出される要約統計量を次のコードで計算する。
|
1 2 |
varnames = ['alpha', 'beta', 'bd'] pm.summary(trace, varnames) |
出力は以下の通り。
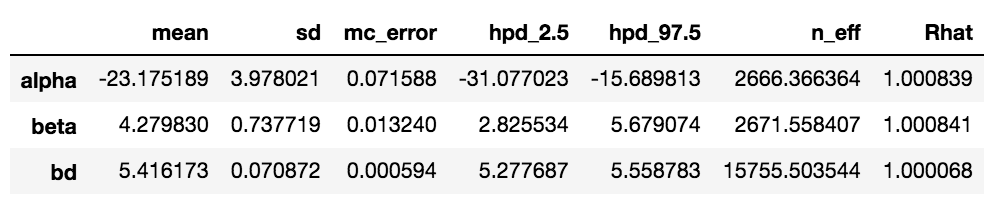
「mean」欄の「bd」の値5.42が、0と1を分ける境界線である。下図は、境界線の平均値とシグモイド関数の平均値を描画したものである。
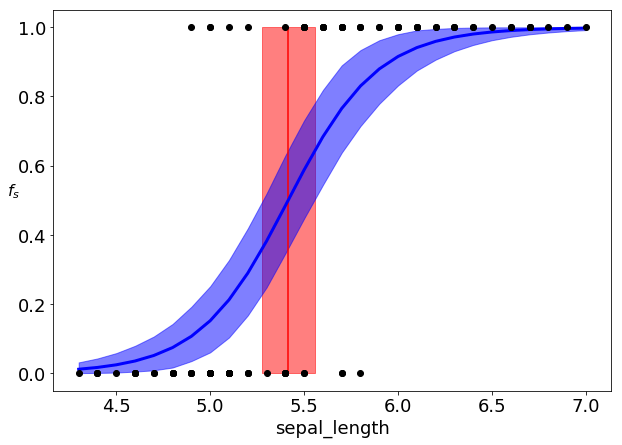
黒丸はsepal lengthの観測値(下側がsetosa)、濃い赤のラインが境界線![]() の平均値、薄い赤の領域が
の平均値、薄い赤の領域が![]() の95%HPDである。また、濃い青のラインがシグモイド関数
の95%HPDである。また、濃い青のラインがシグモイド関数![]() の平均値、薄い青の領域が
の平均値、薄い青の領域が![]() の95%HPDである。ある量が95%HPDの領域内にあるとは、95%の確率でその領域内に存在することを意味する。HPDはHighest Posterior Density(最高事後密度)の略である。
の95%HPDである。ある量が95%HPDの領域内にあるとは、95%の確率でその領域内に存在することを意味する。HPDはHighest Posterior Density(最高事後密度)の略である。
次に、生成モデルの場合を考える。コードは以下の通り。
|
1 2 3 4 5 6 7 |
with pm.Model() as model: mus = pm.Normal('mus', mu=0, sd=10, shape=2) sigma = pm.HalfNormal('sigma', sd=5) setosa = pm.Normal('setosa', mu=mus[0], sd=sigma, observed=x[:50]) versicolor = pm.Normal('versicolor', mu=mus[1], sd=sigma, observed=x[50:]) bd = pm.Deterministic('bd', (mus[0] + mus[1]) / 2) trace = pm.sample(5000) |
- 2行目:
 を定義する。
を定義する。 とした。
とした。 - 3行目:
 を定義する。
を定義する。 とした。
とした。 - 4,5行目:2つの分布
 と
と を定義する。
を定義する。 - 6行目:
 を定義する。
を定義する。 - 7行目:MCMCを行う。
先と同様に、Gelman-Rubinテストは合格する(詳細は略)。要約統計量は以下の通り。
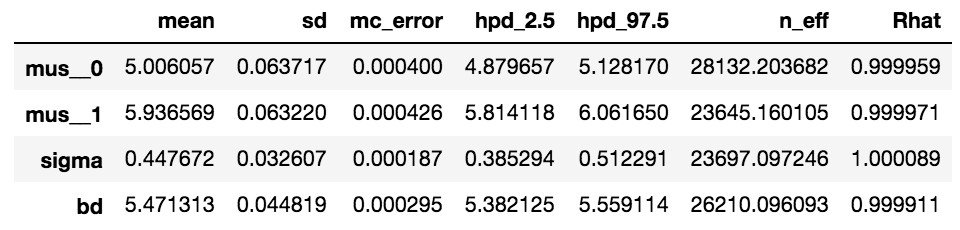
境界線の平均値は5.47程度になることが分かる。これは先に求めた識別モデルでの結果、5.42に近い値である。境界線の平均値と95%HPDを図示したものが下図である。
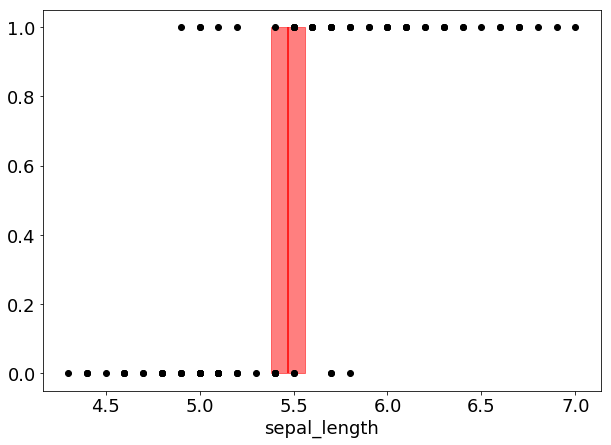
識別モデルでの結果に比べ、95%HPDが少し狭くなっている。すなわち、生成モデルの方が確からしさの高い値になる。
識別モデルと生成モデルの比較
識別モデルと生成モデルの違いは、それぞれの尤度を比較すると明確になる。すなわち、前者の尤度は![]() であり、これは
であり、これは![]() が観測されたときクラス
が観測されたときクラス![]() が実現する確率を表している。識別を行うと言う目的に直接アプローチする手法である。一方、後者では、その尤度
が実現する確率を表している。識別を行うと言う目的に直接アプローチする手法である。一方、後者では、その尤度![]() を見ても分かる通り、識別に直接アプローチせず、
を見ても分かる通り、識別に直接アプローチせず、![]() の分布を最初に求めるている。この分布を通して未知パラメータの事後分布を求めることで本来の目的である識別を行っている。生成モデルの場合、
の分布を最初に求めるている。この分布を通して未知パラメータの事後分布を求めることで本来の目的である識別を行っている。生成モデルの場合、![]() の分布が得られるので、擬似データの生成や、外れ値検知などにも応用することができる。
の分布が得られるので、擬似データの生成や、外れ値検知などにも応用することができる。
今回の例では、生成モデルの方が確度の高い境界線を得ることができた。その理由は、setosaとversicolorのサンプルが正規分布で良く近似できたためであると思われる。サンプルの分布が正規分布に従わない場合は、識別モデルの方が良いアプローチとなる。
今回生成モデルで用いた境界線![]() はとても簡単な式
はとても簡単な式![]() で表すことできた。その理由は、2つの正規分布の標準偏差を同じものとしたためである。サンプルの分布を正規分布とし、その標準偏差を等しくする解析手法を線形判別分析と呼ぶ。
で表すことできた。その理由は、2つの正規分布の標準偏差を同じものとしたためである。サンプルの分布を正規分布とし、その標準偏差を等しくする解析手法を線形判別分析と呼ぶ。

