はじめに
書籍「ベイズモデリングの世界」に「階層モデルで『個性』をとらえる」という解説がある。著者は北大の生態学を専門とする久保拓弥氏である。架空の植物を考え、その結実確率(胚珠が種子になる確率)を階層ベイズモデルを用いて推定する過程が分かりやすく解説されている。階層ベイズモデルのパラメータを推定する代表的な手法には、経験ベイズ法とMCMC法がある。久保氏の解説では前者を用いた推定がRを用いて行われている。MCMC法による解法の詳細には言及していないが、Rのサンプルプログラムへのリンクが記載されている。今回は、このサンプルプログラムと同じことを、前回紹介したPyMCを用いてなぞってみたい。今回使うのはPyMC3である(前回はPyMC2であった)。
ソースコード
今回実装したコードはここにあるsample_0.ipynbである。
問題設定
ここで取り上げる問題は以下の通り。
全ての個体が10個の種子を作れば、全種子数は![]() 、全ての個体がどれも種子を作らなければ全種子数は
、全ての個体がどれも種子を作らなければ全種子数は![]() になる。データはここからダウンロードできる。データの中身は以下の通り。
になる。データはここからダウンロードできる。データの中身は以下の通り。
“plant.ID”,”y”,”alpha”
1,0,-4.15958227809385
2,0,-3.71836219544951
3,0,-3.06901965190728
4,0,-3.05421060686106
5,0,-2.88065618323557
6,2,-2.70559527531842
7,1,-2.44170265669845
8,1,-2.22132654301567
…
解析に使う列は![]() である。この列には各個体の種子数が記載されている。横軸に種子数
である。この列には各個体の種子数が記載されている。横軸に種子数![]() 、縦軸に個体数
、縦軸に個体数![]() を取ると以下のグラフを得る。
を取ると以下のグラフを得る。
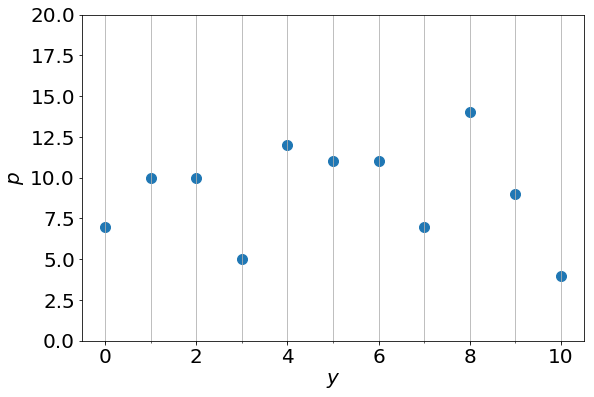
種子数0の個体数は7、種子数1の個体数は10であることなどが分かる。種子数0から10までの個体数を全て足すと100になることに注意する。
モデル化
ある1個体を考える。この個体が種子を![]() 個作る確率をモデル化したい。各個体には胚珠(種子の元になる器官)が10個あり、各胚珠は種子になるかならないかのどちらかである。従って、次の二項分布
個作る確率をモデル化したい。各個体には胚珠(種子の元になる器官)が10個あり、各胚珠は種子になるかならないかのどちらかである。従って、次の二項分布![]() で表すことができる。
で表すことができる。
(1) ![]()
ここで、![]() は胚珠が種子になる確率(結実確率)である。このとき、全ての観測データが実現する確率は
は胚珠が種子になる確率(結実確率)である。このとき、全ての観測データが実現する確率は
(2) 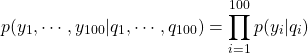
となる。
個体差を考慮しない予測
いま結実確率![]() が個体に寄らず一定であると仮定すると、対数尤度は
が個体に寄らず一定であると仮定すると、対数尤度は
(3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \ln{p(y_1,\cdots,y_{100}|q) &=& \sum_{i=1}^{100}\ln{p(y_i|q)}\\ &=& \sum_{i=1}^{100}\ln{{\rm Bin}(y_i|10,q)}\\ &=& \sum_{i=1}^{100}\left[y_i\ln{q}+(10-y_i)\ln{(1-q)} \right] + {\rm const.} \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-ad8bb5e37ca6db16253096dced4f35b9_l3.png)
となる。この式を![]() で微分することにより最尤推定値
で微分することにより最尤推定値![]() を得る。
を得る。
(4) 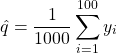
観測値を用いて![]() を計算すると0.496となる。このときの種子数と個体数の間の関係式は
を計算すると0.496となる。このときの種子数と個体数の間の関係式は
(5) ![]()
となり、対応するグラフは以下の点線となる。
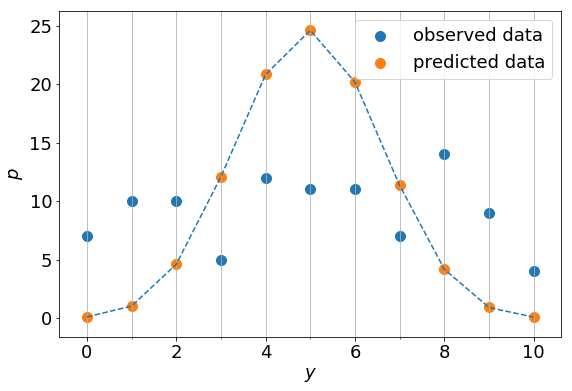
明らかに観測データを再現できていない。
ここまでの解析をPyMC3で行う。コードは以下の通り。
|
1 2 3 4 5 6 |
model = pm.Model() with model: q = pm.Uniform('q', lower=0, upper=1) y = pm.Binomial('y', n=10, p=q, observed=ys) map_estimate = pm.find_MAP(model=model) print(map_estimate['q']) |
lower=0からupper=1の範囲で定義される一様分布とした。observedに観測値をysを与える。qとyはmodelが必要とするstochastic変数である。PyMC2では、ユーザが明示的にこれらをModelのコンストラクタに渡していた。PyMC3では、上のコードのように、withの直下にモデルに必要な各種変数を記述すれば良い。上記の出力は以下の通り。
0.4960000053023121
先に示した値と同じである(![]() の事前分布として一様分布を与えたから、MAP推定値と最尤推定値は一致する)。
の事前分布として一様分布を与えたから、MAP推定値と最尤推定値は一致する)。
個体差を考慮する予測
(6) 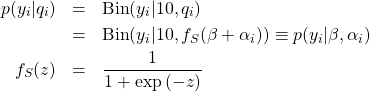
ここで、![]() はシグモイド関数である。
はシグモイド関数である。![]() は個体に依存しないパラメータを、
は個体に依存しないパラメータを、![]() は個体に依存するパラメータを表す。
は個体に依存するパラメータを表す。![]() と
と![]() について次の事前確率を定義する。
について次の事前確率を定義する。
(7) ![]()
ここで、![]() は平均
は平均![]() 、精度
、精度![]() の正規分布を表す(分散
の正規分布を表す(分散![]() の逆数を精度(precision)と呼ぶ)。個体に依存しない
の逆数を精度(precision)と呼ぶ)。個体に依存しない![]() については分散の大きな(
については分散の大きな(![]() )分布を考える。一方、個体に依存する
)分布を考える。一方、個体に依存する![]() に対しては、もう少し注意深く考察したい。そのため、次の事前確率を定義する。
に対しては、もう少し注意深く考察したい。そのため、次の事前確率を定義する。
(8) 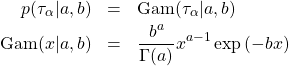
ここで、![]() はガンマ分布であり、これは正の実数を生成する。
はガンマ分布であり、これは正の実数を生成する。![]() を定数ではなく確率から生成される値とすることで、観測データに適応させて
を定数ではなく確率から生成される値とすることで、観測データに適応させて![]() を決めることができる(ただし、
を決めることができる(ただし、![]() と
と![]() はあらかじめ決めておくハイパーパラメータである)。このように事前分布のパラメータに対し、さらに事前分布を導入するモデルを階層ベイズモデルと呼ぶ。
はあらかじめ決めておくハイパーパラメータである)。このように事前分布のパラメータに対し、さらに事前分布を導入するモデルを階層ベイズモデルと呼ぶ。![]() 、
、![]() と置くと、求めたい事後分布は次式で与えられる。
と置くと、求めたい事後分布は次式で与えられる。
(9) ![]()
ここで、右辺分母は次式で計算される。
(10) 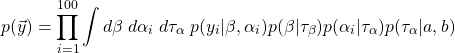
この積分は解析的に計算できないので、ここから先の計算はPyMC3を用いてMCMC法で近似する。コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 |
model = pm.Model() with model: beta = pm.Normal('beta', mu=0, tau=1.0e-2) tau = pm.Gamma('tau', alpha=1.0e-02, beta=1.0e-02) alpha = pm.Normal('alpha', mu=0, tau=tau , shape=len(ys)) ymu = pm.math.sigmoid(beta + alpha) y = pm.Binomial('y', n=10, p=ymu, observed=ys) start = pm.find_MAP() step = pm.NUTS() trace = pm.sample(5000, start=start, step=step) |
taualphabetashapeobservedには観測値ysを与える。上のコードを実行したあと、以下のコードで収束しているか否かを判定する。
|
1 2 |
# 収束をチェックする。 pm.gelman_rubin(trace) |
出力は以下の通り。
{‘alpha’: array([0.99992116, 0.99997074, 0.99997656, 1.00101515, 1.0000671 ,
0.99997194, 0.99990008, 1.00046983, 0.99990016, 1.00004488,
0.99997887, 0.99996494, 1.00001114, 0.99993037, 1.00009044,
0.9999153 , 0.99990012, 0.99999316, 0.99990019, 0.99990849,
0.9999183 , 1.00019395, 0.99997166, 0.99990267, 1.00025804,
1.00006084, 1.00003207, 1.00001905, 1.00002649, 0.99999359,
0.99991317, 0.99990444, 1.00010107, 1.00044065, 1.00008226,
0.9999002 , 0.99991316, 0.99995332, 1.00016158, 1.00016238,
0.99991051, 0.99994176, 1.00003935, 0.99997246, 1.00052741,
1.00017737, 0.99995378, 1.00002957, 1.00018027, 0.99999548,
1.00012819, 0.99990123, 0.99993936, 0.99992739, 0.99991631,
0.9999227 , 0.9999047 , 1.00006704, 0.99997697, 0.99992804,
0.9999103 , 0.99990415, 0.99991652, 0.99991608, 1.00098608,
0.99990014, 0.99990024, 0.9999914 , 1.00003664, 0.99991117,
0.99990698, 0.99997845, 0.99991626, 0.99992411, 1.00014929,
0.9999008 , 0.9999 , 0.99992404, 0.99990093, 0.99990898,
1.00012367, 1.00011088, 0.99995555, 0.99991072, 0.99992426,
1.00033826, 1.00004621, 0.99990063, 0.99991521, 1.00011476,
1.00005838, 0.99990038, 0.99991504, 0.99990287, 0.99991835,
1.00019647, 0.99993153, 0.99993019, 0.99995296, 1.00004081]),
‘beta’: 0.9999865601392494,
‘tau’: 1.0006839287826985}
100個の![]() と
と![]() 、
、![]() のGelman-Rubin統計量
のGelman-Rubin統計量![]() が出力される。詳細は省くが、経験則から
が出力される。詳細は省くが、経験則から![]() のとき収束したとみなして良い。上の結果を見ると全変数が1.1未満となっていることが分かる。ここまでの作業で、式(9)で定義される事後確率が求まったことになる。この事後確率を用いると、予測される種子数
のとき収束したとみなして良い。上の結果を見ると全変数が1.1未満となっていることが分かる。ここまでの作業で、式(9)で定義される事後確率が求まったことになる。この事後確率を用いると、予測される種子数![]() の分布は次式で計算される。
の分布は次式で計算される。
(11) 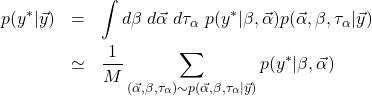
和は事後確率からサンプリングした点を用いて行えば良い。![]() はサンプル点の総数である。この計算を行うコードは以下の通り。
はサンプル点の総数である。この計算を行うコードは以下の通り。
|
1 2 3 4 |
sample_size, _ = trace['alpha'].shape posterior = pm.sample_ppc(trace, sample_size, model=model) y_posterior = posterior['y'] |
これだけのコードで![]() からサンプリングされた点を得ることができる。 このサンプル点からヒストグラムを作れば、
からサンプリングされた点を得ることができる。 このサンプル点からヒストグラムを作れば、![]() の予測分布を得ることができる。
の予測分布を得ることができる。
|
1 2 3 4 5 6 7 8 9 |
# sample_sizeの数だけヒストグラムを作る。 pred_ys = np.empty((sample_size, bins)) for i, k in enumerate(y_posterior): pred_ys[i] = np.histogram(k, bins)[0] # 平均をとる。 pred_ys = pred_ys.mean(axis=0) # 標準偏差を計算する。 pred_std = pred_ys.std(axis=0) |
次のコードで描画する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 |
# 描画する。 plt.figure(figsize=(10,6)) plt.rcParams['font.size'] = 16 plt.scatter(xs, histo_ys, s=100, label='observed data') plt.plot(xs, binom_ys, ls='--') plt.scatter(xs, binom_ys, s=100, label='fixed $q 以下に結果を示す。 <img src="/wp-content/uploads/2018/09/fig4.png" alt="" width="623" height="386" class="aligncenter size-full wp-image-5975"> 凡例の意味は以下の通り。 <nl></nl> <li>青色の丸:観測値</li> <li>橙色の丸(点線):結実確率に個体差がないと仮定した場合の分布</li> <li>緑色の丸:結実確率に個体差があると仮定した場合の分布(平均値)</li> <li>青色の領域:[latex]\sigma[/latex](標準偏差)の範囲</li> <li>黄色の領域:[latex]2\sigma[/latex]の範囲</li> 結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。 <h2 class="category_header left"><span class="inner left">まとめ</span></h2> 今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度[latex]p(y|\beta,\alpha_i)[/latex]に対し、パラメータ[latex]\beta[/latex]と[latex]\alpha_i[/latex]の事前確率を仮定する。後者の事前確率に含まれるパラメータ[latex]\tau_{\alpha}[/latex]に対し、さらに事前確率を導入することにより、[latex]\alpha_i[/latex]を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。 今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである<a href="https://medium.com/@pymc_devs/theano-tensorflow-and-the-future-of-pymc-6c9987bb19d5" target="_blank" rel="nofollow noopener noreferrer">(引用元)</a>。 ) plt.xlabel('$y 以下に結果を示す。 <img src="/wp-content/uploads/2018/09/fig4.png" alt="" width="623" height="386" class="aligncenter size-full wp-image-5975"> 凡例の意味は以下の通り。 <nl></nl> <li>青色の丸:観測値</li> <li>橙色の丸(点線):結実確率に個体差がないと仮定した場合の分布</li> <li>緑色の丸:結実確率に個体差があると仮定した場合の分布(平均値)</li> <li>青色の領域:[latex]\sigma[/latex](標準偏差)の範囲</li> <li>黄色の領域:[latex]2\sigma[/latex]の範囲</li> 結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。 <h2 class="category_header left"><span class="inner left">まとめ</span></h2> 今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度[latex]p(y|\beta,\alpha_i)[/latex]に対し、パラメータ[latex]\beta[/latex]と[latex]\alpha_i[/latex]の事前確率を仮定する。後者の事前確率に含まれるパラメータ[latex]\tau_{\alpha}[/latex]に対し、さらに事前確率を導入することにより、[latex]\alpha_i[/latex]を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。 今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである<a href="https://medium.com/@pymc_devs/theano-tensorflow-and-the-future-of-pymc-6c9987bb19d5" target="_blank" rel="nofollow noopener noreferrer">(引用元)</a>。 ) plt.ylabel('$p 以下に結果を示す。 <img src="/wp-content/uploads/2018/09/fig4.png" alt="" width="623" height="386" class="aligncenter size-full wp-image-5975"> 凡例の意味は以下の通り。 <nl></nl> <li>青色の丸:観測値</li> <li>橙色の丸(点線):結実確率に個体差がないと仮定した場合の分布</li> <li>緑色の丸:結実確率に個体差があると仮定した場合の分布(平均値)</li> <li>青色の領域:[latex]\sigma[/latex](標準偏差)の範囲</li> <li>黄色の領域:[latex]2\sigma[/latex]の範囲</li> 結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。 <h2 class="category_header left"><span class="inner left">まとめ</span></h2> 今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度[latex]p(y|\beta,\alpha_i)[/latex]に対し、パラメータ[latex]\beta[/latex]と[latex]\alpha_i[/latex]の事前確率を仮定する。後者の事前確率に含まれるパラメータ[latex]\tau_{\alpha}[/latex]に対し、さらに事前確率を導入することにより、[latex]\alpha_i[/latex]を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。 今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである<a href="https://medium.com/@pymc_devs/theano-tensorflow-and-the-future-of-pymc-6c9987bb19d5" target="_blank" rel="nofollow noopener noreferrer">(引用元)</a>。 ) plt.plot(xs, pred_mean, ls='-.', c='g') plt.scatter(xs, pred_mean, s=100, label='non-fixed $q$(mean)') plt.fill_between(xs, pred_mean - 2*pred_std, pred_mean + 2*pred_std, color='yellow', alpha=0.2, label='$\pm2\sigma 以下に結果を示す。 <img src="/wp-content/uploads/2018/09/fig4.png" alt="" width="623" height="386" class="aligncenter size-full wp-image-5975"> 凡例の意味は以下の通り。 <nl></nl> <li>青色の丸:観測値</li> <li>橙色の丸(点線):結実確率に個体差がないと仮定した場合の分布</li> <li>緑色の丸:結実確率に個体差があると仮定した場合の分布(平均値)</li> <li>青色の領域:[latex]\sigma[/latex](標準偏差)の範囲</li> <li>黄色の領域:[latex]2\sigma[/latex]の範囲</li> 結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。 <h2 class="category_header left"><span class="inner left">まとめ</span></h2> 今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度[latex]p(y|\beta,\alpha_i)[/latex]に対し、パラメータ[latex]\beta[/latex]と[latex]\alpha_i[/latex]の事前確率を仮定する。後者の事前確率に含まれるパラメータ[latex]\tau_{\alpha}[/latex]に対し、さらに事前確率を導入することにより、[latex]\alpha_i[/latex]を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。 今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである<a href="https://medium.com/@pymc_devs/theano-tensorflow-and-the-future-of-pymc-6c9987bb19d5" target="_blank" rel="nofollow noopener noreferrer">(引用元)</a>。 ) plt.fill_between(xs, pred_mean - pred_std, pred_mean + pred_std, color='blue', alpha=0.2, label='$\pm\sigma 以下に結果を示す。 <img src="/wp-content/uploads/2018/09/fig4.png" alt="" width="623" height="386" class="aligncenter size-full wp-image-5975"> 凡例の意味は以下の通り。 <nl></nl> <li>青色の丸:観測値</li> <li>橙色の丸(点線):結実確率に個体差がないと仮定した場合の分布</li> <li>緑色の丸:結実確率に個体差があると仮定した場合の分布(平均値)</li> <li>青色の領域:[latex]\sigma[/latex](標準偏差)の範囲</li> <li>黄色の領域:[latex]2\sigma[/latex]の範囲</li> 結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。 <h2 class="category_header left"><span class="inner left">まとめ</span></h2> 今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度[latex]p(y|\beta,\alpha_i)[/latex]に対し、パラメータ[latex]\beta[/latex]と[latex]\alpha_i[/latex]の事前確率を仮定する。後者の事前確率に含まれるパラメータ[latex]\tau_{\alpha}[/latex]に対し、さらに事前確率を導入することにより、[latex]\alpha_i[/latex]を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。 今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである<a href="https://medium.com/@pymc_devs/theano-tensorflow-and-the-future-of-pymc-6c9987bb19d5" target="_blank" rel="nofollow noopener noreferrer">(引用元)</a>。 ) plt.gca().xaxis.set_minor_locator(tick.MultipleLocator(1)) plt.grid(which='minor') plt.legend(loc='upper left') plt.show() |
以下に結果を示す。
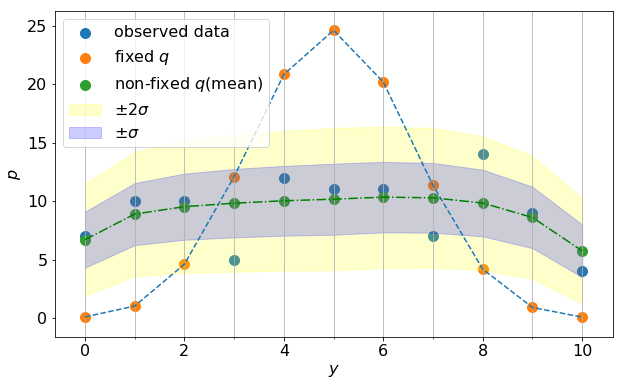
凡例の意味は以下の通り。
結実確率に個体差を考慮することにより、観測データをかなり良く再現できるようになることが分かる。
まとめ
今回は、階層ベイズモデルにより、個体差を取り込む手順を示した。尤度![]() に対し、パラメータ
に対し、パラメータ![]() と
と![]() の事前確率を仮定する。後者の事前確率に含まれるパラメータ
の事前確率を仮定する。後者の事前確率に含まれるパラメータ![]() に対し、さらに事前確率を導入することにより、
に対し、さらに事前確率を導入することにより、![]() を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。
を単なる主観ではなく観測データに適応させて決めることができるようになる。すなわち、観測データから個体差を抽出することができるのである。
今回の解析ではPyMC3を用いた。前回使用したPyMC2よりモデルを記述しやすくなっている。また、PyMC3ではバックエンドにTheanoが使われており、速度面でも改善が見られる。ご存知のようにTheanoは最近メンテナンスを停止する旨の告知がなされた。PyMC3の開発チームは、PyMC3のバックエンドとして必要となる機能だけではあるが、メンテナンスを引き継ぐようである。また、それと並行してPyMC4の開発が進められている。こちらのバックエンドはTensorFlow Probabilityなるモジュールを使うようだ。PyMC4のリリースはまだまだ先であり、今後もPyMC3の機能拡張やバグフィックスが続けられるとのことである(引用元)。

