はじめに
前回、ガウス過程の理論を解説した。今回はPyMC3を用いて実際に計算を行ってみる。ガウス過程の計算では、パラメータを含むカーネルをあらかじめ「主観的」に設定し、観測データを用いてこのパラメータを推定する。パラメータを推定する手法として、最尤推定法、事後確率最大化法、ベイズ推定法がある。今回はベイズ推定を行う。
ベイズ推定による定式化
回帰問題を考える。観測値を![]() 、パラメータを
、パラメータを![]() として、これらの同時確率分布
として、これらの同時確率分布![]() から次式を得る。
から次式を得る。
(1) ![]()
適当な尤度![]() と事前確率
と事前確率![]() を設定し、事後確率
を設定し、事後確率![]() を求めることがベイズ推定の目的である。いま
を求めることがベイズ推定の目的である。いま
(2) ![]()
とおき、パラメータ![]() をカーネルに関わる部分
をカーネルに関わる部分![]() とそうでない部分
とそうでない部分![]() の2つに分離する。さらに、
の2つに分離する。さらに、![]() と
と![]() の間に次式を仮定する。
の間に次式を仮定する。
(3) ![]()
ここで、![]() は平均
は平均![]() 、分散
、分散![]() の正規分布を表す。各観測値は独立同分布から生成されると仮定すると、尤度は
の正規分布を表す。各観測値は独立同分布から生成されると仮定すると、尤度は
(4) 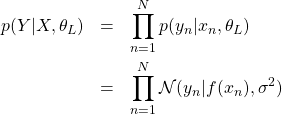
と書くことができる。ここで、![]() とした。
とした。![]() の事前分布として
の事前分布として![]() を、関数
を、関数![]() の事前分布として次のガウス過程を仮定する。
の事前分布として次のガウス過程を仮定する。
(5) ![]()
ここで、![]() とした。
とした。![]() は
は![]() 次元のゼロベクトル、
次元のゼロベクトル、![]() はパラメータ
はパラメータ![]() を持つ
を持つ![]() の共分散行列、その成分
の共分散行列、その成分![]() がカーネル関数となる。さらに、
がカーネル関数となる。さらに、![]() の事前分布として
の事前分布として![]() も導入する。ここまでの結果をまとめると、式(1)は次のようになる。
も導入する。ここまでの結果をまとめると、式(1)は次のようになる。
(6) ![]()
![]() の事前分布
の事前分布![]() がガウス過程であることに注意する。上の式の右辺をベイズ推定で評価し、事後確率
がガウス過程であることに注意する。上の式の右辺をベイズ推定で評価し、事後確率![]() を求める。これらを用いると、未知の値
を求める。これらを用いると、未知の値![]() に対する
に対する![]() の確率分布を次式により計算することができる。
の確率分布を次式により計算することができる。
(7) ![]()
右辺の積分内の最初の項![]() は
は![]() を表し、式(5)から解析的に求めることができる条件付き確率分布である。上式から
を表し、式(5)から解析的に求めることができる条件付き確率分布である。上式から![]() の分布が分かれば、未知の値
の分布が分かれば、未知の値![]() に対する
に対する![]() の値は次式から決定することができる。
の値は次式から決定することができる。
(8) 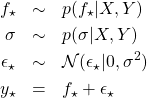
以上で定式化できたので、実際に計算を行う。
ソースの場所
今回のソースはここのsample_pymc3_latent.ipynbである。
データの生成
人工的に生成した以下のデータを使う。
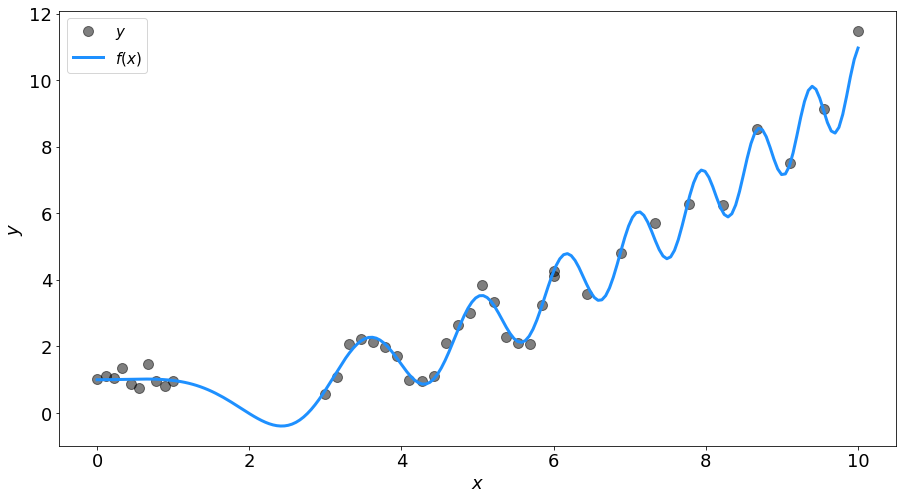
計算式は以下の通り。
(9) 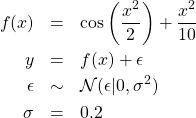
PyMC3による計算
ベイズ推定のコードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
with pm.Model() as model: ℓ = pm.Gamma("ℓ", alpha=2, beta=1) η = pm.HalfCauchy("η", beta=5) cov = η**2 * pm.gp.cov.Matern52(1, ℓ) gp = pm.gp.Latent(cov_func=cov) f = gp.prior("f", X=observed_xs) σ = pm.HalfCauchy("σ", beta=5) ν = pm.Gamma("ν", alpha=2, beta=0.1) y_ = pm.StudentT("y", mu=f, lam=1.0/σ, nu=ν, observed=observed_ys) trace = pm.sample(1000) |
- 2行目から4行目まででカーネルを定義する。
 と
と はカーネルパラメータ
はカーネルパラメータ に相当する。このパラメータに対しても事前分布(ガンマ分布、半コーシ分布)を設定していることに注意する。
に相当する。このパラメータに対しても事前分布(ガンマ分布、半コーシ分布)を設定していることに注意する。 - 6行目で式(5)のガウス過程
 を定義する。
を定義する。 - 10行目から12行目までで式(4)の尤度を定義する。上の定式化では尤度としてガウス分布を用いたが、コードではスチューデントのt分布を用いた。外れ値に強いためである。この分布のパラメータ
 に対しても事前分布を定義する。パラメータ
に対しても事前分布を定義する。パラメータ が
が に相当する。
に相当する。 - 14行目でMCMCを実行する。
上の計算のあと次のコードで未知データ![]() に対する
に対する![]() の分布を計算する。
の分布を計算する。
|
1 2 3 4 5 6 |
n_new = 200 X_new = np.linspace(0, 15, n_new)[:,None] with model: f_pred = gp.conditional("f_pred", X_new) pred_samples = pm.sample_posterior_predictive(trace, vars=[f_pred], samples=1000) |
- 1行目と2行目で未知データ
 を作成する。
を作成する。 - 5行目で条件付き確率
 が設定される。
が設定される。 - 6行目で、この条件付き確率と
trace内に格納されている各種事後確率を用いて、式(7)で与えた が計算される。
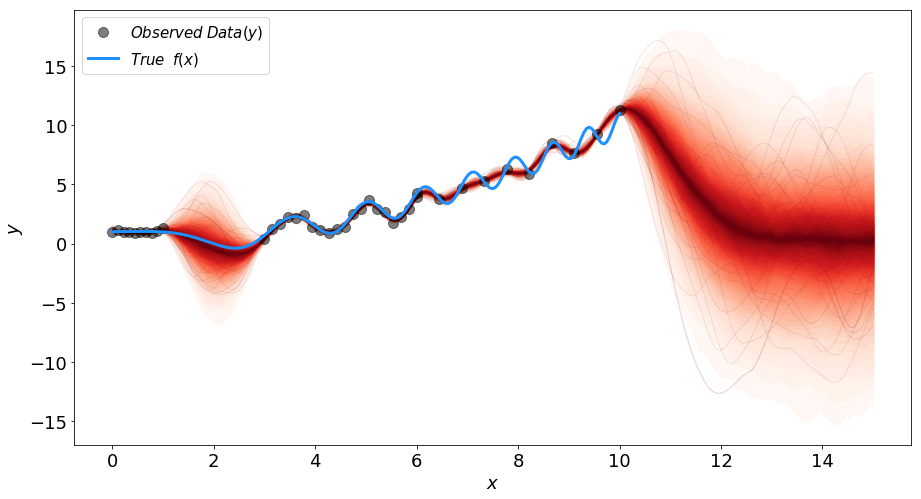
が計算される。samplesは生成する曲線 の数。結果は以下の通り
の数。結果は以下の通り

生成された1000本の曲線を赤で示した。赤の濃さは曲線の密度を表し、曲線の揺れ幅が予測の不確かさを表す。データの密度が高い場所では不確かさは小さく、データの密度が低い場所では不確かさは大きくなる。まとめ
ガウス過程による回帰の計算は、PyMC3を用いれば容易に実行することができることを示した。また、式とコードを明確に関連付けた。理論式と対応づけることで理解を深めることができる。
ガウス過程で重要となるのは、カーネルとして何を設定すべきかという点である。上のコードではPyMC3のチュートリアルで紹介されているカーネルをそのまま用いた。チュートリアルを読むと、どのカーネルを選択すべきかのおおよその目安は分かる。カーネルの選択についての解説は機会を改めたい。参照文献
- Pythonによるベイズ統計モデリング 良書ですが、理論式との対応付けが明確でないので何を計算しているのか分からなくなることがある。
- PyMC3