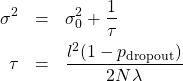はじめに
dropoutを持つネットワークを用いると、Bayes推論のように「不確実さ(uncertainty)」を評価できることを示す。
Bayes推論
最初に、「不確実さ」まで評価できる手法であるBayes推論の概要を、回帰問題を例に取りまとめる。
いま、![]() が観測されているとする。
が観測されているとする。![]() が説明変数、
が説明変数、![]() が目的変数である。このとき、潜在変数
が目的変数である。このとき、潜在変数![]() を導入し、同時確率分布
を導入し、同時確率分布![]() を考える。この分布にBayesの定理を適用すると次式を得る。
を考える。この分布にBayesの定理を適用すると次式を得る。
(1) ![]()
ただし、式変形の途中で、![]() を用いた。
を用いた。![]() は潜在変数に依存しない観測値である。式(1)の左辺にある
は潜在変数に依存しない観測値である。式(1)の左辺にある![]() を事後分布、右辺の分子にある
を事後分布、右辺の分子にある![]() を尤度、
を尤度、![]() を事前分布、右辺分母にある
を事前分布、右辺分母にある![]() をモデルエビデンスと呼ぶ。事後分布
をモデルエビデンスと呼ぶ。事後分布![]() を求めることができれば、次式により、未観測の説明変数
を求めることができれば、次式により、未観測の説明変数![]() が与えられた時の目的変数
が与えられた時の目的変数![]() の条件付き確率分布を求めることができる。
の条件付き確率分布を求めることができる。
(2) ![]()
下図は式(2)を用いて予測を行った具体例である(このグラフの導出は次回行う)。
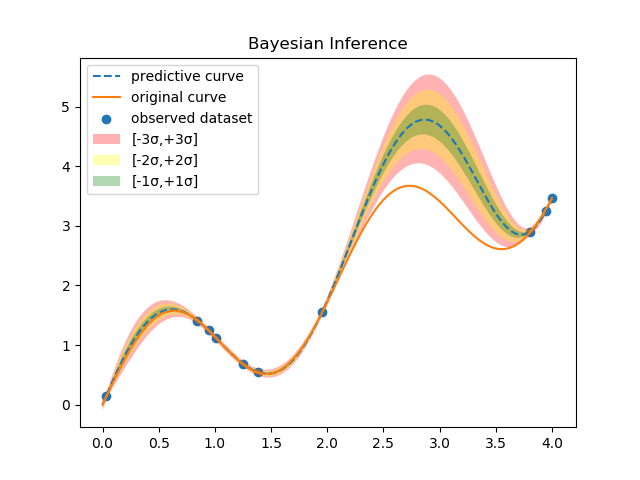
橙色の実線がGround Truthとなる曲線、青丸が適当にサンプルした観測値(10個)、破線が予測曲線である。色ぬりした領域が標準偏差の大きさ、すなわち予測値の不確実さを表す。この図から分かる通り、観測値近傍の標準偏差は小さく、観測値が存在しない領域の標準偏差は大きくなる。Bayes推論の優れた点は、各予測値を点として求めるだけでなく、その確からしさも定量的に導出することができることである。式(2)を計算するためには、事後分布![]() を求める必要がある。Bayes推論の目的はこの事後分布を解析的あるいは近似的に求めることである。
を求める必要がある。Bayes推論の目的はこの事後分布を解析的あるいは近似的に求めることである。
次に掲げる文献は、Bayes推論をdropoutを持つネットワークで再現できることを示したものである。
「原論文」は博士論文なので長大であり、簡単に読めるものではない。「原論文著者による解説」には、dropoutを持つネットワークから不確実さを計算する手順が簡潔にまとめられている。また、「原論文」の大凡の理屈は日本語解説により理解することができる。一言で言うと、Bayes推論で使われる変分推論を用いると、ある最小化すべき式を得る。この式が、dropoutを含むネットワークの損失関数と等価になるというものである。dropoutで考慮される確率的要素が、変分推論で最小化すべき式とネットワークの損失関数とを結びつけている。
計算手順
回帰問題をニューラルネットワークを用いて考え、上の解説を参照して実際に不確実さを求める。手順は以下の通りである。
- 適当な層を持つネットワークを作る。その際、dropoutと
 正則化項を取り入れておく。
正則化項を取り入れておく。 - 通常通り訓練を行い、訓練済みモデルを作る。
- dropoutの効果をオンにしたまま予測を行う。通常なら予測時はこの効果はオフにするが、ここではオンにしたまま計算する。
- 予測を複数回行い、その平均値
 と分散
と分散 を計算する。
を計算する。 - 次式を計算する。
(3)

ここで、
 はlength scaleと著者らが呼んでいる量、
はlength scaleと著者らが呼んでいる量、 はユニットを0にする確率、
はユニットを0にする確率、 は観測値の数、
は観測値の数、 は正則化項につける係数である。
は正則化項につける係数である。 が求めたい分散(不確実さ)である。
が求めたい分散(不確実さ)である。
コードの場所
今回のコードはここにある。いつものようにChainerを用いた。
ネットワークの構造
今回のネットワークの構造を示す(train.py)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
class MyNet(chainer.Chain): def __init__(self, length_scale, d_in, h, d_out, dropout_ratio=0.5, train=True): W = initializers.HeNormal(1 / length_scale) bias = initializers.Zero() super(MyNet, self).__init__() with self.init_scope(): self.linear1 = L.Linear(d_in, h, initialW=W, initial_bias=bias) self.linear2 = L.Linear(h, h, initialW=W, initial_bias=bias) self.linear3 = L.Linear(h, h, initialW=W, initial_bias=bias) self.linear4 = L.Linear(h, d_out, initialW=W, initial_bias=bias) self.train = train self.dropout_ratio = dropout_ratio def __call__(self, x): h = F.dropout(x, ratio=self.dropout_ratio) h = self.linear1(x) h = F.relu(h) h = F.dropout(h, ratio=self.dropout_ratio) h = self.linear2(h) h = F.relu(h) h = F.dropout(h, ratio=self.dropout_ratio) h = self.linear3(h) h = F.relu(h) h = F.dropout(h, ratio=self.dropout_ratio) h = self.linear4(h) return h |
4層のネットワークである。それぞれの層にdropoutを適用していることに注意する。![]() 正則化項は以下で取り入れることができる(train.py)。
正則化項は以下で取り入れることができる(train.py)。
|
1 |
optimizer.add_hook(chainer.optimizer.WeightDecay(rate=WEIGHT_DECAY)) |
実験
Ground Truthとなる曲線としてガウス関数を2つ重ねたものを使用した。観測値の個数![]() 、
、![]() 、
、![]() である。
である。![]() はGround Truthの曲線の変化を捉える程度の長さで良いようなので10とした。以下に計算結果を示す。予測は100回行い、平均値
はGround Truthの曲線の変化を捉える程度の長さで良いようなので10とした。以下に計算結果を示す。予測は100回行い、平均値![]() と分散
と分散![]() の計算を行った。
の計算を行った。
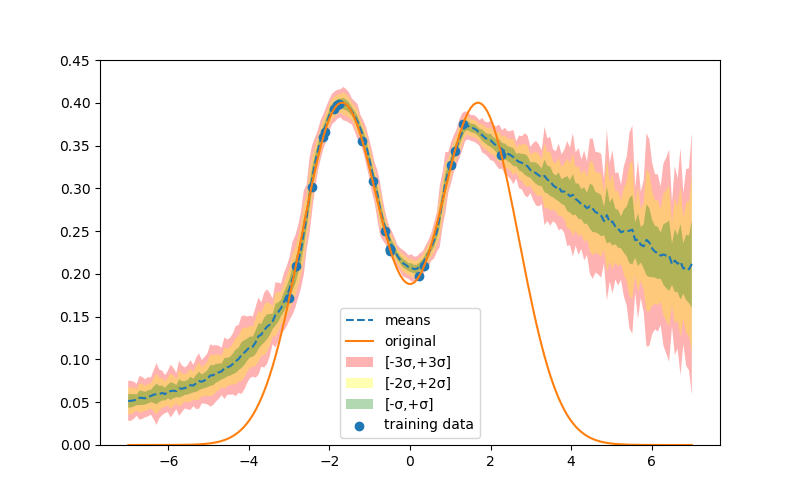
実線がGround Truthの曲線、青丸が観測値(20個)、点線が平均値![]() 、色ぬりが標準偏差
、色ぬりが標準偏差![]() である。Bayes推論の説明時に示したグラフと同様に、観測値が存在しない領域の標準偏差が大きくなっていることが分かる。
である。Bayes推論の説明時に示したグラフと同様に、観測値が存在しない領域の標準偏差が大きくなっていることが分かる。
まとめ
Bayes推論では確率分布を求めることが目的なので、自動的に予測値の確からしさを知ることができる。一方、深層学習が予測する値は「点」であり、その確からしさは評価されない。今回紹介した文献は、ほとんどの深層学習に使われているdropoutを利用することで、点推定を与える深層学習から不確かさを導出できることを示している。大変興味深い研究である。
補足
本稿を含め、これから数回に渡ってBayes推論に関わる話題を取り上げる予定である。今回は初回なのでBayes主義による確率の考え方について解説しておく。
ある理論物理学者が![]() という新しい理論を発表した。この理論が正しい確率を
という新しい理論を発表した。この理論が正しい確率を![]() とおく。後日、実験
とおく。後日、実験![]() が行われた。この実験を受けて理論
が行われた。この実験を受けて理論![]() が正しい確率は
が正しい確率は![]() に更新される。
に更新される。![]() は事前確率、
は事前確率、![]() は事後確率である。実験が繰り返されるごとに
は事後確率である。実験が繰り返されるごとに![]() が正しい確率は更新されていく(
が正しい確率は更新されていく(![]() )。このように新しい事実・証拠を受け入れることにより、事前確率(事前知識)の確からしさ(確率)を更新していく考え方をBayes主義と呼ぶ。ところで、確率には別の捉え方もある。長期間に渡って事象
)。このように新しい事実・証拠を受け入れることにより、事前確率(事前知識)の確からしさ(確率)を更新していく考え方をBayes主義と呼ぶ。ところで、確率には別の捉え方もある。長期間に渡って事象![]() が起きた回数(ここの例で言えば理論
が起きた回数(ここの例で言えば理論![]() が正しかった回数)を実際に数える立場である。これを頻度主義と呼ぶ。Bayes主義の場合、最初の確率
が正しかった回数)を実際に数える立場である。これを頻度主義と呼ぶ。Bayes主義の場合、最初の確率![]() はその学者の主観あるいは信念(belief)である。この信念が実験を繰り返すごとに客観的事実として認知されていくことになる。最初の頃はその理論の不確かさは大きかったが、徐々に不確かさが小さくなっていく。一方、頻度主義の場合は、最初から客観的事実として確率を捉えようとする。これら2つの考え方は相容れないものではない。Bayes主義的な確率は事実・証拠の数が増えるにつれて、頻度主義による確率に漸近していく。
はその学者の主観あるいは信念(belief)である。この信念が実験を繰り返すごとに客観的事実として認知されていくことになる。最初の頃はその理論の不確かさは大きかったが、徐々に不確かさが小さくなっていく。一方、頻度主義の場合は、最初から客観的事実として確率を捉えようとする。これら2つの考え方は相容れないものではない。Bayes主義的な確率は事実・証拠の数が増えるにつれて、頻度主義による確率に漸近していく。
最初は信念であるが、事実・証拠が得られたら、信念を更新していく。更新が繰り返されるごとにその信念は、客観的事実に近づいていく。これがBayes主義の立場である。