はじめに
最近、Graph Convolutionが盛り上がってきているように思いますので、今回は少し古いですが、DeepWalkの解説をしてみたいと思います。
DeepWalkはGraph Embeddingの先駆けとなったもので、2014年に提案された手法です。
DeepWalk
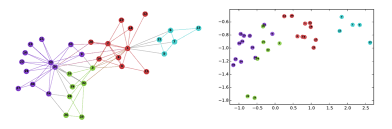
この手法により、グラフのベクトル表現を得ることができます。DeepWalkによって、Fig.1の左図のようなグラフで表現されたものを、Fig.1の右図のようにうまくベクトルで表現できます。“うまく”とは、グラフの特徴を捉えて右図のように関係性が近いもの同士を配置できることです。
Karate Networkとはある大学の空手部のソーシャルネットワークをモデルとしていて、誰と誰が部活以外で会うなどの関係を表したソーシャルネットワークです。
Karate Network
Fig.1 Karate Networkのネットワーク構造とDeepWalkで処理されたKarate Network
DeepWalkより引用
そもそもグラフとは?
ここで表しているグラフとは2次元平面に描かれていて、何かと何かがリンクして関係を持っていることなどを表現するためのネットワーク構造を指します。
グラフ上の図でいうと丸い部分をノードといい、ノードとノードをつなげているものをエッジといいます。エッジには方向があるグラフを有向グラフといい、方向がないグラフを無向グラフといいます。上図のようにエッジのつながり方は色々で、ノード同士がエッジで接続されていますが、そのエッジが自分自身に向いているものや、また複数のノードと接続されることもあります。グラフは身の回りで言うと、上にあるKarate Networkのようなソーシャルネットワーク、化学式など多種多様なものの関係性をグラフで表現できます。
グラフ解析の難しさ
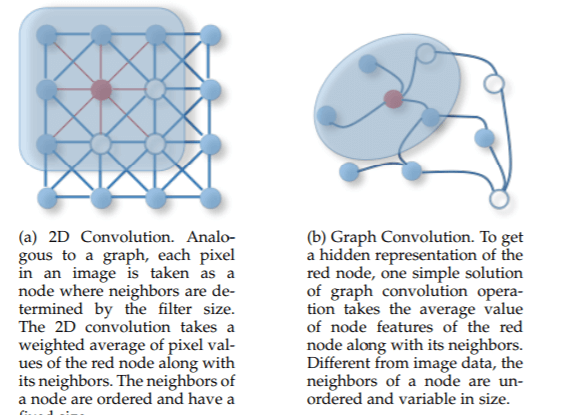
グラフでリッチな表現をできるので、機械学習のアルゴリズムを使って何か分析・予測をしたい気持ちになりますが、従来の機械学習のアルゴリズムを使って解析することは、非常に難しかったといわれています。その理由は主に、グラフをそのままの定義でCNNを適応させることができないことが挙げられます。画像などとは異なり、グラフは規則的ではありません。例えば画像の場合、Fig.2の左図のようにピクセルを規則的にグリッド上に配置できます。しかしそもそもグラフの場合、Fig.2の右図のように、孤立したノードもあれば、複数のノードへ接続されているなど、複雑にノードが絡み合っていて、注目するノードによってノードが不規則に接続しているため、このままではCNNを利用することができません。
Fig.2 画像に対する畳み込みとグラフに対する畳み込みの違い
A Comprehensive Survey on Graph Neural Networksより引用
グラフは色々な関係性をうまく表現できるのですが、この問題を解決しなければ機械学習のアルゴリズムなどを用いた解析はできません。しかし、DeepWalkはこの問題に立ち向かう手法です。
ランダムウォーク
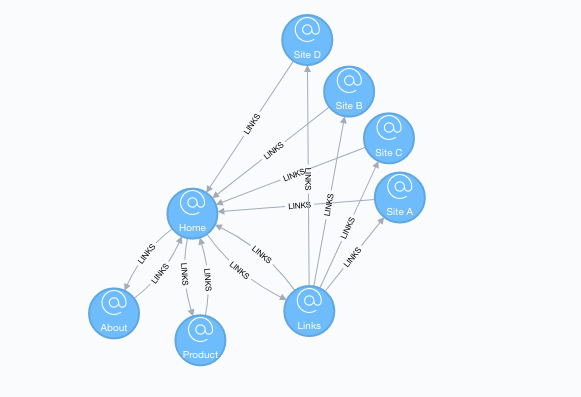
ランダムウォークは、グラフのあるノードから出発してその近傍へランダムに移動する確率的な操作です。DeepWalkではこのランダムウォークをある回数だけ行い、ランダムウォークで訪れたノードを系列データとして取得します。
Fig.3にランダムウォークのイメージを載せました。注目するノードをFig.3のHomeとすると、Homeから移動できるノードである’About’, ‘Product’, ‘Links’のいずれかへ確率的に移動します。
Fig.3 ランダムウォークのイメージ
The Random Walk algorithmより引用
Skip-gram
Skip-gramとは自然言語処理で使われるアルゴリズムの1つで、ある単語が与えられたときにその周辺語を得ることができます。ベクトル化することで、似ている単語や正反対の単語などを区別することができます。(計算の高速化などの詳しい説明は、省略させていただきます。)
今、I have a penというフレーズに関してSkip-gramを適応させたいとします。
この文においてまず、{ I }という単語に注目します。{ I }の次に来る単語は動詞の{ have }ですが、Iの次に{ a }や{ pen }が来ることは英語の文法では、考えられません。すなわち、{ I }の後ろに来る単語には{ have }が来る可能性が十分高いと解釈できます。このロジックで、Skip-gramは入力で得られた周辺の単語を確率的に解釈して予測します。
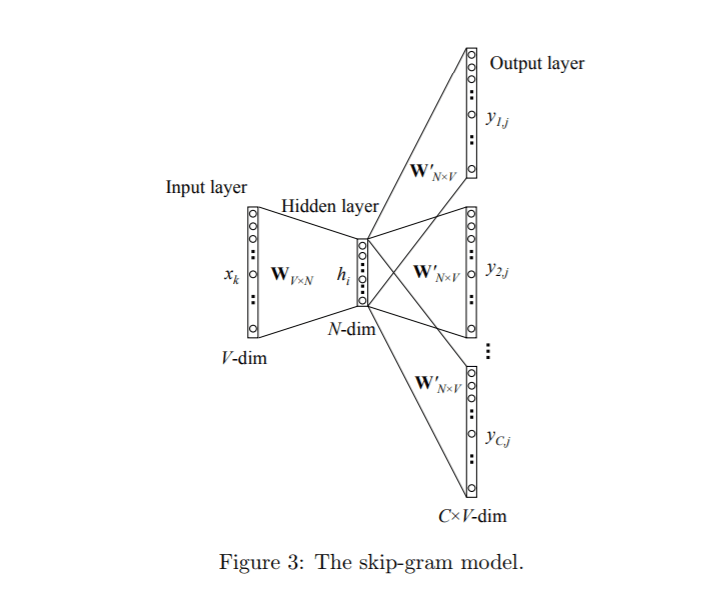
注目しているフレーズ、今回の場合{ I,have,a,pen }をone-hotベクトル化させてFig.3の入力層にいれます。
次に隠れ層で全単語ベクトル{ I,have,a,pen }を並べておき、入力と掛け合わせます。
出力層でも同様に単語ベクトルを並べて行列計算をさせ、最後にsoftmaxを用いて最終的には確率で出力されます。
これをフレーズ{ I,have,a,pen }全体に対して計算させたそれぞれの確率が最大となる重みを探索することで、尤もらしい単語の表現と解釈します。
このようにして単語のベクトル表現を得ることができ、単語の足し算や引き算をすることが可能です。
Fig.4 Skip-gramのアーキテクチャ
word2vec Parameter Learning Explainedより引用
べき乗則
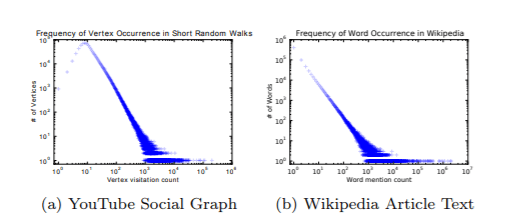
DeepWalkではべき乗則を仮定しています。というのも、自然言語において単語の出現回数はべき乗則に従い、ランダムウォークで選んだノードの数の分布もべき乗則に従います。
そのため、グラフにも自然言語処理と同じアプローチが使えるのではないかと考えて、Skip-gramを用いた解析を行っています。
Fig.5 YouTubeのグラフからランダムウォークさせたときのノードの数とウィキペディア中に現れた単語の数
DeepWalkより引用
DeepWalkの仕組み
DeepWalkは非常にシンプルなアルゴリズムです。ランダムウォークで得られた短い系列データをSkip-gramの入力として扱い、そのノードと関係性が近いノードを予測し、グラフのベクトル表現を得ます。
(注意)名前はDeepWalkですがSkip-gramをそのまま利用しているので、3層のネットワーク(入力層、隠れ層、出力層)のみで構成されています。
再掲
Fig.1にあるように、DeepWalkでKarateネットワークのグラフ構造の特徴を抽出しています。
まとめ
この記事では、DeepWalkを本当に簡単に解説しました。アルゴリズム自体は非常にシンプルであるので、(直感的に)わかりやすいかと思います。
DeepWalkのほかにもアルゴリズムが提案されています。
LINE
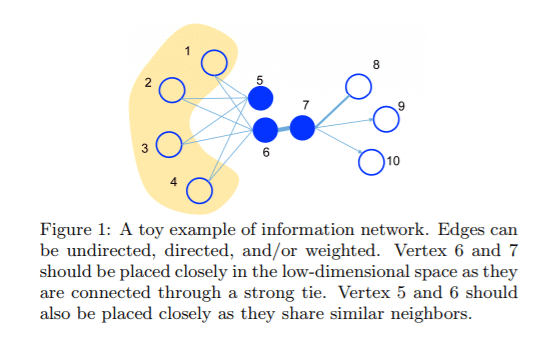
LINE:DeepWalkではノード同士がリンクしているもののみを考慮していますが、LINEではノードが直接リンクしていなくても近しい特徴を有していそうなノードも分散表現を得るときに反映させています。
上の説明だけであるとわかりにくいと思いますので、本家の論文より引用させてもらいました。
下図でいうところのノード5とノード6は直接リンクしていないが、ノード1と4にリンクしているので、近しい特徴を有していそうということも考慮しています。
node2vec
node2vec:基本的にはDeepWalkとアルゴリズムは同じですが、深さ優先探索と幅優先探索によるノードのサンプリングを加えています。