はじめに
深層学習フレームワークPyTorchのチュートリアルの中に「Learning PyTorch with Examples」というページがある。隠れ層がひとつの簡単なネットワーク(多層パーセプトロン)をnumpyだけで実装し、少しずつPyTorchのAPIで置き換えていく内容である。個々のAPIが何をしているのかが直感的に分かるとても良い入門記事となっている。本ブログでは、同じことをChainerで行う。本題に入る前に、ここで取り上げるネットワーク構造を用いて、誤差逆伝播法について手短に説明する。
動作環境
- macOS Sierra
- Python 2.7.14
- Chainer 2.1.0
対象とするネットワークの構造
以下のネットワークを扱う。
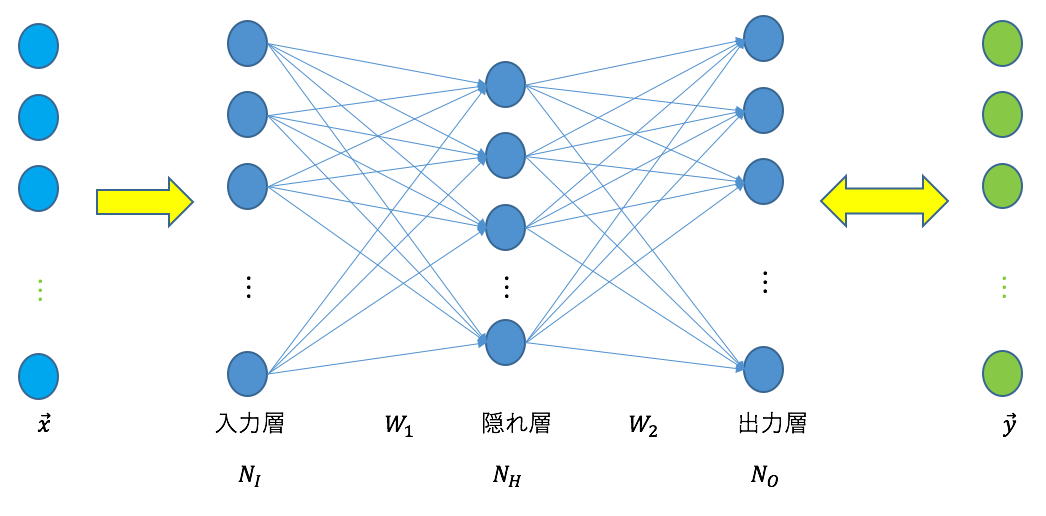
入力層、隠れ層、出力層の3層から成るネットワークである。それぞれのユニット数は、![]() 、
、![]() 、
、![]() である。
である。![]() は入力データ(
は入力データ(![]() 次元の列ベクトル)、
次元の列ベクトル)、![]() はそれに対応する教師データ(
はそれに対応する教師データ(![]() 次元の列ベクトル)を表す。
次元の列ベクトル)を表す。![]() を入力し、その出力を教師データ
を入力し、その出力を教師データ![]() と比較することにより訓練を行う。
と比較することにより訓練を行う。![]() は入力層と隠れ層の間の重みを表す
は入力層と隠れ層の間の重みを表す![]() 行列、
行列、![]() は隠れ層と出力層の間の重みを表す
は隠れ層と出力層の間の重みを表す![]() 行列である。
行列である。
誤差関数
入力データ![]() に対する出力
に対する出力![]() は次式で与えられる。
は次式で与えられる。
(1) 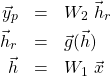
ここで、![]() は次式で定義される活性化関数Rectified Linear Unit(ReLU)である。
は次式で定義される活性化関数Rectified Linear Unit(ReLU)である。
(2) 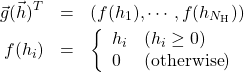
![]() と教師データ
と教師データ![]() を比較するため次の誤差関数を定義する。
を比較するため次の誤差関数を定義する。
(3) ![]()
![]() と
と![]() の各成分の差の2乗和の平均値である。訓練により、
の各成分の差の2乗和の平均値である。訓練により、![]() が最小となるように重み
が最小となるように重み![]() と
と![]() を最適化する。
を最適化する。
誤差逆伝播法と勾配降下法
![]() を
を![]() と
と![]() で偏微分する。
で偏微分する。![]() の成分を
の成分を![]() 、
、![]() の成分を
の成分を![]() と書くことにする。微分の連鎖律を用いて、
と書くことにする。微分の連鎖律を用いて、
(4) 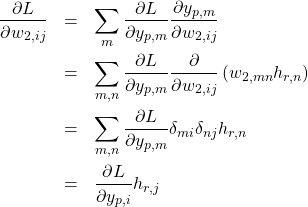
(5) 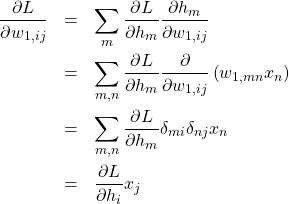
を得る。式(5)の最後の式に現れる![]() は以下のように変形できる。
は以下のように変形できる。
(6) 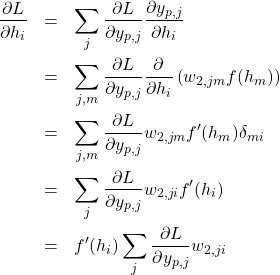
すなわち、![]() は式(4)の最後の式に現れる
は式(4)の最後の式に現れる![]() を使って計算することができる。
を使って計算することができる。![]() は、最上層(出力層)の出力
は、最上層(出力層)の出力![]() についての微分であり、これさえ計算できれば最下層(入力層)の出力
についての微分であり、これさえ計算できれば最下層(入力層)の出力![]() についての微分
についての微分![]() を求めることができる。いま、
を求めることができる。いま、
(7) ![]()
である。これはネットワークの出力と教師データの差分、すなわち、誤差を表す。誤差を下層に向かって伝播することになる(誤差逆伝播法)。式(7)を用いて、
(8) 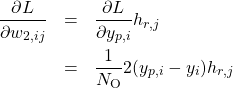
を得る。行列の形で書けば
(9) ![]()
となる。ここで、![]() は転置を表す。同様にして、
は転置を表す。同様にして、
(10) 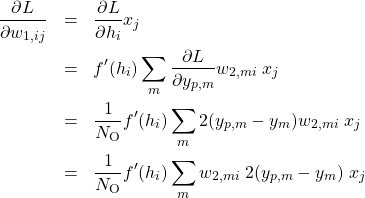
を得る。ただし、![]() は
は![]() のとき
のとき![]() 、それ以外のときは
、それ以外のときは![]() となることに注意する。行列の形で書けば、
となることに注意する。行列の形で書けば、
(11) ![]()
である。ただし、![]() のときは
のときは![]() であることに注意する。これらを用いて、
であることに注意する。これらを用いて、![]() と
と![]() を以下のように更新する。
を以下のように更新する。
(12) 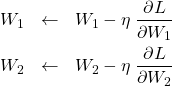
ここで、![]() は学習率(正の微小量)である。上の更新を繰り返すことにより、
は学習率(正の微小量)である。上の更新を繰り返すことにより、![]() を最小値に近づけていく(勾配降下法)。
を最小値に近づけていく(勾配降下法)。
上の議論は1つのデータの組み![]() に対するものである。
に対するものである。![]() 個の組みを扱う場合、式(9),(11)は以下のように拡張される。
個の組みを扱う場合、式(9),(11)は以下のように拡張される。
(13) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{\partial L}{\partial W_2}&=&\frac{1}{N_{\rm O}}2(Y_p-Y)\;H_r^T \\ \frac{\partial L}{\partial W_1}&=&\frac{1}{N_{\rm O}}\left[W_2^T\;2(Y_p-Y)\right]\;X^T \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-2a0a2f44020f66d5226c32f704a7ac33_l3.png)
ここで、新たに以下の行列を導入した。
(14) 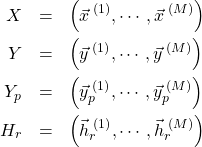
実際のコードでは、計算効率のため、ここまでに定義した全ての行列の行と列を転置したものを扱う。後で示すコードと一致させるため、式(13)をさらに変形しておく。式(13)の両辺の転置を取って、
(15) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left(\frac{\partial L}{\partial W_2}\right)^T &=&\left(\frac{1}{N_{\rm O}}2(Y_p-Y)\;H_r^T\right)^T \\ &=&\frac{1}{N_{\rm O}}H_r\;2(Y_p-Y)^T \\ \left(\frac{\partial L}{\partial W_1}\right)^T &=&\left(\frac{1}{N_{\rm O}}\left[W_2^T\;2(Y_p-Y)\right]\;X^T\right)^T \\ &=&\frac{1}{N_{\rm O}}X \left[2(Y_p-Y)^T\;W_2\right] \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-de8a82fc09e719ef195f8e26deecebaf_l3.png)
行と列を入れ替えた行列を同じ表記のまま改めて定義し直すと次式を得る。
(16) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{\partial L}{\partial W_2} &=&\frac{1}{N_{\rm O}}H_r^T\;2(Y_p-Y) \\ \frac{\partial L}{\partial W_1} &=&\frac{1}{N_{\rm O}}X^T\left[2(Y_p-Y)\;W_2^T\right] \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-d8c7fb0ef5d43e281fd6dc214c111870_l3.png)
numpyによる実装
最初にChainerを使わずnumpyだけを用いて実装したものを示す(PyTorchの記事と同じ)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np EPOCHS = 300 M = 64 N_I = 1000 N_H = 100 N_O = 10 LEARNING_RATE = 1.0e-04 # set a specified seed to random value generator in order to reproduce the same results np.random.seed(1) X = np.random.randn(M, N_I).astype(np.float32) Y = np.random.randn(M, N_O).astype(np.float32) W1 = np.random.randn(N_I, N_H).astype(np.float32) W2 = np.random.randn(N_H, N_O).astype(np.float32) def sample_1(): # create random input and output data x = X y = Y # randomly initialize weights w1 = W1 w2 = W2 y_size = np.float32(M * N_O) for t in range(EPOCHS): # forward pass h = x.dot(w1) h_r = np.maximum(h, 0) y_p = h_r.dot(w2) # compute mean squared error and print loss loss = np.square(y_p - y).sum() / y_size print(loss) # backward pass: compute gradients of loss with respect to w2 grad_y_p = 2.0 * (y_p - y) / y_size grad_w2 = h_r.T.dot(grad_y_p) # backward pass: compute gradients of loss with respect to w1 grad_h_r = grad_y_p.dot(w2.T) grad_h = grad_h_r grad_h[h < 0] = 0 grad_w1 = x.T.dot(grad_h) # update weights w1 -= LEARNING_RATE * grad_w1 w2 -= LEARNING_RATE * grad_w2 if __name__ == '__main__': sample_1() |
- 24-25行目:
 と
と に適当な値を設定する。
に適当な値を設定する。 - 28-29行目:
 と
と を適当な値で初期化する。
を適当な値で初期化する。 - 32行目以降:勾配降下法を行うルーチンである。
- 34-36行目:
 を計算する(forward計算)。
を計算する(forward計算)。 - 39行目:
 を計算する。
を計算する。 - 43-44行目:
 を計算する(backward計算)。
を計算する(backward計算)。 - 47-50行目:
 を計算する(backward計算)。
を計算する(backward計算)。 - 53-54行目:
 と
と を更新する。
を更新する。
理論式と一対一対応していることに注意する。
chainer.Variableの導入
上のコードでは微分計算を全て書き下ろした。chainer.Variableを使うことで、微分計算を自動化することができる。書き換えの手順は以下の通りである。
- numpy.arrayからVariable変数を作る(26,27,30,31行目)。
- numpy.array間の演算を行う関数をchainer.functions内の関数に置き換える(35,36,37,40行目)。
- lossを求めた(35-40行目)あと、loss.backwardを実行する(49行目)。ここで誤差逆伝播法が実行される。
- 微分値は、w1.gradとw2.gradで得ることができる(52-53行目)。
- 適当なタイミングでw1とw2の勾配のゼロ初期化が必要である(44-45行目)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import chainer.functions as F from chainer import Variable EPOCHS = 300 M = 64 N_I = 1000 N_H = 100 N_O = 10 LEARNING_RATE = 1.0e-04 # set a specified seed to random value generator in order to reproduce the same results np.random.seed(1) X = np.random.randn(M, N_I).astype(np.float32) Y = np.random.randn(M, N_O).astype(np.float32) W1 = np.random.randn(N_I, N_H).astype(np.float32) W2 = np.random.randn(N_H, N_O).astype(np.float32) def sample_2(): # create random input and output data x = Variable(X) y = Variable(Y) # randomly initialize weights w1 = Variable(W1) w2 = Variable(W2) for t in range(EPOCHS): # forward pass: compute predicted y h = F.matmul(x, w1) h_r = F.relu(h) y_p = F.matmul(h_r, w2) # compute and print loss loss = F.mean_squared_error(y_p, y) print(loss.data) # manually zero the gradients w1.zerograd() w2.zerograd() # backward pass # loss.grad = np.ones(loss.shape, dtype=np.float32) loss.backward() # update weights w1.data -= LEARNING_RATE * w1.grad w2.data -= LEARNING_RATE * w2.grad if __name__ == '__main__': sample_2() |
Variableとchainer.functionsを使うことで、背後で自動微分が実行される。
chainer.Chainの導入
オリジナルなネットワークを、chainer.Chainを継承したクラスとして実装することができる。forward計算をメソッド__call__内で定義する(34-38行目)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import chainer from chainer import Variable import chainer.functions as F import chainer.links as L EPOCHS = 300 M = 64 N_I = 1000 N_H = 100 N_O = 10 LEARNING_RATE = 1.0e-04 # set a specified seed to random value generator in order to reproduce the same results np.random.seed(1) X = np.random.randn(M, N_I).astype(np.float32) Y = np.random.randn(M, N_O).astype(np.float32) W1 = np.random.randn(N_I, N_H).astype(np.float32) W2 = np.random.randn(N_H, N_O).astype(np.float32) class TwoLayerNet(chainer.Chain): def __init__(self, d_in, h, d_out): super(TwoLayerNet, self).__init__( linear1=L.Linear(d_in, h, initialW=W1.transpose()), linear2=L.Linear(h, d_out, initialW=W2.transpose()) ) def __call__(self, x): g = self.linear1(x) h_r = F.relu(g) y_p = self.linear2(h_r) return y_p def sample_3(): # create random input and output data x = Variable(X) y = Variable(Y) # create a network model = TwoLayerNet(N_I, N_H, N_O) for t in range(EPOCHS): # forward y_p = model(x) # compute and print loss loss = F.mean_squared_error(y_p, y) print(loss.data) # zero the gradients model.cleargrads() # backward loss.backward() # update weights model.linear1.W.data -= LEARNING_RATE * model.linear1.W.grad model.linear2.W.data -= LEARNING_RATE * model.linear2.W.grad if __name__ == '__main__': sample_3() |
chainer.optimizerの導入
ここまでの例では重みの更新式を露わに書いてきた。chainer.optimizersを使うことで、この煩雑さをなくすことできる(71行目)。 今回の最適化手法は(確率的)勾配降下法であるが(51行目)、chainer.optimizersは様々な最適化手法を提供している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import chainer from chainer import Variable import chainer.functions as F import chainer.optimizers as P import chainer.links as L EPOCHS = 300 M = 64 N_I = 1000 N_H = 100 N_O = 10 LEARNING_RATE = 1.0e-04 # set a specified seed to random value generator in order to reproduce the same results np.random.seed(1) X = np.random.randn(M, N_I).astype(np.float32) Y = np.random.randn(M, N_O).astype(np.float32) W1 = np.random.randn(N_I, N_H).astype(np.float32) W2 = np.random.randn(N_H, N_O).astype(np.float32) class TwoLayerNet(chainer.Chain): def __init__(self, d_in, h, d_out): super(TwoLayerNet, self).__init__( linear1=L.Linear(d_in, h, initialW=W1.transpose()), linear2=L.Linear(h, d_out, initialW=W2.transpose()) ) def __call__(self, x): g = self.linear1(x) h_r = F.relu(g) y_p = self.linear2(h_r) return y_p def sample_4(): # create random input and output data x = Variable(X) y = Variable(Y) # create a network model = TwoLayerNet(N_I, N_H, N_O) # create an optimizer optimizer = P.SGD(lr=LEARNING_RATE) # connect the optimizer with the network optimizer.setup(model) for t in range(EPOCHS): # forward pass: compute predicted y y_p = model(x) # compute and print loss loss = F.mean_squared_error(y_p, y) print(loss.data) # zero the gradients model.cleargrads() # backward loss.backward() # update weights optimizer.update() if __name__ == '__main__': sample_4() |
ここまでの置き換えで、ループの中の処理をかなりクリアにするこができた。
chainer.trainingの導入
ここまでの例では、勾配降下法を行うループを露わに書いてきた。chainer.trainingなどを使うことでループをなくすことができる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import chainer import chainer.functions as F import chainer.optimizers as P import chainer.links as L import chainer.datasets as D import chainer.iterators as Iter from chainer import training from chainer.training import extensions from chainer import reporter EPOCHS = 300 M = 64 N_I = 1000 N_H = 100 N_O = 10 LEARNING_RATE = 1.0e-04 # set a specified seed to random value generator in order to reproduce the same results np.random.seed(1) X = np.random.randn(M, N_I).astype(np.float32) Y = np.random.randn(M, N_O).astype(np.float32) W1 = np.random.randn(N_I, N_H).astype(np.float32) W2 = np.random.randn(N_H, N_O).astype(np.float32) class TwoLayerNet(chainer.Chain): def __init__(self, d_in, h, d_out): super(TwoLayerNet, self).__init__( linear1=L.Linear(d_in, h, initialW=W1.transpose()), linear2=L.Linear(h, d_out, initialW=W2.transpose()) ) def __call__(self, x): g = self.linear1(x) h_r = F.relu(g) y_p = self.linear2(h_r) return y_p class LossCalculator(chainer.Chain): def __init__(self, model): super(LossCalculator, self).__init__() with self.init_scope(): self.model = model def __call__(self, x, y): y_p = self.model(x) loss = F.mean_squared_error(y_p, y) reporter.report({'loss': loss}, self) return loss def sample_5(): # make a iterator dataset = D.TupleDataset(X, Y) train_iter = Iter.SerialIterator(dataset, batch_size=M, shuffle=False) # create a network model = TwoLayerNet(N_I, N_H, N_O) loss_calculator = LossCalculator(model) # create an optimizer optimizer = P.SGD(lr=LEARNING_RATE) # connect the optimizer with the network optimizer.setup(loss_calculator) # make a updater updater = training.StandardUpdater(train_iter, optimizer) # make a trainer trainer = training.Trainer(updater, (EPOCHS, 'epoch'), out='result') trainer.extend(extensions.LogReport()) trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'elapsed_time'])) trainer.run() if __name__ == '__main__': sample_5() |
上のコードは、numpyによるコードと異なり、何をするのかを宣言するコードとなっている。これが、Chainerによる抽象化の恩恵である。もちろん、これら5つのスクリプトで計算した誤差(loss)とエポック(epoch)の関係は(ほぼ)一致する。
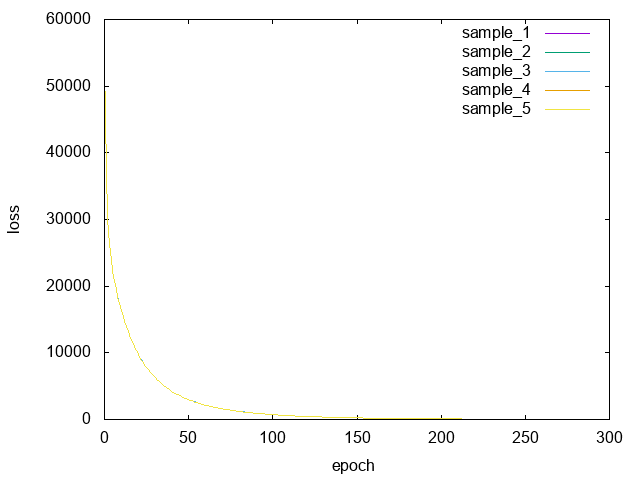
epoch数が増えるにつれて誤差は小さくなることが分かる。
まとめ
Chainerの提供するAPIを使うことにより、深層学習の背後にある煩雑さ(誤差逆伝播法、勾配降下法をはじめとする各種最適化手法などの詳細)を隠蔽して、ネットワーク構造やその訓練過程を実装することができる。今回は触れなかったが、数行追加するだけでGPUとCPUのどちらでも動作するコードに仕立て上げることも可能である。
これまでに大変多くの深層学習フレームワークが公開されている。どれか一つに固執することなく複数のフレームワークを使うことをお薦めしたい。各フレームワークの長所・短所を知ることで深層学習についての理解も深まるためである。

