はじめに
先の投稿でBayes推定に触れた。今回は、回帰問題を例に取り、最尤推定・MAP推定・Bayes推定を統一的に解説したい。
尤度・事後分布・事前分布
最初に先の解説の一部を再掲載する。
いま、![]() が観測されているとする。
が観測されているとする。![]() が説明変数、
が説明変数、![]() が目的変数である。このとき、潜在変数
が目的変数である。このとき、潜在変数![]() を導入し、同時確率分布
を導入し、同時確率分布![]() を考える。この分布にBayesの定理を適用すると次式を得る。
を考える。この分布にBayesの定理を適用すると次式を得る。
(1) ![]()
ただし、式変形の途中で、![]() を用いた。式(1)の左辺にある
を用いた。式(1)の左辺にある![]() を事後分布、右辺の分子にある
を事後分布、右辺の分子にある![]() を尤度、
を尤度、![]() を事前分布、右辺分母にある
を事前分布、右辺分母にある![]() をモデルエビデンスと呼ぶ。いま、事後分布の
をモデルエビデンスと呼ぶ。いま、事後分布の![]() 依存性に注目すると、式(1)の右辺分母は定数と見なすことができる。したがって
依存性に注目すると、式(1)の右辺分母は定数と見なすことができる。したがって
(2) ![]()
と書くことができる。尤度と事前分布に、![]() をパラメータとして持つ適当な関数を仮定し回帰問題を解くことになる。
をパラメータとして持つ適当な関数を仮定し回帰問題を解くことになる。
最尤推定
最尤推定では式(2)の右辺にある尤度![]() を潜在変数
を潜在変数![]() について最大化することにより回帰問題を解く。事前分布は考慮しない。観測値が独立同分布から得られていると仮定すると、尤度は以下のように変形できる。
について最大化することにより回帰問題を解く。事前分布は考慮しない。観測値が独立同分布から得られていると仮定すると、尤度は以下のように変形できる。
(3) 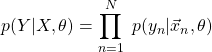
(4) ![]()
ここで、![]() 次元ベクトル
次元ベクトル![]() と
と![]() がパラメータ
がパラメータ![]() に相当する。
に相当する。![]() は分散の逆数であり、精度(precision)と呼ばれる量である。式(3)の対数をとり、式(4)を代入すると次式を得る。
は分散の逆数であり、精度(precision)と呼ばれる量である。式(3)の対数をとり、式(4)を代入すると次式を得る。
(5) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \ln{p(Y|X,\theta)}&=&\sum_{n=1}^N\ln{\left\{\left(\frac{1}{2\pi}\right)^{1/2}\lambda^{1/2}\exp{\left[-\frac{\lambda}{2}\left(y_n-\vec{w}^{\;T}\vec{x}_n\right)^2\right]}\right\}}\\ &=&-\frac{N}{2}\ln{2\pi}+\frac{N}{2}\ln{\lambda}-\frac{\lambda}{2}\sum_{n=1}^{N}(y_n-\vec{w}^{\;T}\vec{x}_n)^2 \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-80d657242f500c805cc7e4e358615144_l3.png)
式(5)を![]() で微分した式を0とおけば、最尤推定による
で微分した式を0とおけば、最尤推定による![]() (
(![]() と書くことにする)が決定される。
と書くことにする)が決定される。
(6) ![]()
ここで、![]() は
は![]() の行列であり、その成分は
の行列であり、その成分は![]() で定義される。
で定義される。![]() はベクトル
はベクトル![]() の第
の第![]() 成分である。また、
成分である。また、![]() とした。同様に、
とした。同様に、![]() で微分した式を0とおけば、
で微分した式を0とおけば、![]() が求まる。
が求まる。
(7) 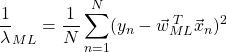
未知変数![]() が与えられた時、最尤推定が予測する目的変数の値
が与えられた時、最尤推定が予測する目的変数の値![]() は次式で求められる。
は次式で求められる。
(8) ![]()
その分散は
(9) ![]()
である。分散は定数であり、未知変数![]() に依存しない。最尤推定ではパラメータ
に依存しない。最尤推定ではパラメータ![]() の取り得る範囲に制限を与えず最適な値を探索する。これが過学習をもたらす原因である。
の取り得る範囲に制限を与えず最適な値を探索する。これが過学習をもたらす原因である。![]() の取り得る範囲に制限を付加したものが次に示すMAP推定である。
の取り得る範囲に制限を付加したものが次に示すMAP推定である。
MAP推定
MAP推定では事前分布![]() を考慮することで、
を考慮することで、![]() の取り得る範囲に制限を与える。
の取り得る範囲に制限を与える。
(10) 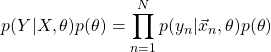
この式を最大化することで回帰問題を解く。![]() として先と同じ正規分布を仮定し、
として先と同じ正規分布を仮定し、![]() として次の正規分布を仮定する。
として次の正規分布を仮定する。
(11) ![]()
ここで、![]() は
は![]() 次元ベクトル、
次元ベクトル、![]() は
は![]() 行列である。ともにあらかじめ決めておく量である。
行列である。ともにあらかじめ決めておく量である。![]() は最尤推定と同じく計算により求める量であることに注意する。式(10)に式(4)と式(11)を代入し、対数を取る。
は最尤推定と同じく計算により求める量であることに注意する。式(10)に式(4)と式(11)を代入し、対数を取る。
(12) 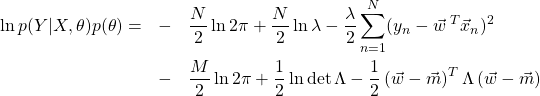
この式を![]() で微分した式を0とおくと、MAP推定による
で微分した式を0とおくと、MAP推定による![]() (
(![]() と書くことにする)を得る。
と書くことにする)を得る。
(13) ![]()
![]() で微分すると次式を得る。
で微分すると次式を得る。
(14) 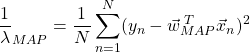
いま簡単のため、![]() とする。すなわち、
とする。すなわち、![]() は正規分布
は正規分布![]() から生成されると仮定する。このとき
から生成されると仮定する。このとき
(15) 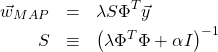
となる。未知変数![]() が与えられた時、MAP推定が予測する目的変数の値
が与えられた時、MAP推定が予測する目的変数の値![]() は次式で求められる。
は次式で求められる。
(16) ![]()
その分散は
(17) ![]()
である。分散は定数であり、未知変数![]() に依存しない。
に依存しない。
最尤推定・MAP推定の実験
最尤推定とMAP推定を用いて、具体的に回帰問題を解いてみる。考える正解曲線![]() を次式で定義する。
を次式で定義する。
(18) ![]()
適当に10(=![]() )個の点をサンプルしこれを観測点とする。観測点を生成する際に、以下のようにノイズを付加した。
)個の点をサンプルしこれを観測点とする。観測点を生成する際に、以下のようにノイズを付加した。
(19) ![]()
![]() =0.015とした。また、
=0.015とした。また、![]() とおく。すなわち、
とおく。すなわち、![]() 次式で曲線を再現することを考える。最初に最尤推定の結果を示す。
次式で曲線を再現することを考える。最初に最尤推定の結果を示す。
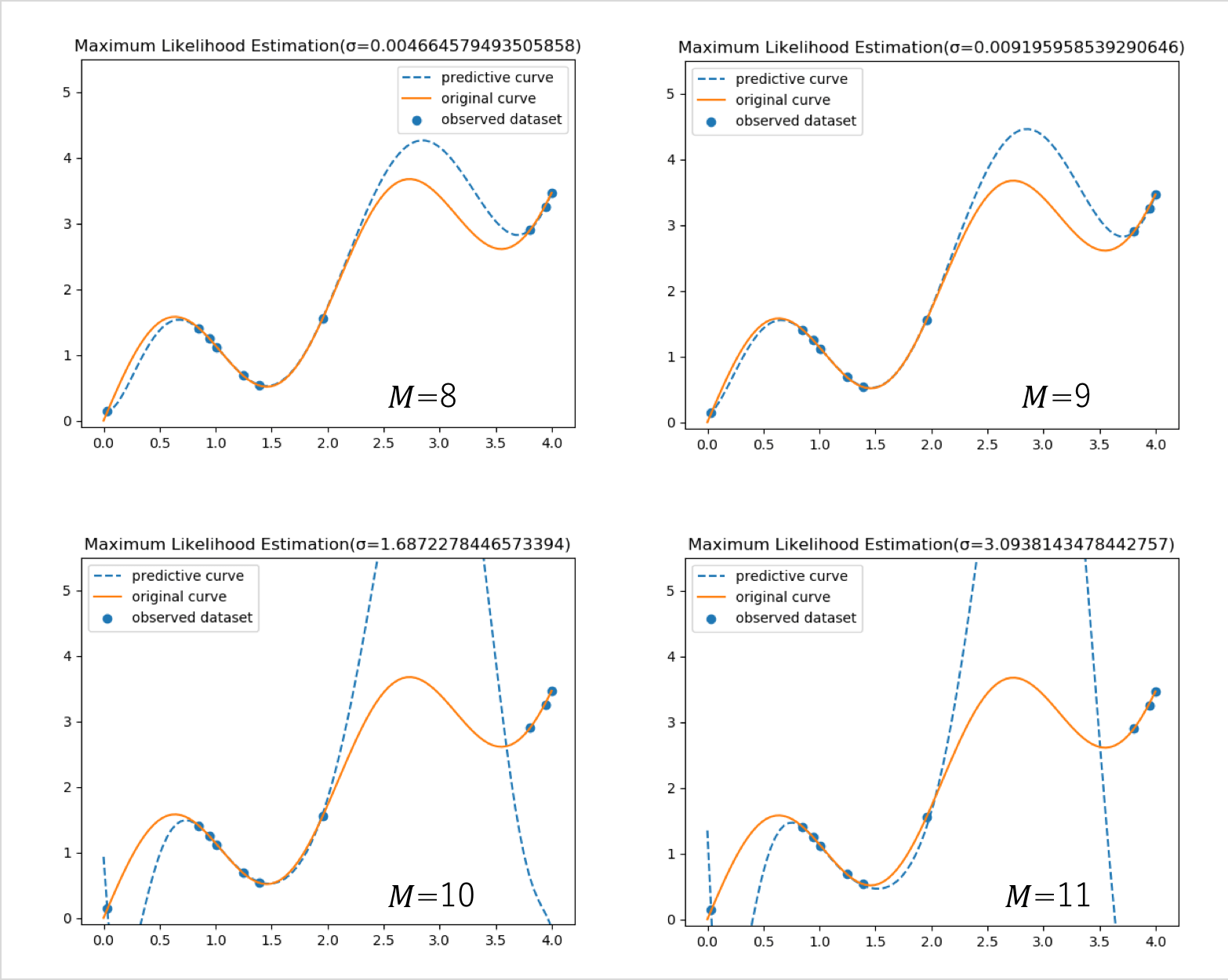
次に、MAP推定の結果を示す。![]() とした。
とした。
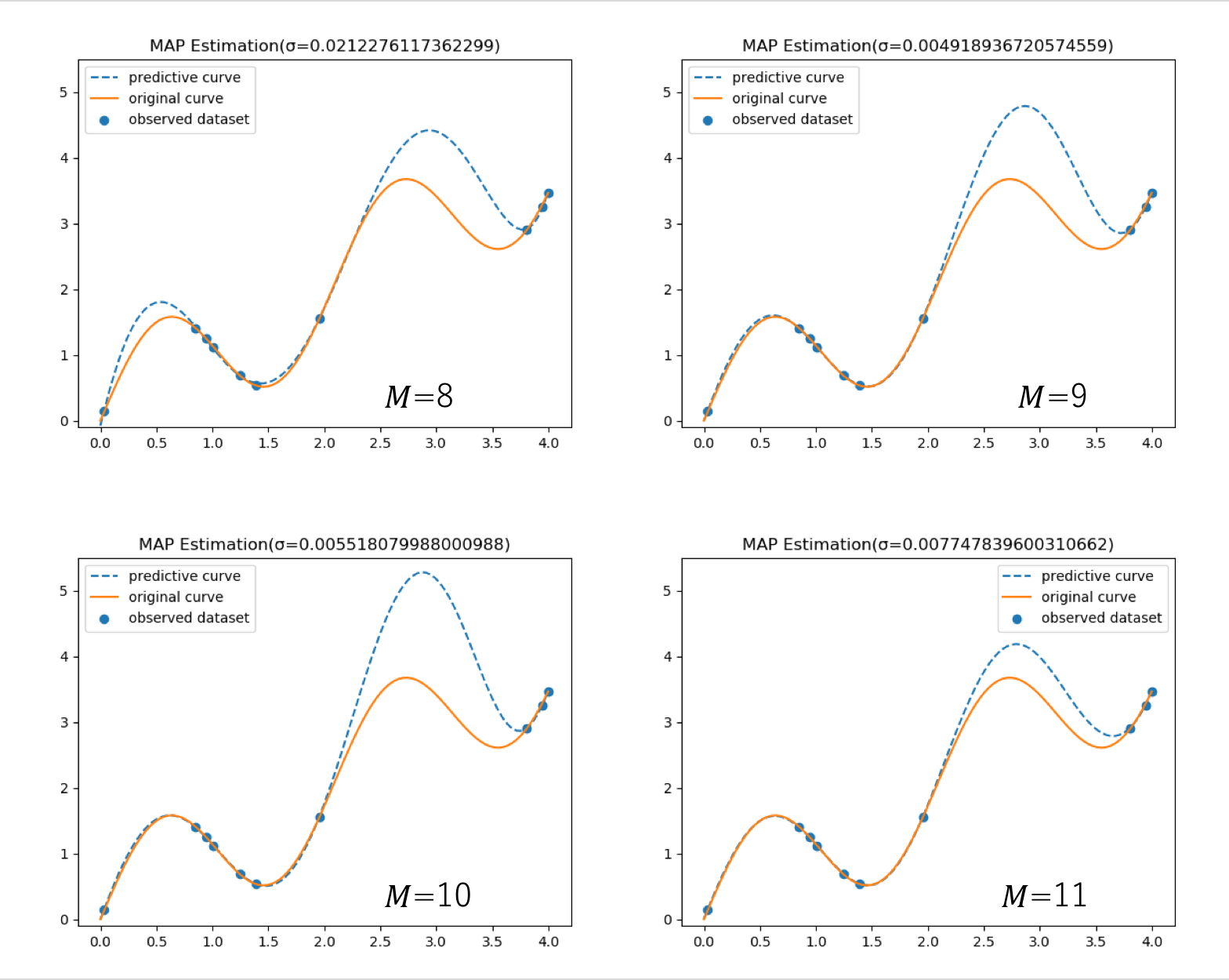
![]() を大きくしていくと、最尤推定の方は、左側にある観測点で過学習となり始め、右側の観測点を再現できなくなる。一方、MAP推定の方はどの次元においても観測点近傍を通る曲線を再現できている。各図のタイトルの横に標準偏差を示した。最尤推定・MAP推定から求まる分散は
を大きくしていくと、最尤推定の方は、左側にある観測点で過学習となり始め、右側の観測点を再現できなくなる。一方、MAP推定の方はどの次元においても観測点近傍を通る曲線を再現できている。各図のタイトルの横に標準偏差を示した。最尤推定・MAP推定から求まる分散は![]() に依存しない定数なので、各予測点の確からしさを表す量ではない。最尤推定とMAP推定は、「点」を予測する手法であり、点推定(Point Estimation)と総称される。
に依存しない定数なので、各予測点の確からしさを表す量ではない。最尤推定とMAP推定は、「点」を予測する手法であり、点推定(Point Estimation)と総称される。
Bayes推定
再度、式(1)に戻って議論を行う。
(20) ![]()
(21) ![]()
事後分布![]() を求めることができれば、次式により未知変数
を求めることができれば、次式により未知変数![]() に対する予測値
に対する予測値![]() を計算することができる。
を計算することができる。
(22) ![]()
Bayes推定の目的は、事後分布![]() を求めることである。
を求めることである。
尤度と事前分布として、最尤推定・MAP推定のときと同じ正規分布を仮定する。尤度に対しては式(4)を、事前分布に対しては式(11)を用いる。ここで、注意しなければならないことがある。MAP推定では天下り的に事前分布として![]() に対する確率分布だけを与えたが、Bayes推定では、厳密に以下の場合を考える必要がある。
に対する確率分布だけを与えたが、Bayes推定では、厳密に以下の場合を考える必要がある。
 を固定し、
を固定し、 を推定したい場合
を推定したい場合 を固定し、
を固定し、 を推定したい場合
を推定したい場合- 両方とも推定したい場合
それぞれに対し、任意の確率分布を仮定することができるが、次のようにおくことにより事後分布を解析的に扱いやすい形にすることができる。
このように事後分布を同じ関数形にできる事前分布を共役事前分布と呼ぶ。ここでは、1を採用したことになる。すなわち、![]() についてはあらかじめ決めておく定数とする。
についてはあらかじめ決めておく定数とする。
さて、これらを式(20)の右辺分子に代入する。分母の計算には式(21)を用いる。ガウス関数なので積分は容易に実行できる。最終的に事後分布も正規分布となる。
(23) ![]()
ここで、
(24) 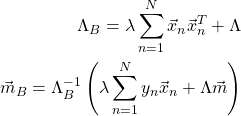
とした。さらに、式(22)も解析的に計算することができる。
(25) ![]()
ただし、
(26) ![]()
とおいた。MAP推定のときと同じ仮定
(27) ![]()
をおくと
(28) 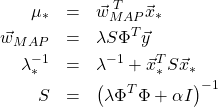
を得る。MAP推定のときに求めた![]() (式(15))が現れることに注意する。Bayes推定では、式(25)の正規分布が求めるべき解となる。すなわち、回帰曲線を「点」ではなく確率として求める点が最尤推定やMAP推定との大きな違いである。また、
(式(15))が現れることに注意する。Bayes推定では、式(25)の正規分布が求めるべき解となる。すなわち、回帰曲線を「点」ではなく確率として求める点が最尤推定やMAP推定との大きな違いである。また、![]() はあらかじめ決めておく量であることに注意する。
はあらかじめ決めておく量であることに注意する。
先と同じ問題に適用した結果を以下に示す。今の場合、正解曲線からサンプルする際のノイズ分布は既知(平均0、標準偏差![]() の正規分布)であるから、
の正規分布)であるから、![]() とすることができるが、現実の問題に適応する際は、観測データについての何らかの事前知識が必要になる。
とすることができるが、現実の問題に適応する際は、観測データについての何らかの事前知識が必要になる。![]() についてはMAP推定のときと同じ値(0.1)を用いた。
についてはMAP推定のときと同じ値(0.1)を用いた。
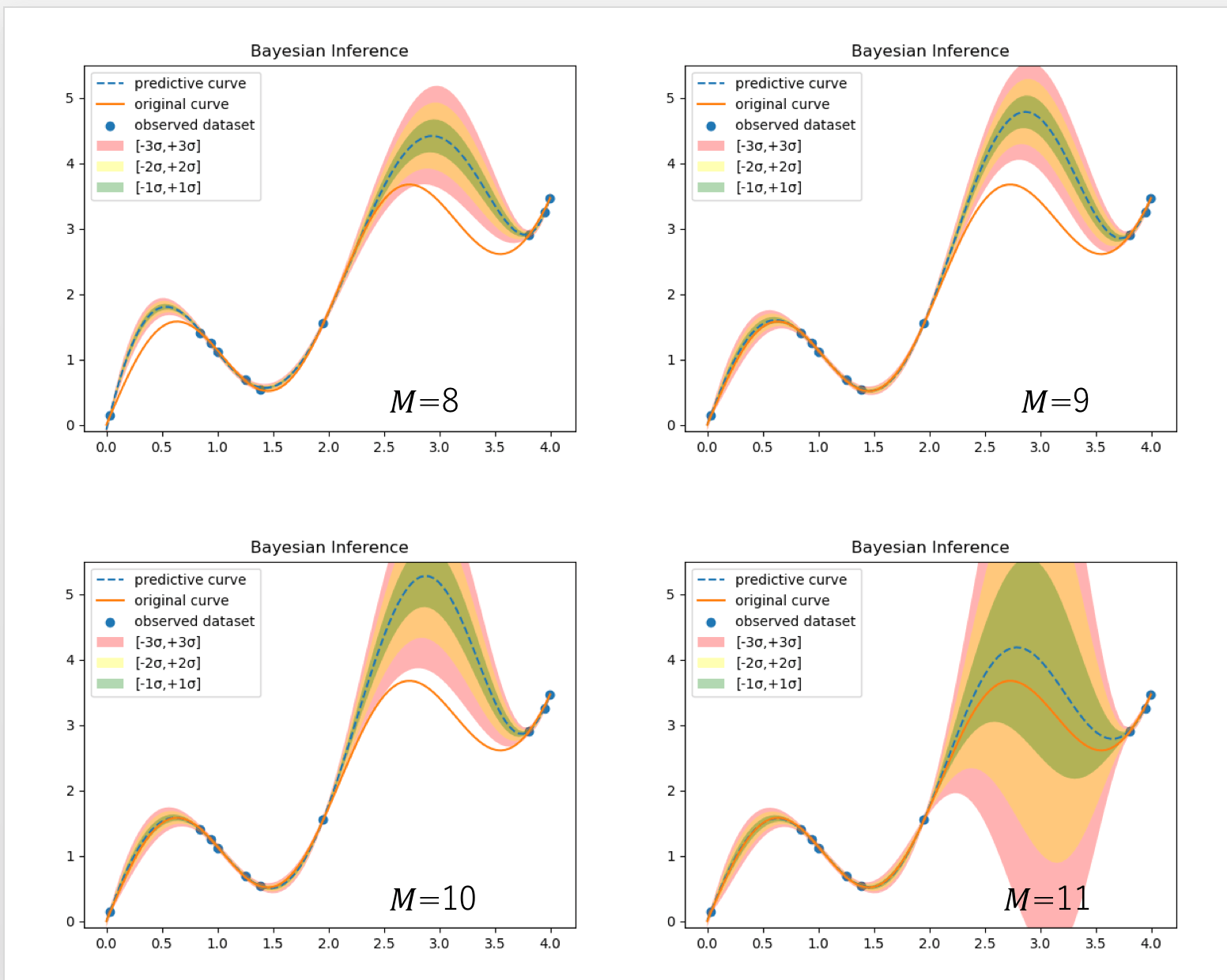
図の点線は正規分布(式(25))の平均値をプロットしたものである。色ぬりした領域は標準偏差である。最尤推定やMAP推定との大きな違いは標準偏差が各点ごとに計算されることである。これがBayes推定から求まる予測値の不確かさ(uncertainty)に相当する。不確かさは、観測値が密にある領域では小さく、疎である領域では大きくなることが分かる。
まとめ
今回は、最尤推定、MAP推定、Bayes推定に対する統一的な解説を試みた。最尤推定は尤度を最大化するパラメータを無制限に探索する。MAP推定では事前分布を導入し、パラメータの探索範囲を制限することにより、過学習を抑制する。これら2つの手法は点推定と呼ばれ、予測値の不確かさを求めることはできない。一方、Bayes推定では、点ではなく確率(事後分布)を求めることが目的となる。確率を求めるのであるから、予測値の不確かさを自然に表現することができる。
コードの場所
今回のコードはここにある。pythonではなくてjuliaで実装した。

