はじめに
今回は、翻訳モデルであるEncoder-Decoderの中で使われるAttentionメカニズムについて解説したい。LSTMなどの詳細についてここでは言及しない。
Encoder-Decoderモデル
Encoder-Decoderモデルとは、入力系列を出力系列に変換するモデルである。その構造を以下に示す。
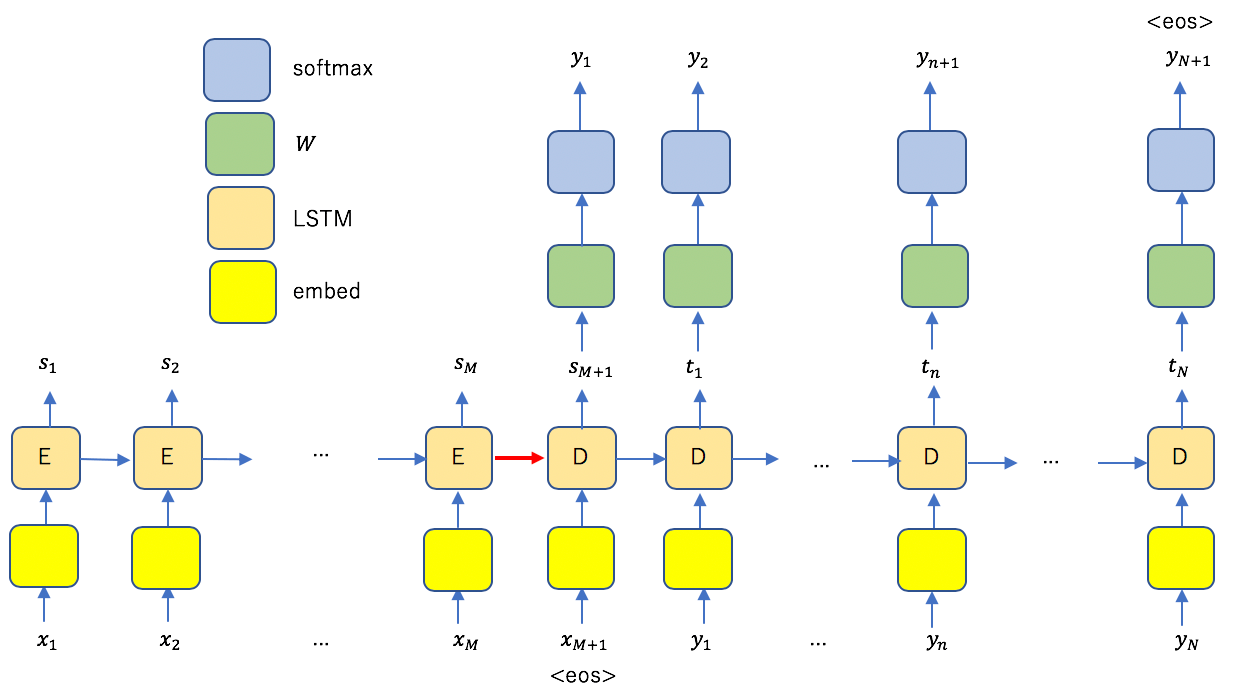
入力系列を![]() 、出力系列を
、出力系列を![]() とした。それぞれの末尾に系列の終了を表すeosを追加してある。橙色の矩形がLSTMを表し、EncoderとDecoderの役割を果たしている。EncoderとDecoderは図の赤矢印のみで接続しており、Encoder側の情報は全てこの矢印一本に集約していることになる。
とした。それぞれの末尾に系列の終了を表すeosを追加してある。橙色の矩形がLSTMを表し、EncoderとDecoderの役割を果たしている。EncoderとDecoderは図の赤矢印のみで接続しており、Encoder側の情報は全てこの矢印一本に集約していることになる。
Attentionメカニズム
出力系列のひとつを予測する際、入力系列の各要素に重み付けを行い、これらも予測に利用する仕組みがAttentionである。
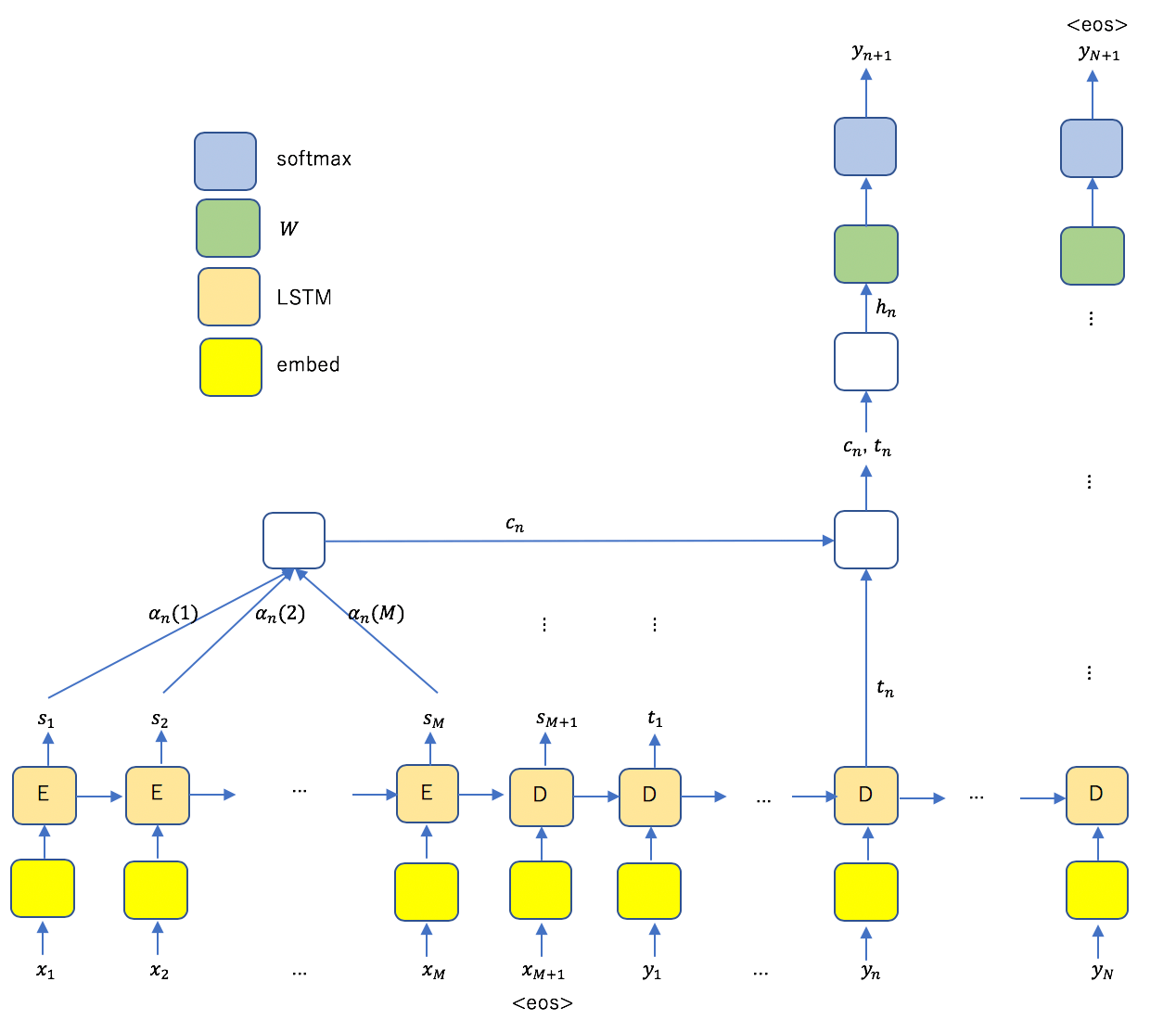
ここで
(1) 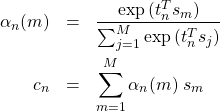
である。上図内の![]() が予測に利用されるメカニズムがAttentionである。
が予測に利用されるメカニズムがAttentionである。![]() はベクトル(
はベクトル(![]() )なので、指数関数の肩に乗る量は内積であることに注意する(
)なので、指数関数の肩に乗る量は内積であることに注意する(![]() は転置を表す)。この式の意味を明確にするため、式(1)を行列で表示する。
は転置を表す)。この式の意味を明確にするため、式(1)を行列で表示する。![]() とし、さらに
とし、さらに![]() と書くことにすれば
と書くことにすれば
(2) ![]()
と書くことができる。図で示すと以下のようになる。
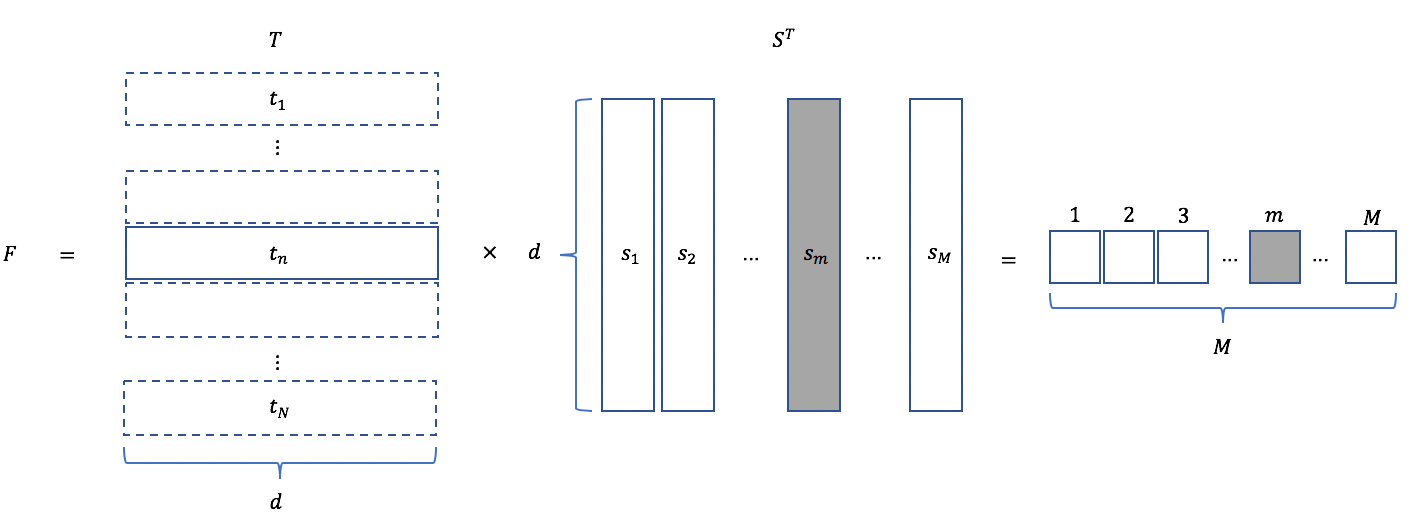
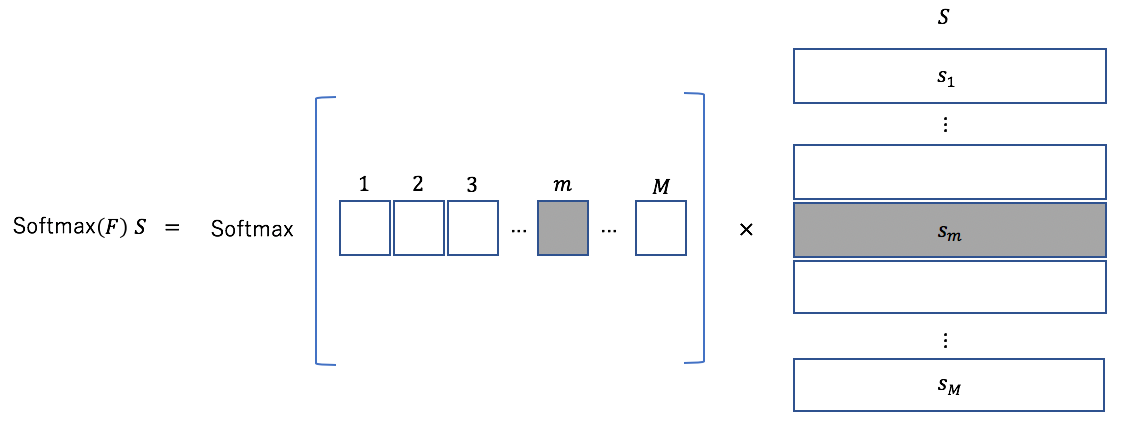
例えば、Decoder側の要素![]() に注目する。このベクトルとEncoder側のベクトル
に注目する。このベクトルとEncoder側のベクトル![]() とが個々に内積を取ることになり、出力は図に示したように
とが個々に内積を取ることになり、出力は図に示したように![]() 次元のベクトルになる。
次元のベクトルになる。![]() との相関が強ければ
との相関が強ければ![]() 番目の要素が大きくなる。これにSoftmaxを施して
番目の要素が大きくなる。これにSoftmaxを施して![]() とかけ算を行えば、入力側の要素のうち、
とかけ算を行えば、入力側の要素のうち、![]() との相関が強い要素
との相関が強い要素![]() にかかる重みが大きくなる。つまり、Attentionとは、出力系列の要素と強く相関する入力系列の要素を抽出する仕組みである。
にかかる重みが大きくなる。つまり、Attentionとは、出力系列の要素と強く相関する入力系列の要素を抽出する仕組みである。
まとめ
今回はAttentionの意味を明確に示した。Attentionは最近の深層学習の研究においてかなり重要なメカニズムとなっている。

