はじめに
今回は、Automatic Relevance Determination(ARD)について解説する。ARDとは、目的変数に対する個々の説明変数の寄与の大きさを見積もる手法である。今回は以下の2つの文脈でARDを行う。
ベイズ推定を用いた回帰によるARD
定式化
目的変数を![]() 、説明変数を
、説明変数を![]() とする。ここで、
とする。ここで、![]() である。潜在変数
である。潜在変数![]() を導入し、同時確率分布
を導入し、同時確率分布![]() を考える。この分布にベイズの定理を適用すると次式を得る。
を考える。この分布にベイズの定理を適用すると次式を得る。
(1) ![]()
(2) 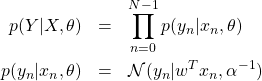
を仮定する。![]() は平均
は平均![]() 、標準偏差
、標準偏差![]() を持つ正規分布を表す。
を持つ正規分布を表す。![]() とした。
とした。![]() である。これらのパラメータに対する事前確率
である。これらのパラメータに対する事前確率![]() として次式を仮定する。
として次式を仮定する。
(3) ![]()
ここで、新たなパラメータ![]() を導入した。各確率分布を次式で定義する。
を導入した。各確率分布を次式で定義する。
(4) 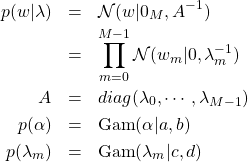
![]() はハイパーパラメータ
はハイパーパラメータ![]() を持つガンマ分布、
を持つガンマ分布、![]() は
は![]() 次元のゼロベクトル、
次元のゼロベクトル、![]() は
は![]() の対角行列である。
の対角行列である。![]() は推定すべきパラメータであり、
は推定すべきパラメータであり、![]() はエビデンス
はエビデンス![]() が最大になるように決めるハイパーパラメータである。
が最大になるように決めるハイパーパラメータである。
さて、式(2)は回帰式を
(5) ![]()
と仮定していることを意味する(ノイズ部分は無視した)。つまり、![]() は説明変数
は説明変数![]() の寄与の大きさを表す。これがベイズ推定によるARDの仕組みである。
の寄与の大きさを表す。これがベイズ推定によるARDの仕組みである。
仮定した全ての確率分布を式(1)に代入すると、次の事後確率分布を厳密に(解析的に)求めることができる。
事後確率分布![]() から、個々の説明変数の寄与の大きさを知ることができる。また、次式により未知データ
から、個々の説明変数の寄与の大きさを知ることができる。また、次式により未知データ![]() に対する
に対する![]() を予測することができる。
を予測することができる。
(6) ![]()
データ作成
回帰に用いるデータを次の手順で作成した。
(7) ![]()
説明変数![]() は目的変数
は目的変数![]() に全く寄与せず、各説明変数のスケールは大きく異なる状況をシミュレートしたものである。訓練データを100個、テストデータを30個とした。前者で学習を行い、後者で検証を行う。
に全く寄与せず、各説明変数のスケールは大きく異なる状況をシミュレートしたものである。訓練データを100個、テストデータを30個とした。前者で学習を行い、後者で検証を行う。
学習
学習の前に以下の前処理を行う。
(8) 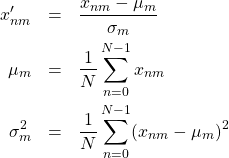
各軸(各次元)ごとに、平均値を0に標準偏差を1に正規化する。このあと、ARDを行う。Pythonライブラリsklearnに、上の「定式化」で示したロジックを実装したクラスARDRegressionがある。これを用いると、学習部分のコードは以下のようになる(ソースはここのsample_sklearn.pyである)。
|
1 2 3 4 5 6 |
def train(x, y): print("training ...") clf = ARDRegression(n_iter=1000, compute_score=True) clf.fit(x, y) print("training done!") return clf |
3行目でARDRegressionオブジェクトを作成し、4行目で学習する。次に結果を示す。
結果
最初に示すのは、![]() の平均値と標準偏差である。これは
の平均値と標準偏差である。これは![]() から求まる量である。
から求まる量である。
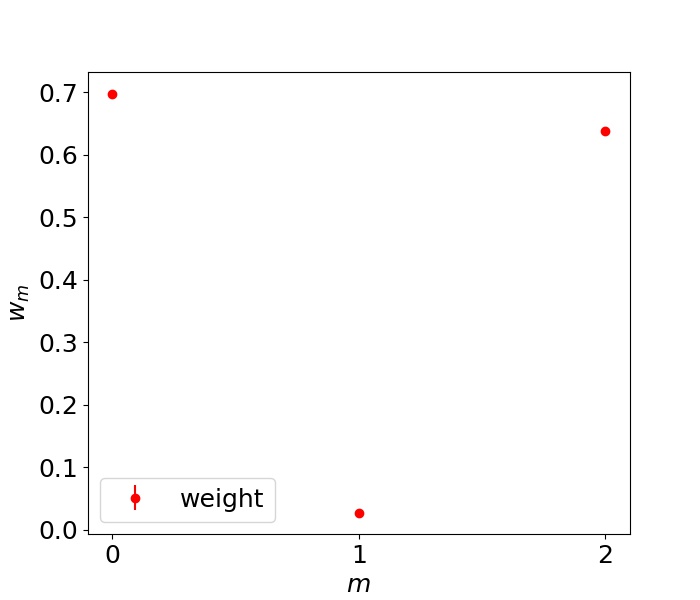
期待通りの結果である。![]() からの寄与が大きく、
からの寄与が大きく、![]() からの寄与はほとんどない。標準偏差は小さ過ぎるので上図では判別できなくなっている。次に示すのは30個のテストデータを予測した結果である。
からの寄与はほとんどない。標準偏差は小さ過ぎるので上図では判別できなくなっている。次に示すのは30個のテストデータを予測した結果である。
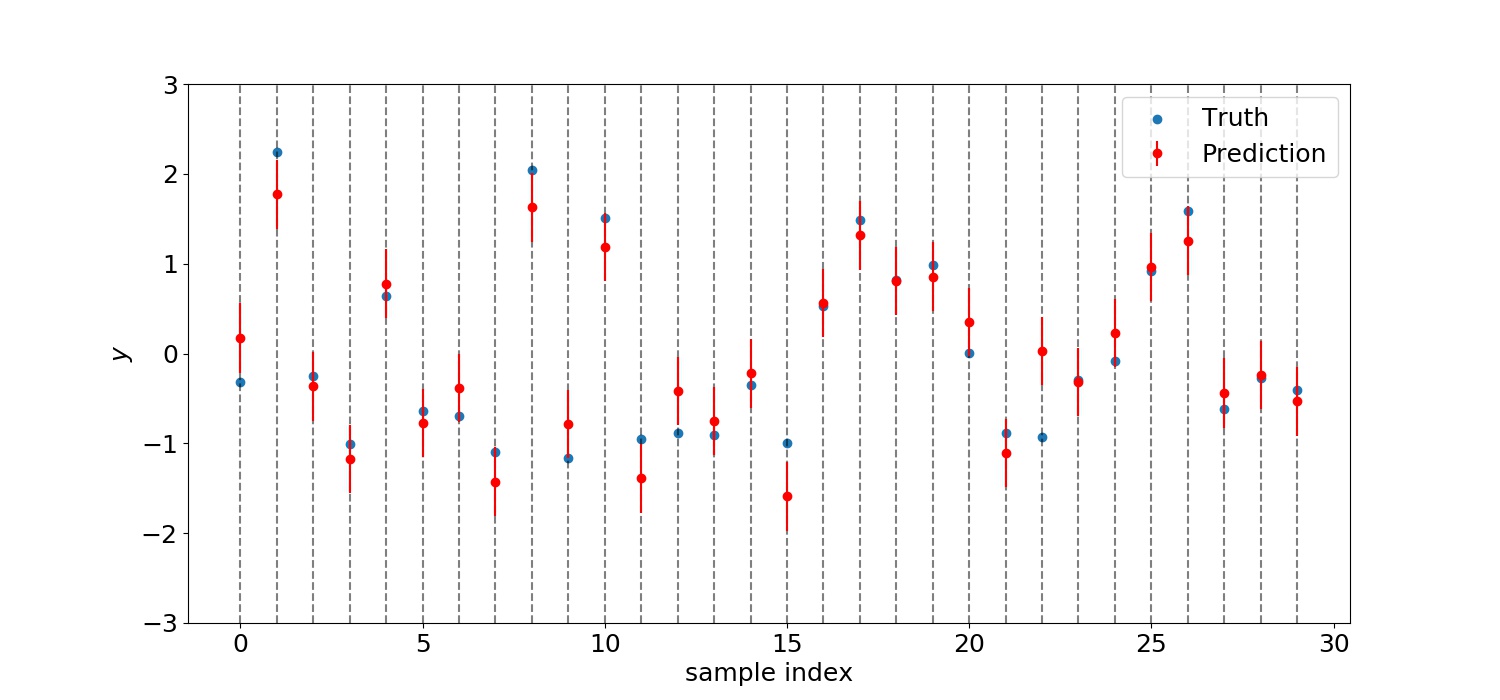
![]() の平均値は0.266となった。
の平均値は0.266となった。
ガウス過程を用いた回帰によるARD
定式化
(9) ![]()
パラメータ![]() をガウス過程に使うカーネルに関わる部分
をガウス過程に使うカーネルに関わる部分![]() とそうでない部分
とそうでない部分![]() の2つに分離する。さらに、
の2つに分離する。さらに、![]() と
と![]() の間に次式を仮定する。
の間に次式を仮定する。
(10) ![]()
ここで、![]() は平均
は平均![]() 、分散
、分散![]() の正規分布を表す。各観測値は独立同分布から生成されると仮定すると、尤度は
の正規分布を表す。各観測値は独立同分布から生成されると仮定すると、尤度は
(11) 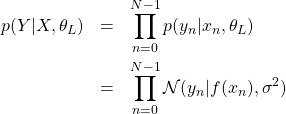
と書くことができる。ここで、![]() とした。
とした。![]() の事前分布として
の事前分布として![]() を、関数
を、関数![]() の事前分布として次のガウス過程を仮定する。
の事前分布として次のガウス過程を仮定する。
(12) ![]()
ここで、![]() とした。
とした。![]() は
は![]() 次元のゼロベクトル、
次元のゼロベクトル、![]() はパラメータ
はパラメータ![]() を持つ
を持つ![]() の共分散行列、その成分
の共分散行列、その成分![]() がカーネル関数となる。カーネル関数として次のものを用いる。
がカーネル関数となる。カーネル関数として次のものを用いる。
(13) 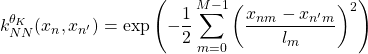
ここで、![]() とした。
とした。![]() は各軸のスケール長を表す。この逆数が説明変数の重みに相当する。さらに、
は各軸のスケール長を表す。この逆数が説明変数の重みに相当する。さらに、![]() の事前分布
の事前分布![]() も導入する。ここまでの結果をまとめると、式(9)は次のようになる。
も導入する。ここまでの結果をまとめると、式(9)は次のようになる。
(14) ![]()
![]() の事前分布
の事前分布![]() がガウス過程であることに注意する。上式をベイズ推定により評価することもできるが、ここでは右辺分子を取り出しMAP推定を行う。右辺分子の対数を取ると
がガウス過程であることに注意する。上式をベイズ推定により評価することもできるが、ここでは右辺分子を取り出しMAP推定を行う。右辺分子の対数を取ると
(15) ![]()
を得る。これを最大にするような![]() と
と![]() を求める。
を求める。
(16) ![]()
この2つのパラメータについては点推定であることに注意する(確率を求めるのではない)。未知の値![]() に対する
に対する![]() の確率分布は次式から計算される。
の確率分布は次式から計算される。
(17) ![]()
右辺の積分内の最初の項![]() は
は![]() を表し、式(12)から解析的に求めることができる条件付き確率分布である。上式から
を表し、式(12)から解析的に求めることができる条件付き確率分布である。上式から![]() の分布が分かれば、未知の値
の分布が分かれば、未知の値![]() に対する
に対する![]() の値は次式から決定することができる。
の値は次式から決定することができる。
(18) 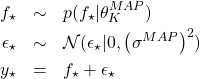
以上で定式化できたので、実際に計算を行う。
学習
上の定式化で示したロジックは、ガウス過程のためのPythonライブラリGPyに実装されている。先と同じデータを使用し、先と同じ前処理を施したあと、以下を実行する(ソースはここのsample_gp_multi_dim.ipynbである)。
|
1 2 3 4 5 6 7 8 9 |
# カーネルを定義する。 kernel = GPy.kern.RBF(input_dim=n_features, variance=0.01, ARD=True) # kernel = GPy.kern.Matern52(n_features, ARD=True) # ガウス過程を用いた回帰を行う。 model = GPy.models.GPRegression(train_xs, train_ys, kernel) # 最適化(MAP推定)を行う。 model.optimize(messages=True, max_iters=1e5) |
2行目でカーネル関数(式(13)に相当する)を定義し、6行目と9行目でガウス過程による回帰を行う(ベイズ推定ではなくMAP推定が行われる)。
結果
最初に重み![]() の値を示す。
の値を示す。

期待通りの結果である。![]() からの寄与が大きく、
からの寄与が大きく、![]() からの寄与はほとんどない。
からの寄与はほとんどない。![]() は点推定される量であるから、「ベイズ推定を用いた回帰によるARD」の場合とは異なり標準偏差は存在しないことに注意する。次に、テストデータを予測した結果を示す。
は点推定される量であるから、「ベイズ推定を用いた回帰によるARD」の場合とは異なり標準偏差は存在しないことに注意する。次に、テストデータを予測した結果を示す。
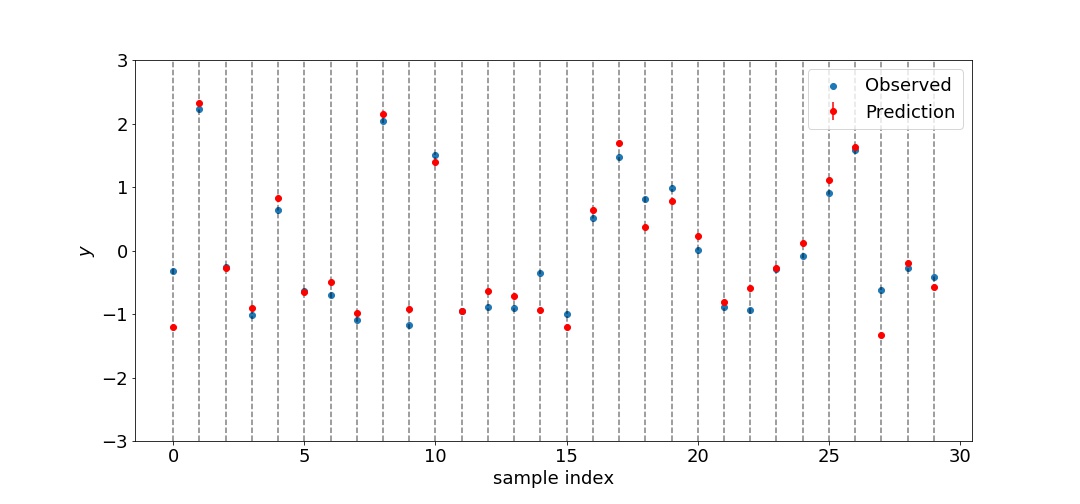
標準偏差は小さ過ぎて上図では判別できなくなっている。![]() の平均値は0.212となった。「ベイズ推定を用いた回帰によるARD」のときは0.266であったから改善されている。ガウス過程の場合、非線形回帰となるため精度が上がるのだろう。
の平均値は0.212となった。「ベイズ推定を用いた回帰によるARD」のときは0.266であったから改善されている。ガウス過程の場合、非線形回帰となるため精度が上がるのだろう。
まとめ
今回は、2つの文脈でAutomatic Relevance Determination(ARD)を見た。
- ベイズ推定を用いた回帰によるARD
- ガウス過程を用いた回帰によるARD
1の回帰は線形回帰であるが、2の回帰は非線形回帰である。今回のデータに対しては、予測精度は2の方が高い。また、1の計算では![]() の行列を、2の計算では
の行列を、2の計算では![]() の行列を扱う。したがって、今回のような
の行列を扱う。したがって、今回のような![]() の場合は、1の方が高速に計算できる。
の場合は、1の方が高速に計算できる。

