はじめに
機械学習の目的は、観測データを元に未知データを予測できるモデル(予測モデル)を作ることである。予測モデルの実体はパラメータを含む数式なので、観測データと良く合い、かつ汎化能力が高くなるようにパラメータを決定することになる。パラメータの値自体は学習により決まるが、パラメータをいくつ導入するかはユーザがあらかじめ決めなければならない。今回は、パラメータの数の最適化に使うことのできる情報量規準(AICとBIC)について解説する。
情報量規準
観測値として![]() が与えられたとき、予測モデルとして条件付き確率
が与えられたとき、予測モデルとして条件付き確率![]() を仮定したとする。
を仮定したとする。![]() はパラメータの集合
はパラメータの集合![]() を表す。各パラメータの値自体は学習により決まるが、パラメータの数
を表す。各パラメータの値自体は学習により決まるが、パラメータの数![]() はユーザがあらかじめ決める必要がある。
はユーザがあらかじめ決める必要がある。![]() を大きくするような
を大きくするような![]() を選べば良いが、観測データ
を選べば良いが、観測データ![]() に対し
に対し![]() が最大となるように
が最大となるように![]() を選択してしまうと、未知のデータに対する精度が悪くなる現象が起きる。これを過学習と呼ぶ。機械学習の目的は未知データに対する精度を高くする(汎化能力を高める)ことであるから、何らかの対処が必要になる。
を選択してしまうと、未知のデータに対する精度が悪くなる現象が起きる。これを過学習と呼ぶ。機械学習の目的は未知データに対する精度を高くする(汎化能力を高める)ことであるから、何らかの対処が必要になる。
一般に、パラメータの数(今の場合![]() )が多いほどモデルの表現能力は高まり、複雑な観測データの分布を精度良く再現できるようになる。しかし、観測データに特化したモデルになるため未知データに対する予測精度が悪くなる。従って、パラメータの数を減らしモデルの表現能力を落としつつ(観測データの精度を犠牲にしつつ)、未知データに対する予測精度を上げることを目指す必要がある。このとき、パラメータの数(
)が多いほどモデルの表現能力は高まり、複雑な観測データの分布を精度良く再現できるようになる。しかし、観測データに特化したモデルになるため未知データに対する予測精度が悪くなる。従って、パラメータの数を減らしモデルの表現能力を落としつつ(観測データの精度を犠牲にしつつ)、未知データに対する予測精度を上げることを目指す必要がある。このとき、パラメータの数(![]() )をいくつにするのが一番良いのかを決める評価規準があると便利である。この規準を作るため、まず最初に観測データ
)をいくつにするのが一番良いのかを決める評価規準があると便利である。この規準を作るため、まず最初に観測データ![]() の再現率を最大化(
の再現率を最大化(![]() を最大化)する規準を作る。
を最大化)する規準を作る。
![]()
慣習上、最小となる量にしたいので負号を付け、さらに係数2を付ける。
![]()
対数を取るのは計算が楽になる場合が多いためである。係数2を付けた理由は、確率として正規分布を想定する場合が多く、その際に指数の肩の係数を相殺したいためである。![]() は確率であるが、
は確率であるが、![]() の関数とみるときは尤度と呼ばれる。従って、上の規準は「負の対数尤度を最小化する」規準となる。さて、既に述べたように、観測データ
の関数とみるときは尤度と呼ばれる。従って、上の規準は「負の対数尤度を最小化する」規準となる。さて、既に述べたように、観測データ![]() に対し尤度を最大化してしまうと汎化能力の低いものになってしまう。そこで、パラメータ数
に対し尤度を最大化してしまうと汎化能力の低いものになってしまう。そこで、パラメータ数![]() の増加に伴うペナルティ項を追加する。
の増加に伴うペナルティ項を追加する。
![]()
この規準を赤池情報量規準(Akaike’s Information Criterion:AIC)と呼ぶ。パラメータ数![]() に関わるペナルティとしては別の項を用いる場合がある。
に関わるペナルティとしては別の項を用いる場合がある。
![]()
こちらはベイズ情報量規準(Bayesian Information Criterion:BIC)と呼ばれる。![]() だけでなく観測データ数
だけでなく観測データ数![]() も含まれることに注意する。この2つの規準が、最適なパラメータ数を決める指標として良く使われる。
も含まれることに注意する。この2つの規準が、最適なパラメータ数を決める指標として良く使われる。
回帰の場合
具体的な事例を見るため回帰を考える。![]() の成分
の成分![]() を2次元ベクトル
を2次元ベクトル![]() とみなし、
とみなし、![]() の関数形を求める問題を考える。
の関数形を求める問題を考える。
(1) 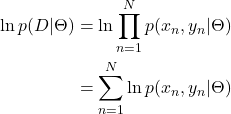
ここで、データは独立に同一の確率分布から生成されることを仮定した。いま![]() として正規分布を仮定する(簡単のため1次元を考える)。
として正規分布を仮定する(簡単のため1次元を考える)。
![]()
ここで![]() は次式で定義される量である。
は次式で定義される量である。
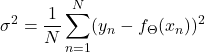
これは、予測値![]() と観測値
と観測値![]() との間のずれを記述する分散である。これらを式(1)の最右辺に代入すると
との間のずれを記述する分散である。これらを式(1)の最右辺に代入すると
(2) ![]()
を得る。式(2)を用いて![]() と
と![]() を書くと
を書くと
(3) ![Rendered by QuickLaTeX.com \begin{align*} C_{\rm AIC}&={\rm arg}\min_{M}\rBigf[N\ln{\sigma^2}+2M\lBig]\\ C_{\rm BIC}&={\rm arg}\min_{M}\rBigf[N\ln{\sigma^2}+M\ln{N}\lBig] \end{align*}](/wp-content/ql-cache/quicklatex.com-d27f576f72f212e440fba898d24d65ee_l3.png)
となる。ただし、定数項は落とした。![]() と
と![]() のどちらの規準に対しても、第1項は予測値と観測値の間のずれが小さいほど小さくなる量である。この項はモデルが複雑になるほど(パラメータ数
のどちらの規準に対しても、第1項は予測値と観測値の間のずれが小さいほど小さくなる量である。この項はモデルが複雑になるほど(パラメータ数![]() が増えるほど)小さくなる。一方、第2項はパラメータ数
が増えるほど)小さくなる。一方、第2項はパラメータ数![]() が増えるほど大きくなる量である。これらのトレードオフで適切な
が増えるほど大きくなる量である。これらのトレードオフで適切な![]() が決まる。
が決まる。
実験
ここまでの説明を実際のコード(ここ)で確認する。最初に観測データを人工的に作る。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def calculate_ground_truth(xs: NDArray[np.float64]) -> NDArray[np.float64]: return 2.0 * xs - np.sin(3.0 * np.pi * xs) def make_dataset(n: int, scale: float) -> List[NDArray[np.float64]]: xs = np.linspace(start=0, stop=1, num=50) ys = polynomial(xs) random_xs = np.random.rand(n) random_ys = calculate_ground_truth(random_xs) + np.random.normal( loc=0, scale=scale, size=n ) return [xs, ys, random_xs, random_ys] |
(4) ![]()
9,10,11行目でこの式にノイズを加えている。グラフは以下の通り。
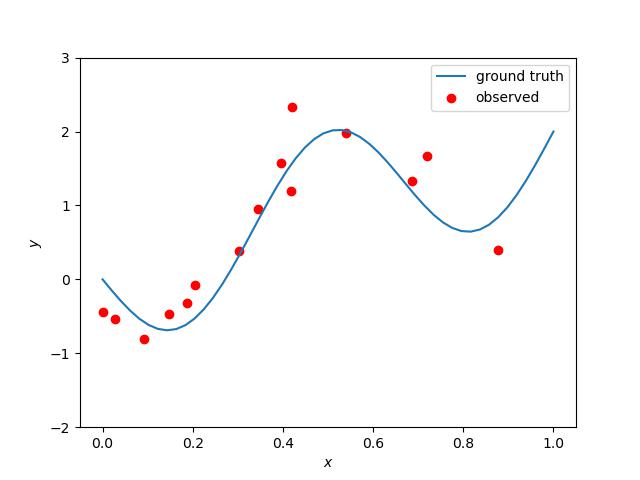
赤点が人工的に発生させた観測点(15個)である。青い曲線は式(4)である。次に![]() の形を具体的に決める必要がある。ここでは次の多項式を採用する。
の形を具体的に決める必要がある。ここでは次の多項式を採用する。
(5) 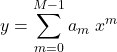
このとき、![]() となる。コードではsklearnの関数を用いた。
となる。コードではsklearnの関数を用いた。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def execute_regression( xs: NDArray[np.float64], ys: NDArray[np.float64], degree: int ) -> Tuple[LinearRegression, PolynomialFeatures]: # 次元を追加(ライブラリの仕様に合わせる) xs = xs[:, np.newaxis] ys = ys[:, np.newaxis] polynomial_features = PolynomialFeatures(degree=degree) xs_poly = polynomial_features.fit_transform(xs) model = LinearRegression() model.fit(xs_poly, ys) return model, polynomial_features |
上のコード中のdegreeが![]() に相当する。8行目で多項式を定義し、10行目と11行目で回帰を行っている。次に、最適な
に相当する。8行目で多項式を定義し、10行目と11行目で回帰を行っている。次に、最適なdegreeを探すためAICとBICを計算する。
|
1 2 3 4 5 |
def calculate_aic_and_bic( mse: np.float64, degree: int, data_num: int ) -> Tuple[np.float64, np.float64]: a = data_num * np.log(mse) return (a + 2 * degree, a + degree * np.log(data_num)) |
5行目のタプルの最初の項がAIC、次の項がBICである。式(3)をそのままコードにしただけである。AICとBICのdegree依存性は以下の通り。
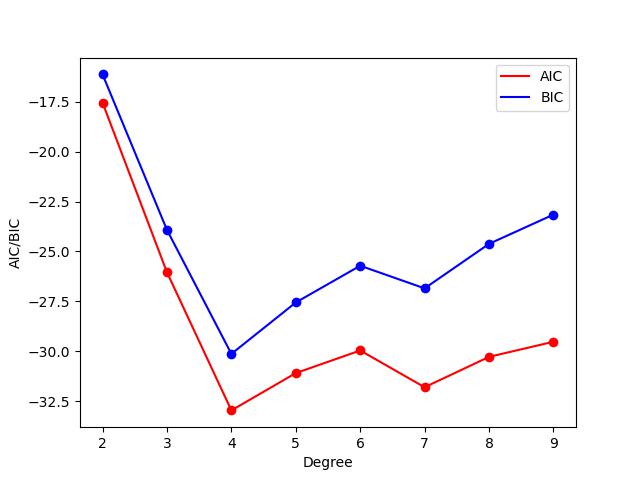
AICとBICのいずれの規準に対してもDegree(=![]() )が4のとき最小値となっている。
)が4のとき最小値となっている。Degree=3,4,5として多項式を描画すると以下になる。
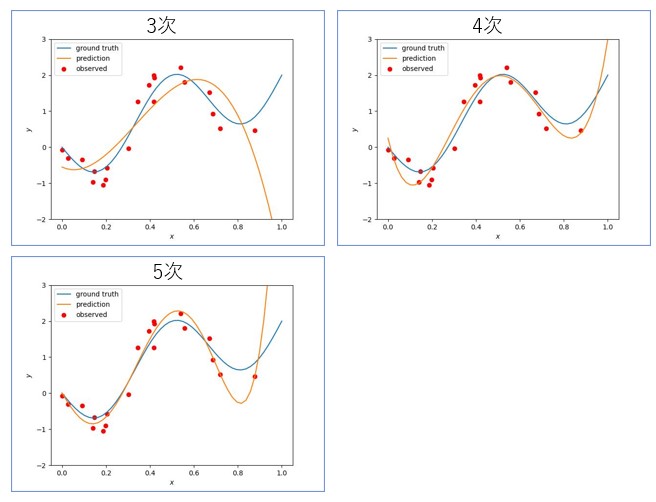
橙色の曲線が予測した曲線、青い曲線が真の曲線、赤点が観測点である。3次よりは4次の方が良いことは明らかだが、4次と5次を比較した場合は迷う。このような場合にAICやBICのような規準が力が発揮する。今回は4次を選択すべきというご託宣である。AICとBICの結果が同じ(4次がベスト)になったのはたまたまである。
AICとBICの違い
AICやBICで比較するモデルの集合の中に、真のモデルが含まれていると仮定する。このとき、観測データ数を無限大にしたとき真のモデルが必ず選ばれることを「一致性を持つ」と言う。一方、比較するモデル集合の中に真のモデルが含まれていない場合、観測データ数を無限大にしたとき、最も誤差を小さくするモデルが選ばれることを「有効性を持つ」と言う。このとき以下の事実が知られている。
従って、AICとBICのどちらが優れているかは一概には言えない。
まとめ
今回は数ある情報量規準のうち、AICとBICを紹介した。今回は、たまたまAICとBICの結果が一致したが、異なる場合は解析者の判断に委ねられることが多い。ところで、いま深層学習で主流のモデルは億単位のパラメータ数を持つ。最近の研究によると、パラメータ数を増やせば増やすほど精度も上がるそうである。この事実と今回紹介した情報量規準はどう関係するのであろうか。

