はじめに
今回は時系列解析シリーズの最終回として、実際のデータを解析する。ソースコードはこのファルダ内にあるsrc/main_for_blog.ipynbである。言語はPythonである。
使用データ
使用するデータはこれである。1949年1月から1960年12月までの飛行機の乗客数データである。グラフは以下の通り。
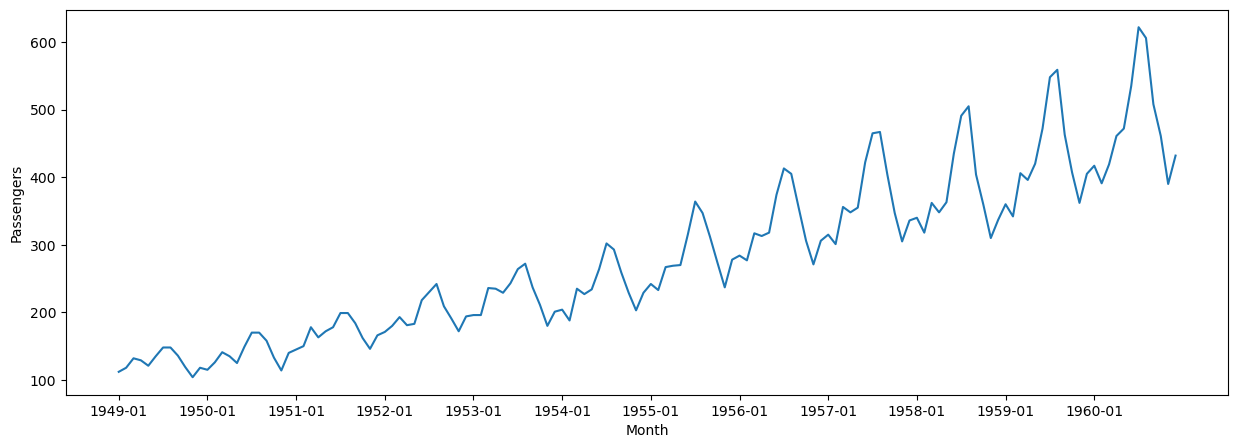
図1
単調増加しており一目で非定常過程であることが分かる。
解析手順
解析手順は以下の通り。
- 非定常過程から定常過程に変換する。
- 自己相関を描画し周期を同定する。
- 訓練データとテストデータに分割する。
- 訓練データでハイパーパラメータを最適化する。
- 訓練データで訓練する。
- テストデータで予測する。
まず最初に、定常過程への変換から始める。
定常過程へ
定常過程に変換するために必要な差分回数を見積もる。最初に原系列に対しKPSS検定を行う。
|
1 2 3 4 5 6 7 8 |
import statsmodels.api as sm # 原系列に対して kpss_stat, p_value, lags, crit = sm.tsa.kpss(data["#Passengers"]) print(f"kpss_stat: {kpss_stat}") print(f"p_value: {p_value}") print(f"lags: {lags}") print(f"cirt: {crit}") |
4行目でモジュールstatsmodels内の関数kpssを使っている。上のコードを実行するとp_valueとして0.01を得た。この値は0.05(5%)より小さいから単位根ありと判定できる。つまり差分を取れる。次に1階差分系列に対しKPSS検定を行う。
|
1 2 3 4 5 6 |
diff_data = data["#Passengers"].diff(periods=1).dropna() kpss_stat, p_value, lags, crit = sm.tsa.kpss(diff_data) print(f"kpss_stat: {kpss_stat}") print(f"p_value: {p_value}") print(f"lags: {lags}") print(f"cirt: {crit}") |
1行目のdiff関数で1階差分を取っている。上のコードを実行するとp_valueは0.1となった。この値は0.05より大きいから単位根なしと判定できる。つまりこれ以上差分を取る必要はないということである。ここまでの結果から、原系列は単位根過程であることが分かり、差分回数は1と結論される。ところで、差分回数は別の関数でも評価できる。
|
1 2 3 4 |
from pmdarima import arima d = arima.ndiffs(data["#Passengers"]) print(f"d: {d}") |
モジュールpmdarimaの関数ndiffsを使うことができる。dが差分回数である。上を実行するとd=1を得る。この関数内部でもKPSS検定が行われている。
周期の検出
差分系列の自己相関を描画する。
|
1 2 3 4 5 |
fig = plt.figure(figsize=(15, 5)) ax1 = fig.add_subplot(111) ax1.set_xticks(range(0, len(data), 12)) fig = sm.graphics.tsa.plot_acf(diff_data, lags=100, ax=ax1) plt.savefig("..//images//acf_diff_1.png") |
4行目の関数plot_acfで自己相関のグラフを描画している。出力は以下の通り。
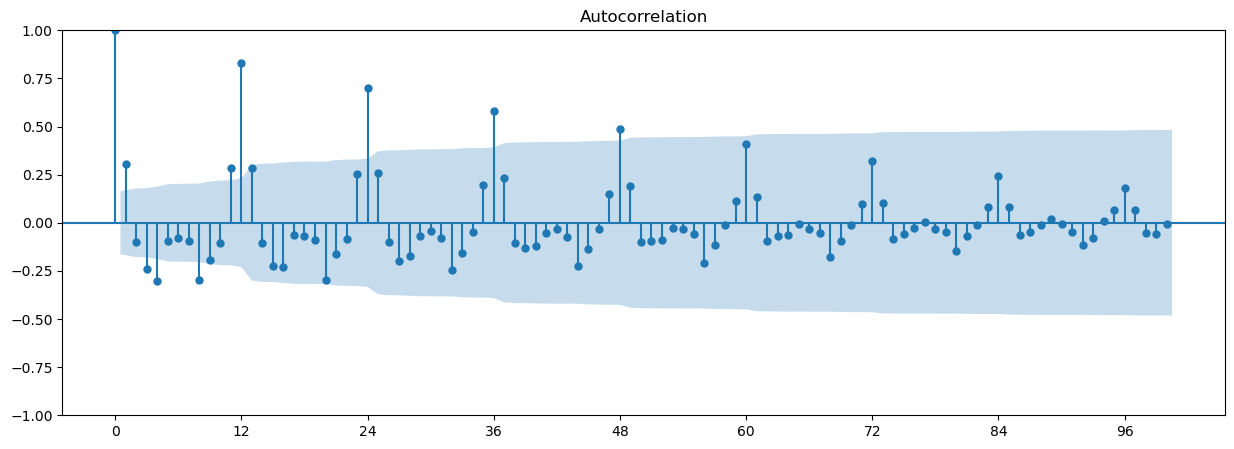
図2
12ヵ月周期であることが分かる。
訓練データとテストデータへの分割
次のコードでデータを分割する。今回は全データの8割を訓練データとした。
|
1 2 3 4 |
from pmdarima import model_selection df_train, df_test = model_selection.train_test_split(data, train_size=0.8) print(f"training data size: {len(df_train)}") print(f"test data size: {len(df_test)}") |
出力は以下の通り。
|
1 2 |
training data size: 115 test data size: 29 |
ハイパーパラメータの最適化
今回使う時系列モデルはSARIMAである。このモデルのパラメータは、![]() と
と![]() であった。ここまでの解析で差分回数
であった。ここまでの解析で差分回数![]() と周期
と周期![]() は分かっている。ここでは残りのハイパーパラメータをグリッドサーチで最適化する。
は分かっている。ここでは残りのハイパーパラメータをグリッドサーチで最適化する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
def execute_grid_search( ts_train: pd.DataFrame, d: int, m: int ) -> list[Tuple3Int, Tuple4Int, np.float64]: # SARIMA(p,d,q)(sp,sd,sq)[s]の次数の範囲を決める。 p = q = range(0, 3) if m == 0: sp = sd = sq = range(0, 1) else: sp = sd = sq = range(0, 2) # グリッドサーチのために、p,q,sp,sd,sqの組み合わせのリストを作成する。 # 定常性の確認よりd=1,周期sは決め打ちで12としている。 pdq = [(x[0], d, x[1]) for x in list(itertools.product(p, q))] seasonal_pdq = [(x[0], x[1], x[2], m) for x in list(itertools.product(sp, sd, sq))] best_result = [0, 0, 10000000] for param in pdq: for param_seasonal in seasonal_pdq: try: mod = SARIMAX( ts_train, order=param, seasonal_order=param_seasonal, enforce_stationarity=True, enforce_invertibility=True, ) results = mod.fit() print("order{}, s_order{} - AIC: {}".format(param, param_seasonal, results.aic)) if results.aic < best_result[2]: best_result = [ param, # type:ignore param_seasonal, # type:ignore results.aic, ] except Exception: print("Exception!") continue return best_result |
上の関数を用いて以下を実行する。
|
1 2 3 4 5 6 7 |
import utils d = 1 m = 12 best_result = utils.execute_grid_search(df_train["#Passengers"], d, m) a = best_result[0] A = best_result[1] print(f"> best model(p,d,q),(P,D,Q,m),AIC: {best_result}") |
結果は以下の通り。
|
1 |
> best model(p,d,q),(P,D,Q,m),AIC: [(2, 1, 2), (0, 1, 0, 12), 755.2007099265888] |
AICは赤池情報量規準である。AICが最小になるように最適化される。
訓練
上のハイパーパラメータを用いてモデルを訓練する。
|
1 2 3 4 5 |
def train(ts_train: pd.DataFrame, a: tuple[int, ...], A: tuple[int, ...]) -> SARIMAXResultsWrapper: (p, d, q) = a (P, D, Q, m) = A model = SARIMAX(endog=ts_train, order=(p, d, q), seasonal_order=(P, D, Q, m)).fit() return model |
4行目で、モジュールstatsmodelsが持つクラスSARIMAXのインスタンスを作成し訓練を実行している。ここで、SARIMAXのXは外生変数を表す。気温や天気など元の時系列データには含まれない外部要因を考慮できるようにSARIMAを拡張したモデルがSARIMAXである。ここでは外生変数は考えない。上の関数を用いて下のコードで訓練を実行する。
|
1 |
model = utils.train(df_train["#Passengers"], a, A) |
予測
訓練済みモデルmodelを用いて予測を行う。
|
1 2 3 4 5 6 7 8 |
def predict( arima_model: SARIMAXResultsWrapper, df_test: pd.DataFrame ) -> tuple[pd.Series, pd.Series, pd.DataFrame]: # predict train_pred = arima_model.predict() test_pred = arima_model.forecast(len(df_test)) test_pred_ci = arima_model.get_forecast(len(df_test)).conf_int() return (train_pred, test_pred, test_pred_ci) |
5行目の関数predictは訓練期間の予測である。6行目のforecastでテスト期間の予測をしている。1行目の関数predictを用いて以下のコードで予測する。
|
1 |
train_pred, test_pred, test_pred_ci = utils.predict(model, df_test) |
返り値であるtrain_predは訓練期間に対する予測値、test_predはテスト期間に対する予測値、test_pred_ciはテスト期間に対する信頼区間である。グラフは以下の通り。垂直な点線の左側が訓練期間、右側がテスト期間である。
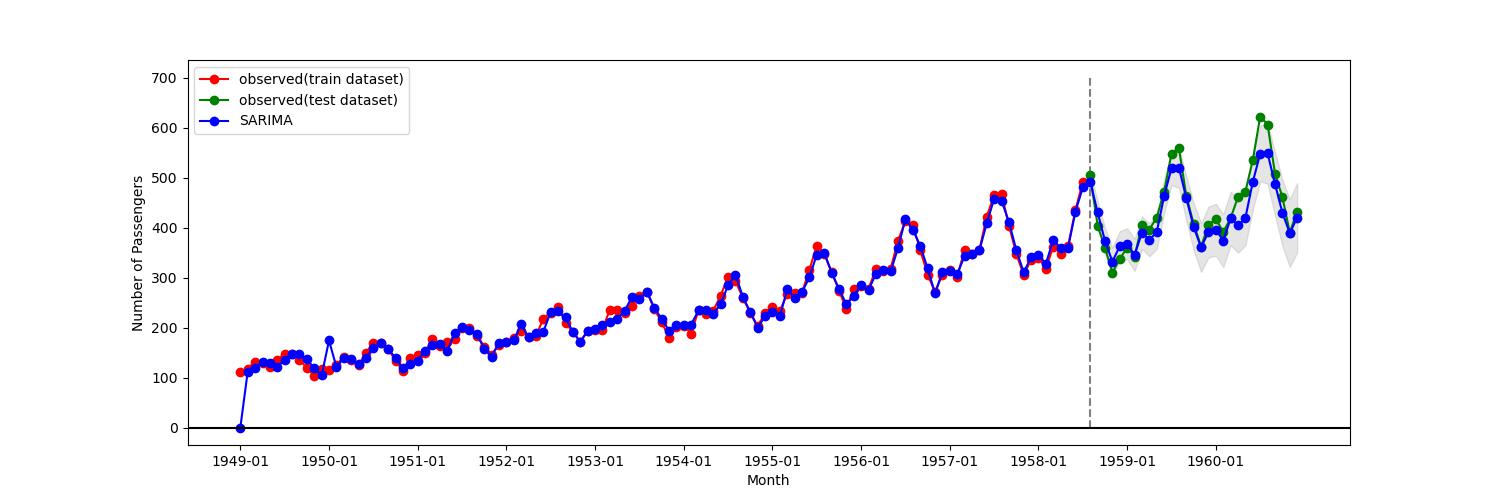
図3
赤色が訓練期間の観測値、緑色がテスト期間の観測値、青色がSARIMAXによる予測値である。網掛け部分が予測時の信頼区間を表す。テスト期間を拡大したものを以下に示す。
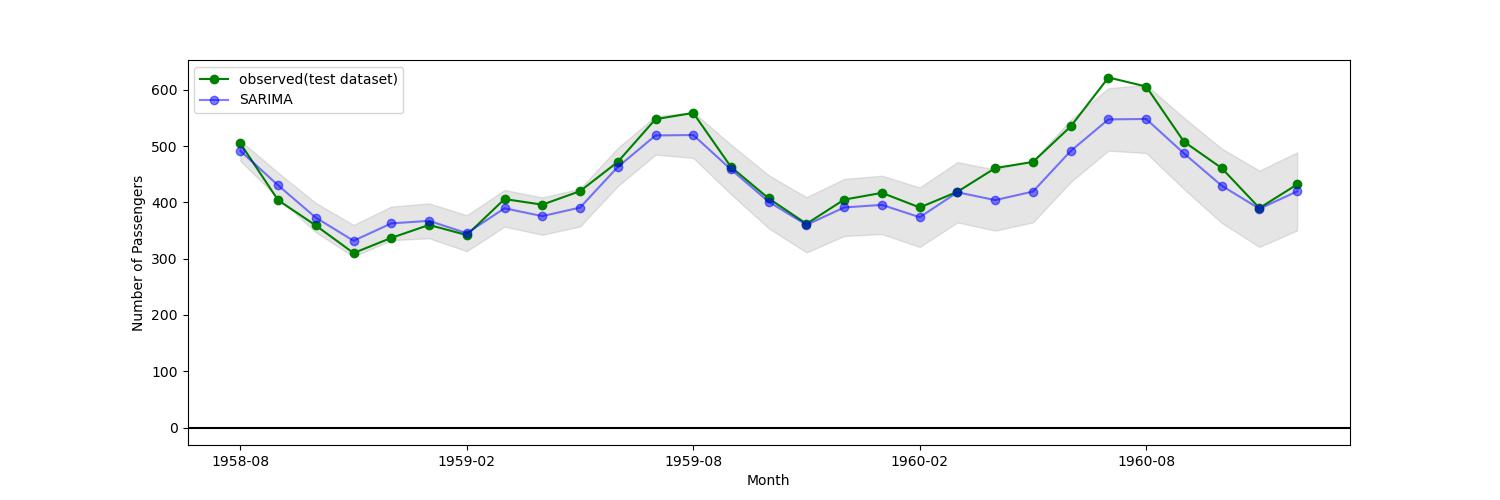
図4
青色が予測値、緑色が観測値、網掛けが信頼区間である。
まとめ
今回使用したSARIMAモデルは、解析手順が確立しており大変扱いやすい手法である。ライブラリも充実しているので手軽に試すことができる。時系列解析において最初に試すことができる手法であろう。
参照サイト

