はじめに
最近、法線ベクトルを求める機会があった。Point Cloud Library(PCL)が提供する関数を使えば簡単に求めることができる。法線ベクトルを求めるアルゴリズムについてもここに説明があるが、結果の式しか記載されていない。今回はこの式の導出を行う。
問題設定
いま、3次元空間内に存在する点群を考える。この点群はなんらかの物体の表面から取得されたものである。点群だけから物体の表面を推測し、表面上の各点における法線ベクトルを求めたい。
方針
点群から法線を求める方法には2つある。
- 点群から曲面を求め、その曲面から各点の法線を計算する。
- 点群から直接法線を計算する。
前者では、点を結ぶ小さな三角形をたくさん作る(ポリゴン化)。ノイズの載った点が混じると凸凹した表面が出来上がるため、ノイズに弱い手法である。一方、後者では、対象点近傍の点を複数個考慮し法線を求めるため、ノイズの効果は相対的に小さくなる(後述)。PCLが採用している手法は後者であり、その手順は以下の通りである。
- ある点
 を考える。
を考える。 - 点
 の近傍
の近傍 個の点を考える。
個の点を考える。 - 点
 と近傍
と近傍 個の点を使い、最小自乗法により平面を決定する。
個の点を使い、最小自乗法により平面を決定する。 - その平面の法線ベクトルを求める。
以下この方針に従って法線ベクトルを求める。
導出
点![]() 近傍の
近傍の![]() 個の点の集合を
個の点の集合を![]() と書くことにする。点群
と書くことにする。点群![]() が近似する平面
が近似する平面![]() の法線を
の法線を![]() と書くと、平面
と書くと、平面![]() 上の点
上の点![]() は次式を満たす。
は次式を満たす。
(1) ![]()
ここで、![]() は定数である。点群
は定数である。点群![]() が平面
が平面![]() を近似するには次を最小にすれば良い。
を近似するには次を最小にすれば良い。
(2) 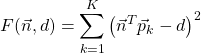
上式を最小にするような![]() を求める。平面の式(1)には定数倍だけの不定性がある。これを取り除くため、
を求める。平面の式(1)には定数倍だけの不定性がある。これを取り除くため、![]() の大きさを1に限定する条件を、Lagrangeの未定係数法により導入する。
の大きさを1に限定する条件を、Lagrangeの未定係数法により導入する。
(3) 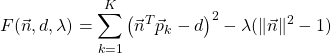
ここで、![]() もまた
もまた![]() を最小化するように決定すべきパラメータである。最初に、
を最小化するように決定すべきパラメータである。最初に、![]() を
を![]() で偏微分し0とおくことにより次式を得る。
で偏微分し0とおくことにより次式を得る。
(4) 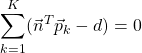
(5) 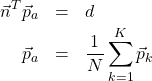
![]() は点群
は点群![]() の重心である。上式を式(3)に代入すると
の重心である。上式を式(3)に代入すると
(6) ![Rendered by QuickLaTeX.com \begin{equation*} F(\vec{n},\lambda)=\sum_{k=1}^{K}\left[\vec{n}^T(\vec{p}_k-\vec{p}_a)\right]^2-\lambda(\|\vec{n}\|^2-1) \end{equation*}](/wp-content/ql-cache/quicklatex.com-2b6463d6d1d284ff4ff6461c3d6604d9_l3.png)
を得る。これを今度は![]() で偏微分し0とおくことにより次式を得る。
で偏微分し0とおくことにより次式を得る。
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \left[\vec{n}^T\sum_{k=1}^K\left(\vec{p}_k-\vec{p}_a\right)\right]\left(\vec{p}_k-\vec{p}_a\right)=\lambda\vec{n} \end{equation*}](/wp-content/ql-cache/quicklatex.com-7a957eb664a7e0de1f6c0665227c277a_l3.png)
上の式は少し分かり難いので説明しておく。[]で囲われた部分は内積であり、スカラー量となる。従って上式左辺は全体としてベクトル量になる。また、添字![]() についての和は内積部分だけで閉じておらず、後ろの
についての和は内積部分だけで閉じておらず、後ろの![]() にもかかっていることに注意する。さて、式(7)は以下のように変形できる。
にもかかっていることに注意する。さて、式(7)は以下のように変形できる。
(8) 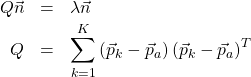
この式は、点群![]() の共分散行列
の共分散行列![]() の固有値を求める式である。つまり、法線の導出問題が共分散行列
の固有値を求める式である。つまり、法線の導出問題が共分散行列![]() の固有値問題に帰着したことになる。これが、ここに記載されている式である。いま考えている空間は3次元であるから
の固有値問題に帰着したことになる。これが、ここに記載されている式である。いま考えている空間は3次元であるから![]() は
は![]() の行列である。さて、式(2)に式(5)を代入すると
の行列である。さて、式(2)に式(5)を代入すると
(9) ![Rendered by QuickLaTeX.com \begin{equation*} F(\vec{n})=\sum_{k=1}^{K}\left[\vec{n}^T\left(\vec{p}_k-\vec{p}_a\right)\right]^2 \end{equation*}](/wp-content/ql-cache/quicklatex.com-4759770e768792803a66fe3f29483aea_l3.png)
を得る。![]() を使って上式を書き直すと
を使って上式を書き直すと
(10) 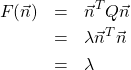
となる。ここで、![]() を用いた。つまり、
を用いた。つまり、![]() を最小にするには、複数の固有値のうち最小のものを選択すれば良いことになる(いまの場合、非ゼロの固有値は最大で3つ求まる)。その固有値に対応する固有ベクトルが求めたい法線ベクトルである。
を最小にするには、複数の固有値のうち最小のものを選択すれば良いことになる(いまの場合、非ゼロの固有値は最大で3つ求まる)。その固有値に対応する固有ベクトルが求めたい法線ベクトルである。
主成分分析との関係
式(8)は、点群![]() の位置座標について主成分分析を行う際に出てくる式である。得られる3つの主成分のうち一番小さい寄与を持つ方向が法線に対応するわけである。
の位置座標について主成分分析を行う際に出てくる式である。得られる3つの主成分のうち一番小さい寄与を持つ方向が法線に対応するわけである。
まとめ
今回はPoint Cloud Library(PCL)が提供する法線ベクトル導出アルゴリズムを定式化した。PCLを用いた法線導出のサンプルコードはここを見てほしい。ここでは適用結果だけを示す。

法線![]() の3成分をRGBに対応させた画像である。今回用いた3Dモデルの場合、近傍点の数
の3成分をRGBに対応させた画像である。今回用いた3Dモデルの場合、近傍点の数![]() を20個程度にすると上のような綺麗な法線,法線ベクトル,点群(法線が滑らかに変化する)画像となった。
を20個程度にすると上のような綺麗な法線,法線ベクトル,点群(法線が滑らかに変化する)画像となった。

