はじめに
今回はLevel Set法と呼ばれるアルゴリズムを紹介し、その実行例を示す。
Level Set法とは
最初に、画像にLevel Set法を適用した結果を示す(動画)。
上の動画のように、初期閉曲線を物体の縁に沿って成長させていく仕組みがLevel Set法である。本手法は2Dの画像だけでなく3D物体に対しても適用できる(3D物体への適用例)。Level Set法は任意次元に適用できる汎用性の高い輪郭抽出アルゴリズムである。
アルゴリズム
Level Set法は、![]() 次元空間内に存在する物体の境界面を、
次元空間内に存在する物体の境界面を、![]() 次元空間内の曲面(超曲面)を時間発展させることにより検出する手法である。
次元空間内の曲面(超曲面)を時間発展させることにより検出する手法である。![]() のときの様子を以下に示す。
のときの様子を以下に示す。
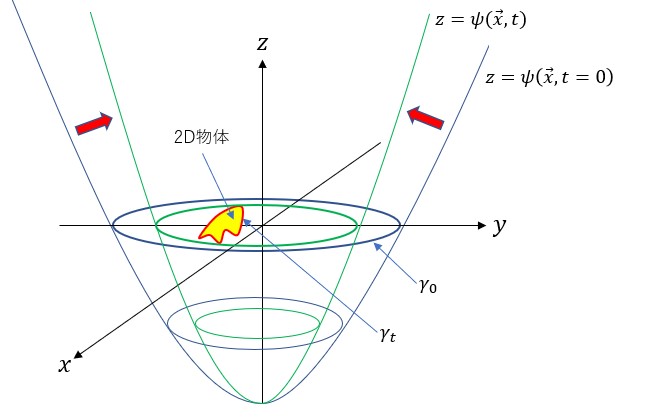
右図の黄色の物体は![]() 平面内にあるとする。最初にこの物体を囲む閉曲線
平面内にあるとする。最初にこの物体を囲む閉曲線![]() を
を![]() 平面内に作り、この閉曲線を用いて曲面
平面内に作り、この閉曲線を用いて曲面![]() を作る(作り方は後述)。この曲面と
を作る(作り方は後述)。この曲面と![]() 平面との交線が閉曲線
平面との交線が閉曲線![]() である。さて、この曲面を内側に向かって少しずつ収縮させていく。収縮時の速度は物体との距離が縮まるにつれ小さくなるように定義される。速度が0になったときの曲面
である。さて、この曲面を内側に向かって少しずつ収縮させていく。収縮時の速度は物体との距離が縮まるにつれ小さくなるように定義される。速度が0になったときの曲面![]() と
と![]() 平面との交線が物体の境界線
平面との交線が物体の境界線![]() (赤線)である。Level Set法は、対象とする空間(今の場合2次元)より1次元高い空間(今の場合3次元)内の曲面を考えることにより、特異的な形状(窪みや尖り)やトポロジーの変化(上の動画で見たような穴の生成など)に自然に対応できる強力な手法である。物体の外側に初期閉曲線を設定し内側に曲面を収縮させるだけでなく、最初の動画で見たように、物体の内側に初期閉曲線を設定し外側に曲面を膨張させることもできる。
(赤線)である。Level Set法は、対象とする空間(今の場合2次元)より1次元高い空間(今の場合3次元)内の曲面を考えることにより、特異的な形状(窪みや尖り)やトポロジーの変化(上の動画で見たような穴の生成など)に自然に対応できる強力な手法である。物体の外側に初期閉曲線を設定し内側に曲面を収縮させるだけでなく、最初の動画で見たように、物体の内側に初期閉曲線を設定し外側に曲面を膨張させることもできる。
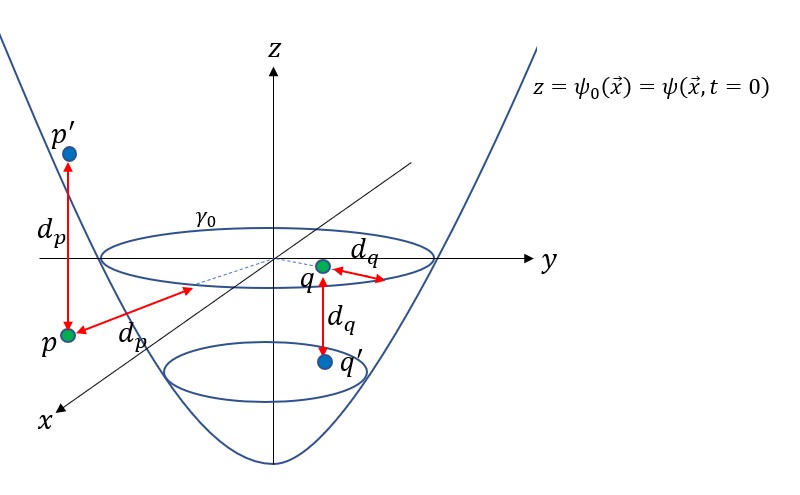
初期閉曲線![]() から曲面を作る手順は以下の通りである。
から曲面を作る手順は以下の通りである。![]() 平面上の点
平面上の点![]() を考える(右図の緑丸)。点
を考える(右図の緑丸)。点![]() は閉曲線
は閉曲線![]() の外側に、
の外側に、![]() は閉曲線の内側にある。それぞれの点から閉曲線までの距離を
は閉曲線の内側にある。それぞれの点から閉曲線までの距離を![]() とする。
とする。![]() を上側に
を上側に![]() だけ動かし点
だけ動かし点![]() を作る(青丸)。一方、
を作る(青丸)。一方、![]() に対しては下側に
に対しては下側に![]() だけ動かし点
だけ動かし点![]() を作る(青丸)。
を作る(青丸)。![]() 平面内の全ての点に対し同じことを繰り返すと(閉曲線の外側の点は上に動かし内側の点は下に動かす)初期閉曲線
平面内の全ての点に対し同じことを繰り返すと(閉曲線の外側の点は上に動かし内側の点は下に動かす)初期閉曲線![]() から曲面
から曲面![]() を作ることができる。ここで時間を変数に持つ曲面
を作ることができる。ここで時間を変数に持つ曲面
![]()
を考え、![]() と考える。曲面と
と考える。曲面と![]() 平面の交線を
平面の交線を![]() と書くことにすれば
と書くことにすれば
![]()
と書くことができ、![]() となる。以上で曲面の初期状態が定義された。次に曲面の時間発展を考える。
となる。以上で曲面の初期状態が定義された。次に曲面の時間発展を考える。![]() 平面上では
平面上では![]() を満たす。この両辺を
を満たす。この両辺を![]() で偏微分する。
で偏微分する。
![]()
![]() はあらわに
はあらわに![]() に依存する部分と
に依存する部分と![]() を通して
を通して![]() に依存する部分とを持つことに注意する。速度
に依存する部分とを持つことに注意する。速度![]() を使うと
を使うと
![]()
を得る。ただし、![]() とした。ここで
とした。ここで
![]()
(1) ![]()
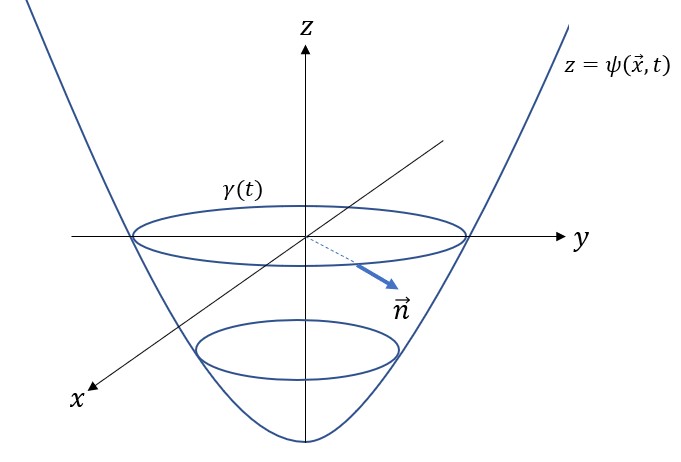
となる。![]() は閉曲線の法線ベクトルである(下図参照)。接線の向きと直交し外側へ向かうベクトルである。
は閉曲線の法線ベクトルである(下図参照)。接線の向きと直交し外側へ向かうベクトルである。
いま、![]() は法線に平行な方向に時間発展すると仮定すると
は法線に平行な方向に時間発展すると仮定すると
![]()
と書くことができる。ここで、![]() は速度の大きさを表す関数(速度関数)であり、閉曲線の曲率
は速度の大きさを表す関数(速度関数)であり、閉曲線の曲率![]() に依存させる。これを使うと式(1)は
に依存させる。これを使うと式(1)は
(2) ![]()
となる。この式が![]() の時間発展を記述する偏微分方程式である。これを初期条件
の時間発展を記述する偏微分方程式である。これを初期条件![]() の下で解く。時間発展が終了(速度が0)した時点の曲面と
の下で解く。時間発展が終了(速度が0)した時点の曲面と![]() 平面の交線が求めるべき閉曲線、すなわち物体の輪郭線となる。次に行うことは、
平面の交線が求めるべき閉曲線、すなわち物体の輪郭線となる。次に行うことは、![]() を具体的に定義し、式(2)を数値的に解くことができるよう差分方程式に変換するこであるが、難しい話になるので理論の話はこれで終わりにする。
を具体的に定義し、式(2)を数値的に解くことができるよう差分方程式に変換するこであるが、難しい話になるので理論の話はこれで終わりにする。
プログラム
10年ほど前にC++で実装したプログラムがここにある。この記事の冒頭に掲げた動画(画像に適用した例と3D物体に適用した例)も10年前に作成したものである。今回記事にするにあたりプログラムが動作することを確認した。
まとめ
Level Set法は1990年ころに提案された手法である。OpenCVもこれをサポートしているが、引数の意味が今一つ理解できないし、計算速度も遅い。そこで、昔の自作ライブラリを掘り出してきた。十分高速に精度良く動いていると思う。
参考文献
(1999).
Journal of Computational Physics, 118(2) 269-277 (1995).

