はじめに
機械学習は大きく2つに分けることができる。
- 教師あり学習:訓練データとして入力値と出力値がともに提供される場合
- 教師なし学習:訓練データとして入力値のみが与えられる場合
教師なし学習の1つであるK-meansクラスタリングは、データ解析業務において割と出番の多い手法である。今回は、K-meansクラスタリングの理論的説明を行い、画像処理に適用した実装例を示す。
理論
K-meansクラスタリングとは、あるデータの分布とクラスタ数![]() が与えられたとき、データ間の距離を基準にしてデータを
が与えられたとき、データ間の距離を基準にしてデータを![]() 個のクラスタに分割する処理である(下図は
個のクラスタに分割する処理である(下図は![]() のときの例)。
のときの例)。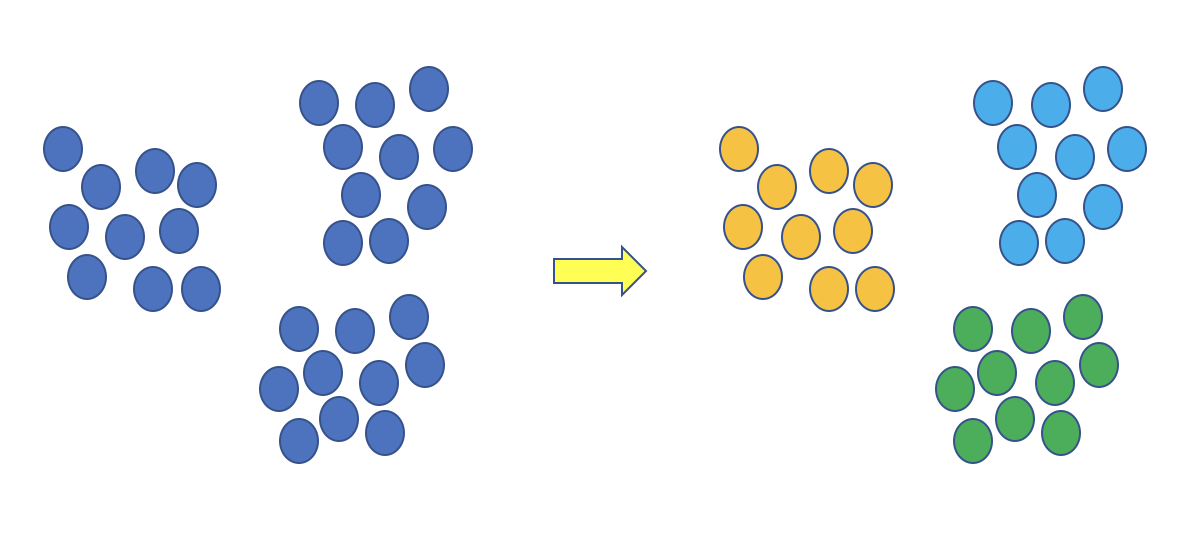
いま、![]() 次元ユークリッド空間内の点
次元ユークリッド空間内の点![]() を考える。
を考える。
(1) ![]()
![]() 個の点
個の点![]() が与えられたとき、これらを
が与えられたとき、これらを![]() 個のクラスタに分割することを考える。各クラスタの中心座標を
個のクラスタに分割することを考える。各クラスタの中心座標を![]() としたとき、最小にすべき目的関数
としたとき、最小にすべき目的関数![]() を次式で定義する。
を次式で定義する。
(2) 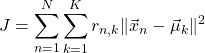
ここで、![]() は、点
は、点![]() がクラスタ
がクラスタ![]() に属するなら1を、そうでなければ0をとる変数である。
に属するなら1を、そうでなければ0をとる変数である。![]() を最小にする手順は以下の通りである。
を最小にする手順は以下の通りである。
 に適当な初期値を与える。
に適当な初期値を与える。 を固定し、
を固定し、 について
について を最小にする。
を最小にする。 を固定し、
を固定し、 について
について を最小にする。
を最小にする。 と
と が収束するまで、2と3の手順を繰り返す。
が収束するまで、2と3の手順を繰り返す。
手順2を実現することは容易である。ある点![]() を考えたとき、それに最も近い
を考えたとき、それに最も近い![]() を検索すれば良い。一方、手順3を実現するには、
を検索すれば良い。一方、手順3を実現するには、![]() を
を![]() で偏微分する(
で偏微分する(![]() の成分を
の成分を![]() とした)。
とした)。
(3) 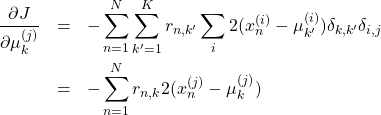
故に、
(4) 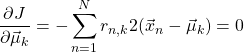
を得る。これより
(5) 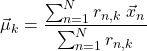
を得る。上式の分母はクラスタ![]() に属する点の総数である。すなわち、
に属する点の総数である。すなわち、![]() は、クラスタ
は、クラスタ![]() に属する点の重心となる。ここまでの議論を踏まえて、
に属する点の重心となる。ここまでの議論を踏まえて、![]() を最小にする手順を書き直すと以下のようになる。
を最小にする手順を書き直すと以下のようになる。
- クラスタの中心に適当な初期値を与える。
- 各点を一番近いクラスタに割り振る。
- 割り振られた点の重心を計算し、それを新たなクラスタの中心座標とする。
- クラスタの中心座標が変化しなくなるまで、2と3の手順を繰り返す。
実装
ここでは、K-meansクラスリングを画像処理に適用した例を示す。
最初に一枚のRGB画像を考える。各画素にはRGB値が割り当てられている。これを3次元ベクトルとみなすと一枚のRGB画像はRGB空間内の点の集合とみることできる。この空間内では、類似色同士が塊を作って分布しているはずである。この分布の偏りをK-meansクラスリングにより明確に分割してみる。使用するライブラリはOpenCV、言語はC++である。動作確認した環境は以下の通り。
- macOS Sierra
- Xcode(C++ Language Dialect: C++14)
- OpenCV-3.2.0
- boost-1.59.0
OpenCVのcv::kmeansを呼び出すだけである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 |
// // main.cpp // k_means_clustering // // Created by 熊田聖也 on 2017/10/19. // Copyright © 2017年 熊田聖也. All rights reserved. // #include <opencv2/opencv.hpp> #include <boost/range/adaptor/transformed.hpp> #include <boost/range/iterator.hpp> #include <boost/range/algorithm/copy.hpp> #include <boost/format.hpp> void show_result(const cv::Mat& labels, const cv::Mat& centers, int cluster_numger, int height, int width); int main(int argc, const char * argv[]) { // 最初の引数を見て、画像を読み込む auto image = cv::imread(argv[1]); if (image.empty()) { std::cout << "unable to load an input image\n"; return 1; } std::cout << "image: (" << image.rows << "," << image.cols << ")" << std::endl; // RGB画像であることを確認する。 if (image.type() != CV_8UC3) { std::cout << "non-color image\n"; } /* cv::kmeansは、各行に点の座標を持つ行列を要求する。したがって、入力画像を保持する行列imageの形状を (H*W, 3)に変更する。 */ auto reshaped_image = image.reshape(1, image.rows * image.cols); assert(reshaped_image.type() == CV_8UC1); std::cout << "reshaped_image: (" << reshaped_image.rows << ", " << reshaped_image.cols << ")" << std::endl; /* cv::kmeansは浮動小数点の行列を要求するので、型を変更する。同時に255で規格化しておく。 */ cv::Mat reshaped_image32f {}; reshaped_image.convertTo(reshaped_image32f, CV_32FC1, 1.0/255.0); assert(reshaped_image32f.type() == CV_32FC1); // クラスタ数を引数から取り出す。 const int cluster_number {atoi(argv[2])}; // 出力値を初期化する。 cv::Mat labels {}; cv::Mat centers {}; /* K-meansクラスタリングを停止させる条件を表現したクラスcv::TermCriteriaのインスタンスを 作成する。今回は最大繰り返し数を100とした。最後の引数の1はここではダミーである。 */ cv::TermCriteria criteria {cv::TermCriteria::COUNT, 100, 1}; /* K-meansクラスタリングを実行する。 cv::kmeansの第6引数にcv::KMEANS_RANDOM_CENTERSを指定した。これは、クラスタの中心座標の初期値を乱数で 決めることを意味する。 */ cv::kmeans(reshaped_image32f, cluster_number, labels, criteria, 1, cv::KMEANS_RANDOM_CENTERS, centers); // 結果を表示する。 show_result(labels, centers, cluster_number, image.rows, image.cols); return 0; } void show_result(const cv::Mat& labels, const cv::Mat& centers, int cluster_number, int height, int width) { /* 画像の形状を(H,W)とすると、labelsの形状は(H*W,1)である。各行にはラベルの値が整数値で収められている。 cluster_numberを3とすれば、0,1,2のいずれかとなる。 centersの形状は(cluster_numeber,3)である。各行にクラスタの中心座標が収められている。今の場合、(B,G,R)の 値が並ぶことになる。 */ std::cout << "labels: " << "(" << labels.rows << ", " << labels.cols << ")" << std::endl; std::cout << "centers: " << "(" << centers.rows << ", " << centers.cols << ")" << std::endl; assert(labels.type() == CV_32SC1); assert(centers.type() == CV_32FC1); /* centersの要素の型は浮動小数点である。これを0から255までのstd::uint8_tの型に変更する。 さらに、チャンネル数を3に変更する。 */ cv::Mat centers_u8 {}; centers.convertTo(centers_u8, CV_8UC1, 255.0); const auto centers_u8c3 = centers_u8.reshape(3); assert(centers_u8c3.type() == CV_8UC3); // K-meansクラスタリングの結果を画像に変換して表示するので、入れ物を初期化する。 cv::Mat rgb_image {height, width, CV_8UC3}; /* 画像に変換する。 1. labelsからひとつずつ値を取り出す。 2. そのラベルに相当するRGB値を取り出して、rgb_imageへコピーする。 cv::Matの要素へのアクセスは下記のようにポインタを使うのが最速である。 */ boost::copy( boost::make_iterator_range(labels.begin<int>(), labels.end<int>()) | boost::adaptors::transformed([¢ers_u8c3](const auto& label){ return *centers_u8c3.ptr<cv::Vec3b>(label); }), rgb_image.begin<cv::Vec3b>() ); // 表示する。 cv::imshow("result", rgb_image); // 出力パスを作り、保存する。 const auto output_path = (boost::format("%1%_result.jpg") % cluster_number).str(); cv::imwrite(output_path, rgb_image); cv::waitKey(); } |
実行コードは以下の通り。
|
1 |
$> ./k_means_clustering sample.jpeg 20 |
最初の引数は画像へのパス、2番目の引数はクラスタ数を表す。さまざまなクラスタ数の時の結果を以下に示す。各クラスタの色はそのクラスタの重心座標の色である。
![]()

![]()

![]()

![]()

![]()

![]()

元画像
いわゆる減色処理が行われていることになる。
まとめ
今回はデータ解析においてしばしば用いられるK-meansクラスタリングを説明し、画像処理に適用した例を示した。画像は、見方を変えれば、グリッド上に並ぶ3次元ベクトルの集合である。K-meansクラスタリングにより、少ない数の色(カラーパレット)で画像を表現することができる。
ところで、上記のboost::copyの中身は理解できたでしょうか?

