はじめに
今回は補間を説明し、それを応用した画像処理(拡大・縮小)について説明する。目次は以下の通り。
線形(Linear)補間
最初に1次元の線形補間を考える。2次元空間内に曲線![]() が存在し、
が存在し、![]() が
が![]() の時の
の時の![]() の値
の値![]() が既知であるとする。このとき
が既知であるとする。このとき![]() を見たす
を見たす![]() に対応する
に対応する![]() の値を求めたい(下図参照)。
の値を求めたい(下図参照)。
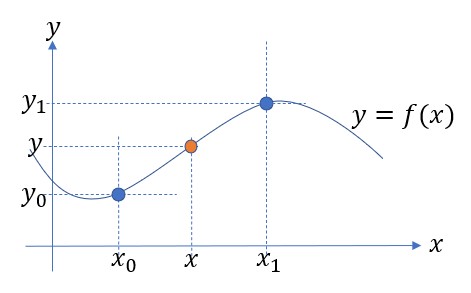
線形補間では、領域内(![]() )の曲線を次式で近似する。
)の曲線を次式で近似する。
(1) 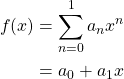
(2) ![]()
したがって
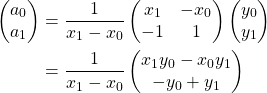
を得る。これらの値を式(1)に代入すると
![]()
を得る。この式は傾き![]() を持つ
を持つ![]() を通る直線であり、わざわざ行列を持ち出して解くまでもない。しかし、このあと説明する補間の式変形と統一するため行列を用いた。
を通る直線であり、わざわざ行列を持ち出して解くまでもない。しかし、このあと説明する補間の式変形と統一するため行列を用いた。
双線形(Bilinear)補間
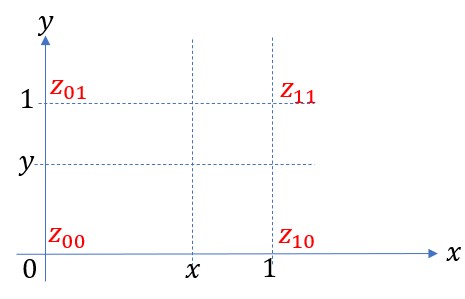
次に上の線形補間を曲面に拡張する(下図参照)。
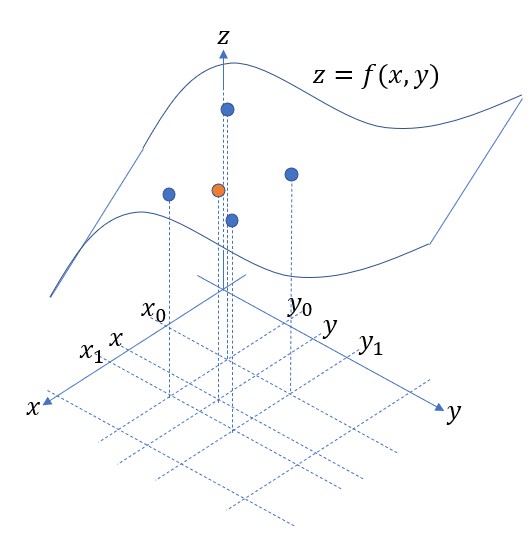
既知の値は![]() 上の値
上の値![]() である。曲面の近似式を次式で与える。
である。曲面の近似式を次式で与える。
(3) 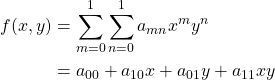
4つの式
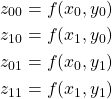
(4) 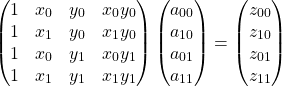
を得る。これを解けば![]() を求めることができる。このまま解くのは面倒なので
を求めることができる。このまま解くのは面倒なので![]() として解いてみる。このとき式(4)は
として解いてみる。このとき式(4)は

となる。この式は掃き出し法(覚えてますか?)を使えば容易に解くことができる。
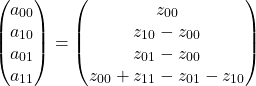
これらを式(3)に代入し整理すると
(5) ![]()
を得る。この式は![]() 軸上の比と
軸上の比と![]() 軸上の比から補間することを表している。(下図参照)。
軸上の比から補間することを表している。(下図参照)。
Cubic補間
ここまでは線形補間を考えてきた。次に3次式の補間を考える。まず最初に1次元の場合である(下図参照)。
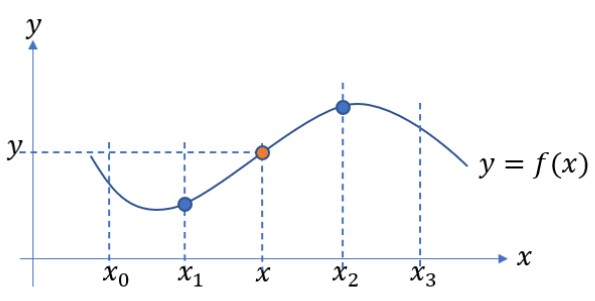
補間したい点![]() の両隣に2つずつ既知の点
の両隣に2つずつ既知の点![]() を取る。それぞれに対する
を取る。それぞれに対する![]() の値も既知である(
の値も既知である(![]() )。近似式として次を考える。
)。近似式として次を考える。
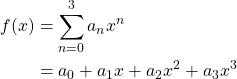
(6) 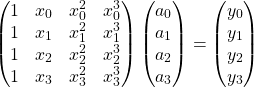
を得る。これを![]() について解けば良い。式(2)や式(6)の左辺に現れる行列は線形代数ではヴァンデルモンド行列と呼ばれる。
について解けば良い。式(2)や式(6)の左辺に現れる行列は線形代数ではヴァンデルモンド行列と呼ばれる。
Bicubic補間
最後に、Cubic補間を曲面の場合に拡張する(下図参照)。
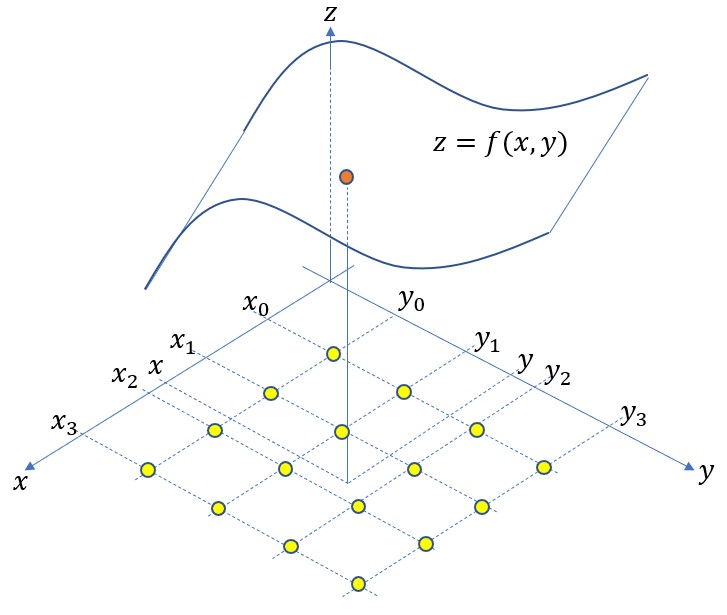
既知の点は図の黄色の座標上にある16個の点である(![]() )。この時の近似式は
)。この時の近似式は
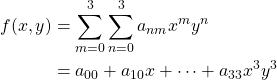
である。これまでと同じことを繰り返せば、16個の式から16行16列の行列で記述される連立方程式を作ることができる。ここまでくると方程式を書き下ろすのもさすがに憚られる。
画像処理への応用
上で説明したBilinear補間とBicubic補間は画像処理における拡大・縮小に使われている。拡大・縮小の手順は以下の通りである(下図参照)。
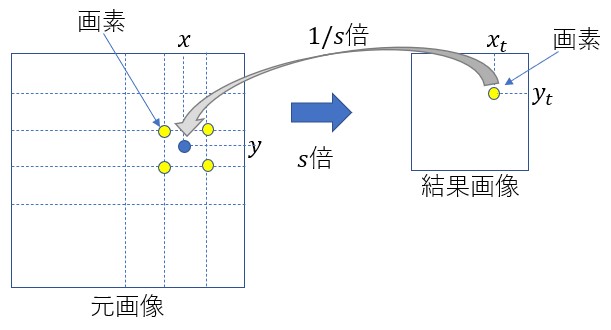
補間を行う際、画像を3次元空間内の曲面であると考えていることに注意する(下図参照)。
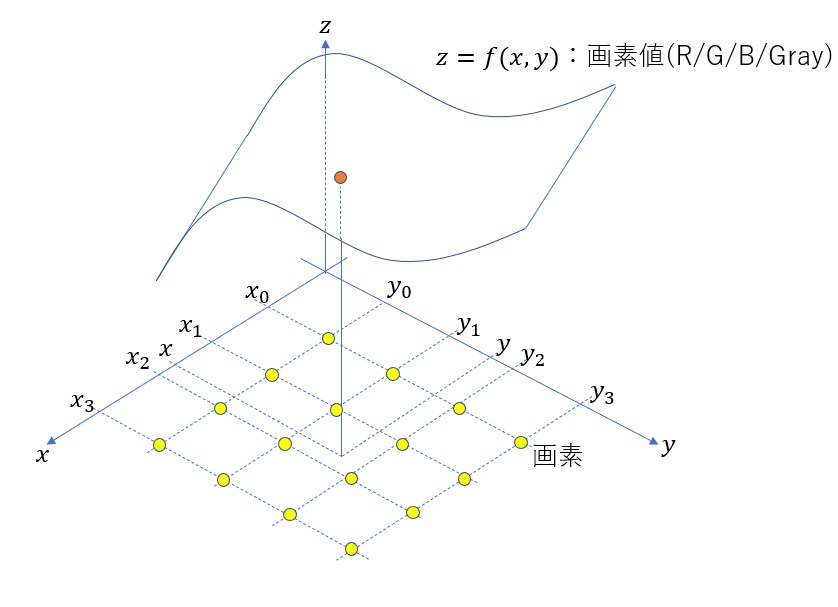
実装
Bicubic補間は大変なので、Bilinear補間をRustで実装する。式(5)を使うことができる(以下に再掲した)。
![]()
すなわち、補間したい座標を囲む4つの画素を使い、![]() 軸に沿う比
軸に沿う比![]() と
と![]() 軸に沿う比
軸に沿う比![]() を用いて計算すれば良い。ソースコードはここ。ソースの一部は以下の通り。
を用いて計算すれば良い。ソースコードはここ。ソースの一部は以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// Bilinear補間 pub fn resize_with_bilinear(src: &image::Rgb32FImage, scale: f32) -> image::RgbImage { let (src_w, src_h) = src.dimensions(); let dst_w = (src_w as f32 * scale) as u32; let dst_h = (src_h as f32 * scale) as u32; let mut dst = image::RgbImage::new(dst_w, dst_h); for j in 0..dst_h { let fy = j as f32 / scale; // 元画像における位置を計算(不動小数点) let mut y0 = fy as u32; y0 = cap(y0, src_h); let y = fy - (y0 as f32); let mut y1 = y0 + 1; y1 = cap(y1, src_h); for i in 0..dst_w { let fx = i as f32 / scale; // 元画像における位置を計算(不動小数点) let mut x0 = fx as u32; x0 = cap(x0, src_w); let x = fx - x0 as f32; let mut x1 = x0 + 1; x1 = cap(x1, src_w); let dp = make_color_by_bilinear(y0, y1, x0, x1, y, x, src); dst.put_pixel(i, j, dp); } } return dst; } |
呼び出し元は以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
fn main() { let image_path = "c:/Users/seiya.kumada/Pictures/firefox_logo.png"; let scale = 2.1; let img = image::open(image_path).unwrap().to_rgb8(); let dst = imgproc::resize_with_nearest_neighbor(&img, scale); dst.save("./outputs/nearest.jpg").unwrap(); let img = image::open(image_path).unwrap().to_rgb32f(); let dst = imgproc::resize_with_bilinear(&img, scale); dst.save("./outputs/bilinear.jpg").unwrap(); } |
Rustには画像を扱うためのcrate「image」があるのでこれを利用する。Bilinear補間で浮動小数点を扱いたいので画像を読み込む際に画素値を[0,1]の範囲の浮動小数点に変換している(10行目)。また、補間したい画素値を最近傍の画素値に置き換える処理も合わせて実装した(最近傍補間)。倍率![]() のときの結果は以下の通り。
のときの結果は以下の通り。

Bilinear補間の方が色の境界線におけるギザギザが抑制されていることが分かる(アンチエイリアスが効いている)。
まとめ
今回はいくつかの補間方法を紹介し、その中の一つを画像処理に応用した例を示した。

