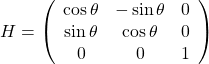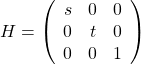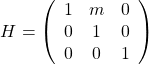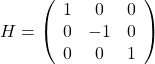はじめに
今回は、Affine変換とHomography変換について説明する。
Affine変換
(1) ![]()
ここで
(2) 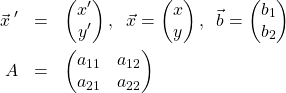
である。これらを代入して、成分で書き直すと
(3) ![]()
(4) 
上の行列は6個のパラメータを持つ。これらを一意に決めるには既知の点の組み![]() が3つあれば良い。これら3組みから決まる変換(1)をAffine変換と呼ぶ。ところで、式(4)は次式のように書くこともできる。
が3つあれば良い。これら3組みから決まる変換(1)をAffine変換と呼ぶ。ところで、式(4)は次式のように書くこともできる。
(5) 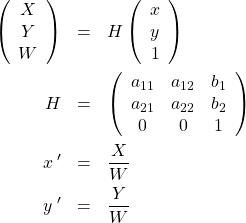
これを同次座標表現と呼ぶ。考えている空間を1次元足した空間に拡張することで行列を正方行列とすることができ、式変形が容易になる。
式(5)で記述できる変換は以下の通りである。
- 回転:例えば、
 回転の変換は
回転の変換は
(6)

で実現できる。
- 縮小・拡大:例えば、
 軸方向に
軸方向に 倍、
倍、 軸方向に
軸方向に 倍する変換は
倍する変換は
(7)

で実現できる。
- 平行移動:例えば、
 軸方向に
軸方向に 、
、 軸方向に
軸方向に だけ移動する変換は
だけ移動する変換は
(8)

で実現できる。
- せん断:例えば、水平方向のせん断は
(9)

で実現できる。
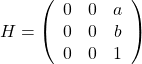
- 反転:例えば、
 軸についての反転は
軸についての反転は
(10)

で実現できる。
これらを組み合わせた変換は、行列の掛け算をすれば良い。上の実例から分かる通り、平行な辺の組みは平行なまま変換されるのがAffine変換である。
Homography変換
変換(5)を拡張して
(11) 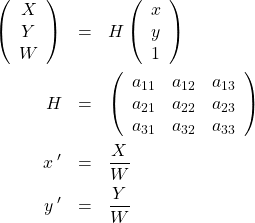
を考える。パラメータの数は9である。ここで、行列の全要素に同じ数![]() をかけた変換を考える。このとき変換後のベクトルは
をかけた変換を考える。このとき変換後のベクトルは
(12) 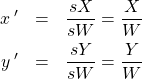
となる。すなわち、式(11)の変換には定数倍だけの不定性がある。この不定性を取り除くため全要素を、例えば![]() で割り、改めて成分を書き直す。
で割り、改めて成分を書き直す。
(13) 
パラメータ数は8となるので、既知の点の組みが4つあれば上の行列を一意に決めることができる。変換(11)をHomography変換と呼ぶ。Homography変換は、Affine変換で実現できる全ての変換だけでなく、平行な辺の組みを平行でない辺の組みに変換することもできる。例えば
(14) 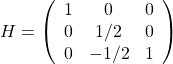
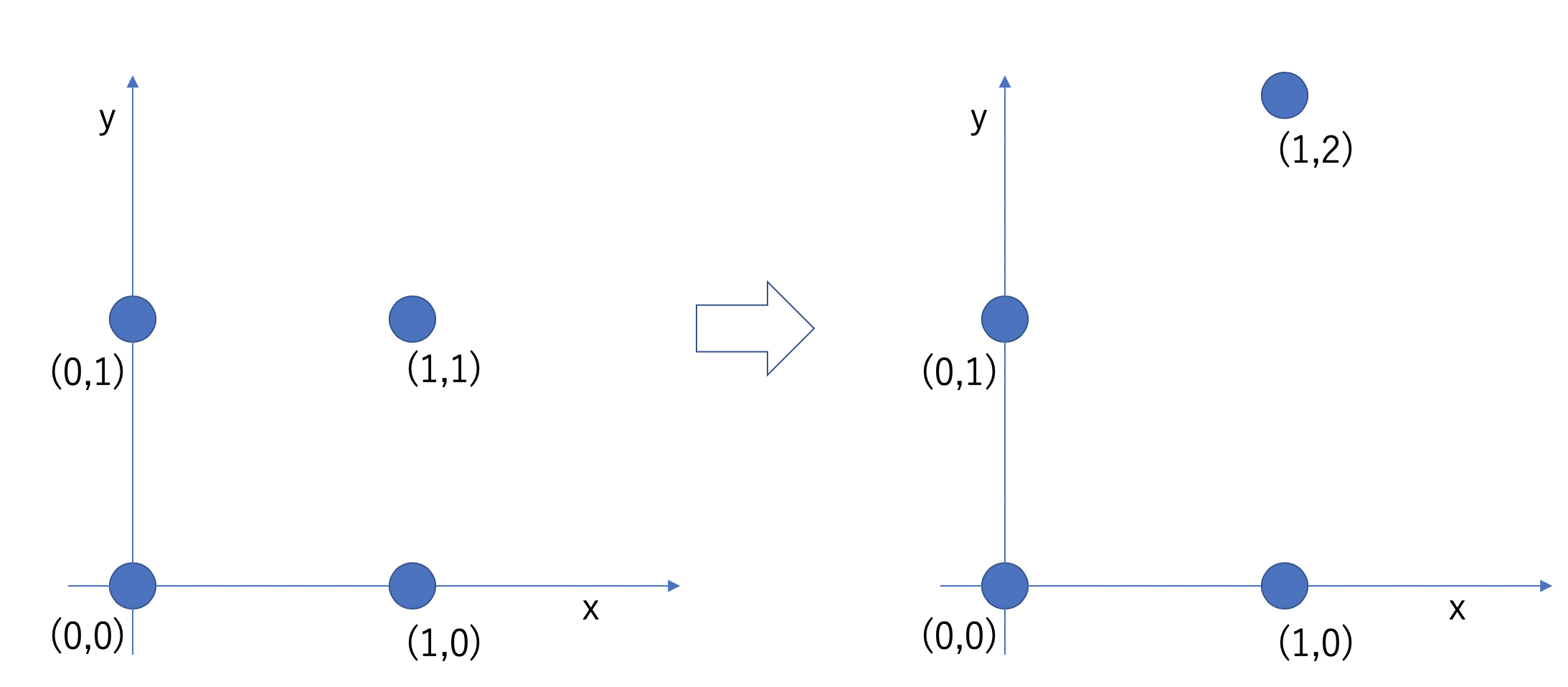
は、(0,0),(1,0),(1,1),(0,1)を頂点とする長方形を、(0,0),(1,0),(1,2),(0,1)を頂点とする台形に変換することができる(下図参照)。
OpenCVのコード
OpenCVを用いたHomography変換のサンプルコードを以下に示す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#include #include #include #include const std::string PATH = std::string("/Users/kumada/Documents/Orizuruブログ/homography/himawari.jpeg"); int main(int argc, const char * argv[]) { const cv::Mat src = cv::imread(PATH); const auto src_size = src.size(); const auto width = src_size.width; const auto height = src_size.height; std::cout << "(width, height) = (" << width << ", " << height << ")" << std::endl; cv::Mat dst= cv::Mat::zeros(height + 5, width + 5, CV_8UC3); // 変換前の画像での座標 const std::vector src_pt = { cv::Point2f(41, 4), cv::Point2f(187, 21), cv::Point2f(43, 216), cv::Point2f(189, 203) }; // 変換後の画像での座標 const std::vector dst_pt = { cv::Point2f(14, 4), cv::Point2f(14 + 198, 4), cv::Point2f(14, 4 + 217), cv::Point2f(14 + 198, 4 + 217) }; // homography行列を計算 const cv::Mat homography_matrix = getPerspectiveTransform(src_pt, dst_pt); // 行列を入力画像に演算 warpPerspective(src, dst, homography_matrix, dst.size()); cv::imshow("result", dst); cv::imwrite("/Users/kumada/Documents/Orizuruブログ/homography/out.jpg", dst); cv::waitKey(); return 0; } |
適用結果は以下の通り。

左側の額縁の頂点①②③④が右側の額縁の頂点①②③④となるように変換した例である。
まとめ
今回は、Affine変換と、それを拡張したHomography変換を紹介した。ここでは、Homography変換のOpenCVによる実装例だけを示したが、Affine変換も同様に実装できる。OpenCVを使えば、メジャーなアルゴリズムを理論的背景を知ることなく使うことができるが、時には立ち止まって背景を見ることも必要である。