はじめに
今回は、混合ガウスモデルと、そのパラメータを求める際に使われる最尤推定法についてまとめる。そのあと、OpenCVを用いたコード例を示す。
混合ガウスモデル
ある確率分布![]() が与えられとき、これをガウス関数の線形結合で近似することを考える。
が与えられとき、これをガウス関数の線形結合で近似することを考える。
(1) 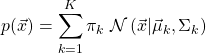
ここで、![]() は、平均値
は、平均値![]() 、共分散
、共分散![]() を持つガウス関数(正規分布)である。
を持つガウス関数(正規分布)である。![]() は各ガウス関数の重みを表す。このように、任意の分布をガウス関数の線形結合で近似することを混合ガウスモデルと呼ぶ。上式の両辺を
は各ガウス関数の重みを表す。このように、任意の分布をガウス関数の線形結合で近似することを混合ガウスモデルと呼ぶ。上式の両辺を![]() で積分すると次式を得る。
で積分すると次式を得る。
(2) 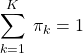
ここで、ガウス関数は規格化されていることを用いた。この式は![]() に課せられる拘束条件である。
に課せられる拘束条件である。
いま、観測点の集合![]() を考える。これらが同時に実現する確率
を考える。これらが同時に実現する確率![]() は、独立同一分布を仮定すれば、以下のように書くことができる。
は、独立同一分布を仮定すれば、以下のように書くことができる。
(3) 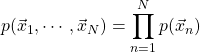
式(1)を代入すると
(4) 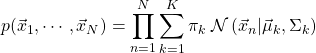
を得る。右辺に存在する全パラメータ![]() を決定し、出来るだけ正確に左辺値(観測結果)を再現することを考える。つまり、どのパラメータを選べば観測値を尤もらしく再現できるかという問題を考えることになる。この文脈に於いて、式(3)は尤度と呼ばれる。
を決定し、出来るだけ正確に左辺値(観測結果)を再現することを考える。つまり、どのパラメータを選べば観測値を尤もらしく再現できるかという問題を考えることになる。この文脈に於いて、式(3)は尤度と呼ばれる。
最尤推定法
「観測値を尤もらしく再現する」とは、同時確率分布を最大にすることである。ただし、計算の便宜上、次の尤度の対数(対数尤度)を最大化する。
(5) 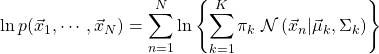
(対数)尤度を最大化することでパラメータを決定する手法を最尤推定法と呼ぶ。拘束条件(2)をLagrange乗数![]() を用いて取り込んだ次式を最大化する。
を用いて取り込んだ次式を最大化する。
(6) 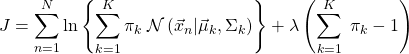
![]() を各パラメータで偏微分し、それぞれを0と置けば良い。
を各パラメータで偏微分し、それぞれを0と置けば良い。![]() による偏微分から次式を得る。
による偏微分から次式を得る。
(7) 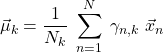
ここで、
(8) 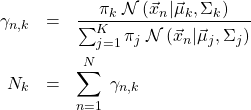
とした。![]() による偏微分から次式を得る。
による偏微分から次式を得る。
(9) 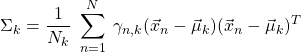
ここで![]() は転置を表す。最後に、
は転置を表す。最後に、![]() による偏微分から
による偏微分から
(10) ![]()
を得る。パラメータ![]() が、全て
が、全て![]() で表されていることに注意する。つまり、
で表されていることに注意する。つまり、![]() が求まれば、
が求まれば、![]() は全て求まる。しかし、
は全て求まる。しかし、![]() を求めるには、
を求めるには、![]() が決まらなければならない。これを解く1つの手法が以下に示す反復法である。
が決まらなければならない。これを解く1つの手法が以下に示す反復法である。
 を適当な値で初期化する。
を適当な値で初期化する。 を計算する。
を計算する。 を用いて、
を用いて、 を計算する。
を計算する。 を用いて、式(5)を計算する。
を用いて、式(5)を計算する。 が収束するまで、あるいは、式(5)が収束するまで、手順2から4までを繰り返す。
が収束するまで、あるいは、式(5)が収束するまで、手順2から4までを繰り返す。
手順1に於いて、![]() の初期値を求める際、K-meansクラスタリングがしばしば用いられる。
の初期値を求める際、K-meansクラスタリングがしばしば用いられる。![]() 個のクラスタの中心座標を、
個のクラスタの中心座標を、![]() と見なせば良い。
と見なせば良い。
ところで、![]() は次式で与えられた。
は次式で与えられた。
(11) ![]()
この式は、点![]() が与えられたとき、その点がどのガウス関数に属しているかを表す事後確率
が与えられたとき、その点がどのガウス関数に属しているかを表す事後確率![]() を表す。両辺を
を表す。両辺を![]() で和を取ると、次式が成り立つことに注意する。
で和を取ると、次式が成り立つことに注意する。
(12) 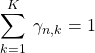
詳細は省くが、上に示した反復法は、混合ガウスモデルにEMアルゴリズムと呼ばれる手法を適用した場合の手順と、厳密に等価であることが示される。
実装
混合ガウスモデルにEMアルゴリズムを適用するプログラムを以下に示す。言語はC++、ライブラリはOpenCVである。対象はRGB画像である。画像上の各画素値(3次元ベクトル)が観測値に相当する。すなわち、![]() である。
である。![]() は全画素数である。RGB空間に存在する観測点の分布を混合ガウスモデルで再現しようとする試みである。最初に全プログラムを示す。
は全画素数である。RGB空間に存在する観測点の分布を混合ガウスモデルで再現しようとする試みである。最初に全プログラムを示す。
- macOS Sierra
- Xcode Version 9.2(C++ Language Dialect: C++17)
- OpenCV-3.2.0
- boost-1.65.1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 |
#include <opencv2/opencv.hpp> #include <numeric> #include <boost/range/adaptor/transformed.hpp> #include <boost/range/algorithm/copy.hpp> #include <boost/range/irange.hpp> #include <boost/range/algorithm/for_each.hpp> #include <boost/format.hpp> #include <fstream> constexpr int DIMENSION {3}; constexpr int CLUSTER_NUM {10}; constexpr double EPSILON {1.0e-08}; // 各画素にCLUSTER_NUM個の値が割り振られている。 // これらはどのクラスタに属するかを決める確率であるから和は1である。 void observe_probs(const cv::Mat& probs) { const auto range = boost::irange(0, probs.rows); boost::for_each(range, [&probs](const auto& n){ const auto gamma_n = probs.ptr<double>(n); if (auto total = std::accumulate(gamma_n, gamma_n + CLUSTER_NUM, 0.0); std::abs(total - 1.0) >= EPSILON) { std::cout << "ERROR\n"; } }); } // 重みの和は1である。 void observe_weights(const cv::Mat& weights) { if (auto total = std::accumulate(weights.begin<double>(), weights.end<double>(), 0.0); std::abs(total - 1.0) >= EPSILON) { std::cout << "ERROR\n"; } } void save_means(const cv::Mat& means) { auto path = boost::format("/Users/kumada/Projects/cct_blog/em_algorithm/means_%1%.txt") % CLUSTER_NUM; auto fout = std::ofstream(path.str()); const auto range = boost::irange(0, means.rows); boost::for_each(range, [&means, &fout](const auto& i){ const auto ptr = means.ptr<cv::Vec3b>(i); fout << *ptr << std::endl; }); } void observe_labels_and_means(const cv::Mat& labels, const cv::Mat& means, int height, int width) { // 新規の画像(出力) cv::Mat rgb_image(height, width, CV_8UC3); // 浮動小数点数をuint_8に、チャンネル数を3に変換する。 cv::Mat means_u8 {}; means.convertTo(means_u8, CV_8UC1, 255.0); cv::Mat means_u8c3 = means_u8.reshape(DIMENSION); save_means(means_u8c3); boost::copy( boost::make_iterator_range(labels.begin<int>(), labels.end<int>()) | boost::adaptors::transformed( [&means_u8c3](const auto& label){ return *means_u8c3.ptr<cv::Vec3b>(label); } ), rgb_image.begin<cv::Vec3b>() ); cv::imshow("tmp", rgb_image); auto path = boost::format("/Users/kumada/Projects/cct_blog/em_algorithm/em_result_%1%.jpg") % CLUSTER_NUM; cv::imwrite(path.str(), rgb_image); cv::waitKey(); } void save_labels(const cv::Mat& labels) { auto path = boost::format("/Users/kumada/Projects/cct_blog/em_algorithm/labels_%1%.txt") % CLUSTER_NUM; auto fout = std::ofstream(path.str()); const auto range = boost::irange(0, labels.rows); boost::for_each(range, [&labels, &fout](const auto& i){ const auto ptr = labels.ptr<int>(i); fout << *ptr << std::endl; }); } int main(int argc, const char * argv[]) { // 画像を読み込む。 auto image = cv::imread(argv[1]); assert(image.type() == CV_8UC3); std::cout << image.rows << ", " << image.cols << std::endl; const auto image_rows = image.rows; const auto image_cols = image.cols; // 形状を変える。 auto reshaped_image = image.reshape(1, image_rows * image_cols); assert(reshaped_image.type() == CV_8UC1); // 行数は画素数、列数は3である。 assert(reshaped_image.rows == image_rows * image_cols); assert(reshaped_image.cols == DIMENSION); // EMアルゴリズムの入力を作る。 cv::Mat samples {}; reshaped_image.convertTo(samples, CV_64FC1, 1.0 / 255.0); assert(samples.type() == CV_64FC1); assert(samples.rows == image_rows * image_cols); assert(samples.cols == DIMENSION); std::cout << samples.at<cv::Vec3d>(21*81) << std::endl; // EMアルゴリズムを初期化する。 auto model = cv::ml::EM::create(); // ガウス関数の個数(Kに相当する) model->setClustersNumber(CLUSTER_NUM); // 共分散行列として正の値を持つ対角行列を仮定する。 model->setCovarianceMatrixType(cv::ml::EM::Types::COV_MAT_DIAGONAL); // 出力を用意する。 cv::Mat labels {}; cv::Mat probs {}; cv::Mat log_likelihoods {}; // 実行する。 // 初期値はK-meansクラスタリングにより決まる。 model->trainEM(samples, log_likelihoods, labels, probs); // 出力を確認する。各画素の対数尤度の値 assert(log_likelihoods.type() == CV_64FC1); assert(log_likelihoods.rows == image_rows * image_cols); assert(log_likelihoods.cols == 1); // 出力を確認する。各画素に割り振られたラベルの値 assert(labels.type() == CV_32SC1); assert(labels.rows == image_rows * image_cols); assert(labels.cols == 1); save_labels(labels); // 出力を確認する。各画素に割り振られた事後確率の値 assert(probs.type() == CV_64FC1); assert(probs.rows == image_rows * image_cols); assert(probs.cols == CLUSTER_NUM); observe_probs(probs); // 出力を確認する。各ガウス関数の平均値 const auto& means = model->getMeans(); assert(means.type() == CV_64FC1); assert(means.rows == CLUSTER_NUM); assert(means.cols == DIMENSION); observe_labels_and_means(labels, means, image_rows, image_cols); // 出力を確認する。各ガウス関数の重み const cv::Mat& weights = model->getWeights(); assert(weights.type() == CV_64FC1); assert(weights.rows == 1); assert(weights.cols == CLUSTER_NUM); observe_weights(weights); return 0; } |
各処理と理論式とを対応づける。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// 各画素にCLUSTER_NUM個の値が割り振られている。 // これらはどのクラスタに属するかを決める確率であるから和は1である。 void observe_probs(const cv::Mat& probs) { const auto range = boost::irange(0, probs.rows); boost::for_each(range, [&probs](const auto& n){ const auto gamma_n = probs.ptr<double>(n); if (auto total = std::accumulate(gamma_n, gamma_n + CLUSTER_NUM, 0.0); std::abs(total - 1.0) >= EPSILON) { std::cout << "ERROR\n"; } }); } |
上記は
(13) 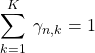
を確認している。
|
1 2 3 4 5 6 7 |
// 重みの和は1である。 void observe_weights(const cv::Mat& weights) { if (auto total = std::accumulate(weights.begin<double>(), weights.end<double>(), 0.0); std::abs(total - 1.0) >= EPSILON) { std::cout << "ERROR\n"; } } |
上記は
(14) 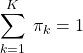
を確認している。また、log_likelihoodsは
(15) 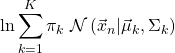
に対応し、labelsは
(16) ![]()
に対応し、meansは![]() に対応する。
に対応する。
結果
次のコマンドで実行する。実行ファイルに続けて画像パスを入力する。
|
1 |
gt; ./exe sample_2.jpeg |
計算結果を以下に示す。![]() は考慮するガウス関数の数である。
は考慮するガウス関数の数である。

RGB空間内の色の分布![]() を混合ガウスモデルで近似し、各画素の色を、labelsに対応するガウス関数の平均値
を混合ガウスモデルで近似し、各画素の色を、labelsに対応するガウス関数の平均値![]() に置き換えたものである。
に置き換えたものである。
まとめ
色分布を適当なグループに分離し、各画素をそのグループを代表する色で置き換えるという手順は、先に説明したK-meansクラスタリングと同じである。どちらが優れているかという議論は一概にはできない。ただし、今回の方が手順が複雑な分、計算時間は長いことだけを指摘しておく。
今回説明した反復法は、EMアルゴリズムの具体例である。一般的なEMアルゴリズムの説明は、例えば「Pattern Recognition and Machine Learning」を参照されたい。
本プログラムは2013年に書いたものをベースとした。今回再録するにあたり、OpenCVのインターフェース、C++のインタフェースを大幅に書き換えた。

