はじめに
こんにちは、エンジニアのせーさんです。
最近自社プロダクトの開発で 1~2 年目の若手に作業をお願いする事が多いのですが、 ロジカルシンキングの力に個人差、または、個人でも得意な部分、不得意な部分がある事に気付きました。
ということで、前回から大分経ってしまいましたが Vol.2 の「ロジカルシンキング編」になります。
- Vol.1 コミュニケーション編
- Vol.2 ロジカルシンキング編 (本記事)
- Vol.3 技術スキル基本編
では早速本編へどうぞ。
ロジカルシンキング編
ロジカルシンキング (= 論理的思考) というとブログや書籍などではよく目にするキーワードで
- MECE
- So What? Why So?
- ロジックツリー
みたいな考え方や、それらを元にしたフレームワークに関する説明や解説、応用方法が出てくると思います。
これらの考え方は「思考のフレームワークに共通の名前を付けて共有する」という意味で極めて重要なのですが、その手前にある「数学的な考え方」の基礎ができていないと本当の意味で使い方が分からないと思います。
これは個人的な見解ですが、冒頭に話したロジカルシンキングの力に関する「個人差」や「得意/不得意」の原因は「数学的な考え方」への理解度に依存していると感じています。
例えるのであれば「四則演算が正確にできない状態で連立方程式を解いてる。」イメージですね、それでは正しい答えは導き出せません。
義務教育のカリキュラムにこの「数学的な考え方」に特化した授業はなく(少なくとも私の時代は)、各個人が勉強する中、もしくは、日常生活や趣味活動の中などで自然と「数学的な考え方」を学ぶのですが、体系化されていないので人によって習熟度がまちまちな印象です。
1. 数学的な考え方とは
ではその「数学的な考え方」ってなんやねん?ってことになりますが、このあたりもキーワードさえ知っていればブログや書籍がたくさんあるジャンルかと思います。
詳細な説明はググってもらうとして、まずは抑えるべき 4 つのポイントを簡単にまとめました。
難しいイメージの漢字が並びますが、やりたいことはとても単純です!
- ものごとを正しく捉える/伝えるための考え方
- 事実と仮説
- 原理と原則
- 事実を重ねて理論/推論を展開するための考え方
- 三段論法 / 演繹(えんえき)法
- 帰納法
1-1. 事実と仮説
「仮説」の部分に関しては場合により「意見」などと言い換えてもいいと思います。
要は「確実にそうと言える内容」と「そうだと思うことや、推測、願望」を区別する、ということですね。
この 2 つを正しく区別できないと、積み上げた理論が土台から崩れてしまいます。
もちろん場合によっては「仮説であることを前提」に理論を展開することにより、「仮説」を検証した結果、「仮説」から「事実」に変わることもあります。
まずは「人に情報を伝える」「人から情報を受け取る」際に、「事実」と「仮説」を明確に区別しましょう。
そして、自分が何かを考えるときにも「事実」と「仮説」を整理しましょう。
割とこれが出来てない人は多い気がします。
例えば「上長に指示や判断を仰ぐために報告する場合、自分の意見や考えがごちゃまぜになっちゃう。」みたいな、あるあるですね。
1-2. 原理と原則
「原理原則に基づいて…」みたいにまとめて使われる事が多いですが、「原理」と「原則」は別の言葉です。
「原理」は変えようのない根本的は法則です。補足すると「少なくとも 2021 年現時点の科学において」みたいな適用範囲は必要ですが。
例えばこんなことでしょうか。
- 時間は過去から未来に向かって流れる
- モノは上から下に落ちる
- 人はいずれ死ぬ
「原則」は「原理」に比べて比較的変わる事が多い、集団(国、社会、地域、会社、組織)などでの共通的なルールや決まりごとです。
例えばこんな感じでしょうか。
- 犯罪行為を犯したら捕まる – 日本国内の法律というルール
- 遅刻する場合は事前に連絡 – 会社の就労規則というルール
要は「原則」と比較すると「変更される可能性がある」ものですね。
つまり抑えるべきは「いまの論理展開で適用される原理と原則が何なのか?」を忘れないということです。
「よそはよそ、うちはうち」みたいなお母さんがおもちゃを買ってくれないときの定番の理由も、家庭によって「原則」が異なるからですね!
1-3. 三段論法 / 演繹(えんえき)法
三段論法は「2 つ以上の前提から結論を導き出す手法」で、具体的にはこんなイメージです。
「A であり(1 段: 前提 1)、B であるならば(2 段: 前提 2)、C である。(3 段: 結論)」
数学の証明でやりましたね、これだけです。
でも社会に出ても実は使うんです。というか、めちゃめちゃ使います。
1-4. 帰納法
三段論法は「前提から結論を導き出す手法」ですが、帰納法は「複数の事実から共通項目を推測する」手法です。
三段論法と違って「〜っぽいよね」という推測をする手法なので、個人の背景に知識や経験により推測が変わります。
例えば「新サービスに追加する機能について意見を出し合おう!」のような、みんなで考える時に使います。
2. 押さえておきたいオススメの考え方
さて「数学的な考え方」の基本をお伝えしたところで、どんなときにも使えて個人的に最も重要視している考え方(フレームワーク)をお伝えしたいと思います。 それが「AsIs-ToBe」です。これもググると出てきますが、すごく大切なので簡単に説明させてください。
ちなみに私は「AsIs-CanBe-ToBe」としてまとめて扱うことが多いです。
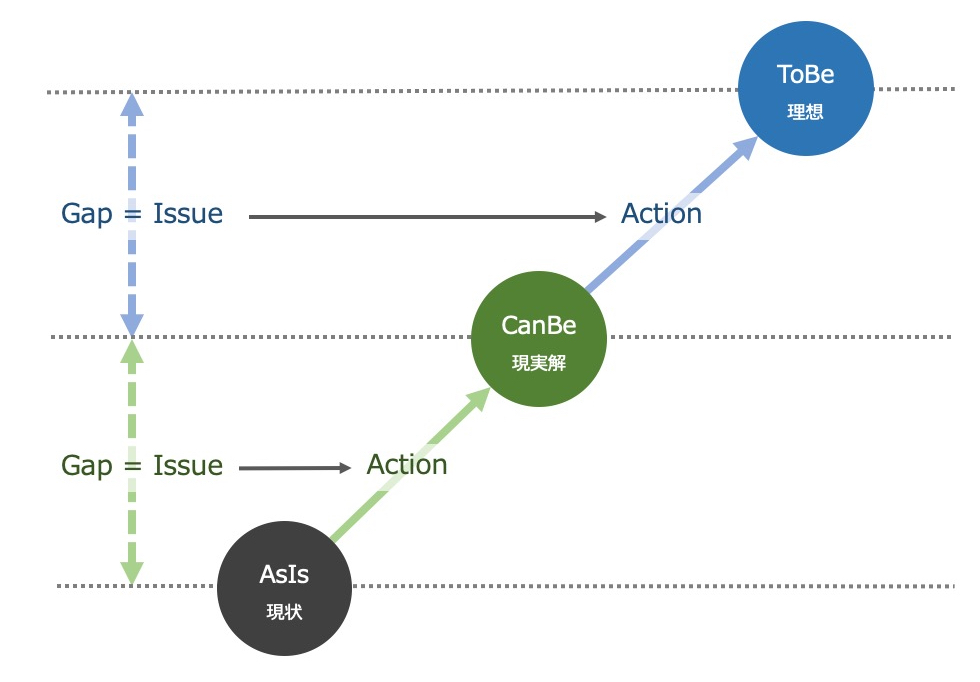
2-1. AsIs = 現状
AsIs は現状を正しく把握した状態です。
「正しく把握できていない状態」を AsIs とするとスタート地点を間違えてしまうため、まずは現状分析を行う事が必要です。
2-2. ToBe = 理想
ToBe は理想とする目標です。そのままですが、仕事をする上では AsIs と同様に明確化する必要があります。
例えば「エマ・ワトソンと結婚したい」など、具体的である必要があります。
2-3. CanBe = 現実解
CanBe は現実的な落とし所や中間目標です。
場合によっては複数の CanBe を経由して ToBe を目指すため、CanBe を当面の ToBe にすり替えることもあります。
例えば「エマ・ワトソンと出会うためにアメリカに移住」という具体的な中間目標を立てる、もしくは、
「エマ・ワトソンは難しいので、新垣結衣と結婚したい」など、やはり具体的な落とし所などになります。
2-4. Gap = 差分 と Issue = 課題
Gap は AsIs / CanBe / ToBe のそれぞれ間にある差分になります。
Gap があるということは、すなわち Issue が存在します。
この Issue の設定を間違えると、次の Action が本来目指すべき方向と異なる打ち手になってしまうので重要なフェーズです。
例えば「現状、新垣結衣と面識がない」などですね。
2-5. Action = 行動
Issue が明確になれば、あとは課題解決をすべく Action していくだけです!!
ここでも Issue に対して正しい Action を定義しているか?が大切になります。
例えば「新垣結衣と面識を持つために、TV 局前に張り込む」では、出会うのは難しそうです。
「新垣結衣と面識を持つために、TV 局に入社する」など、課題に対して効果のある Action を選ぶ必要があります。
2-6. CanBe が AsIs になる
Action 実行することで Issue を解決すると、もはや以前の AsIs は不要になります。
最終的な ToBe に向け、更に Gap => Issue => Action のループを回していくだけです!!
これでいつか新垣結衣と結婚でき、、、あ、私既婚者でした。ガッキーも結婚してた!
…(ひと呼吸)…
皆さんは原理原則に基づいた正しい ToBe を立ててくださいね!
3. 考える と 悩む の違い
最後に若手社員が陥りがちな罠「考える」と「悩む」の違いについてお伝えしたいと思います。
そういっても人は悩む生き物です。すべてがロジカルに判断できるとは限りません。
ガッキーへの思いを捨てきれない男子諸君は多いはずですっ!!(まだ引っ張るか)
でもこと仕事に関して言えば「悩む」より「考える」ことで前に進めていく必要があります。
2 つの違いを端的に言ってしまえば「結論に向かって建設的に思考しているか?」です。 つまり「考える」ためには以下を満たす必要があります。
- 結論があること
- 建設的に思考できること
ではどんな時に悩んでしまうのか、いくつかのパターンと対応策をお伝えしたいと思います。
ただし、いずれのパターンも「正しく考える」ことができれば「悩む」前に気付けるはずです。
3-1. 悩むパターン 1. 情報や知識が足りていない
もっともありがちなのはこのパターンかと思います。
例えば「A という作業を行うためには B という情報が必要」だったとします。
いまあなたが B という情報がない状態で「A という作業をやっておいて」という指示を受けた場合、まずは B の情報を得ることです。
ところがその B の情報を得ずに A を進めようとすると、それは悩んでしまします。
まずは「B が必要なんだ」という考えに至ること、もし知り得ない情報であれば「違和感に気付いて聞いてみる」必要があるでしょう。
3-2. 悩むパターン 2. 視野が狭くなっている
「原理と原則」の話をしましたが、この「原則」を意識していないために陥るパターンです。
暗黙の前提条件があるにも関わらず、思考の中でそれを使っていないことがあったりします。
「パターン 1.」とは違い、情報があるのにそれを活かせていないパターンです。
3-3. 悩むパターン 3. 思考順序を横着している
三段論法は多段で使うことでより効果を発揮します。というか、それが一般的です。
ですが必要な思考段階を横着する、多くの場合は「そうであるはず」と決め付けてしまい本筋からズレるパターンです。
このパターンは「経験者」ほどやってしまいがちですが、知識が少ない場合も強引にその知識を応用することで発生します。
常に、というのは難しいですが「原理原則に基づき」順序建てて考えることで回避できるはずです。
3-4. 悩むパターン 4. 答えがないことを考えようとしている
端的に言うと論理的に破綻してる、もしくは、答えが無数にあり確定しないパターンなどがこれです。
- 前者の例: 「絶対に損しない投資方法」
- 後者の例: 「人は何のために生きるのか?」
特に新卒のうちは「上司や先輩の言うことは絶対!」みたいな感覚になりがちですが、そうでもない事があります。
答えが出ないことに気付いたときは、「考え方の方向性を変える」もしくは「そもそも答えがないので、○○にしませんか?」などと相談するといいと思います。
ちなみに上司の中には(私がそうなのですが)、わざと「答えがない状態になる縛り」を含めて考えてみてもらうことがあります。性格が悪いですね!
意図としては「そのことに気付いて代替案などを出せるか?」を試すことで、仕様やアーキテクチャなどへの理解の深さを確認したりします。
おわりに
今回は「ロジカルシンキング編」と題して、主に基礎となる「数学的な考え方」と押さえて欲しい「AsIs-ToBe」についてまとめました。
特にプログラミングやシステム開発の世界では、ものづくりとことなり成果物のほとんどが可視化しづらいものになります。
突き詰めると「すべてがロジカルシンキング」であるため、是非身に付けてください。
そのためには「常に考える事を止めない」ことがもっとも大切ではないかと思います。

