はじめに
ニューラルネットワークが任意の関数を任意の精度で表現できる理由を、簡単に説明する。
Universal Approximation Theorem:普遍性定理
(1) 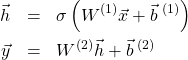
ここで、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() とした。また、
とした。また、![]() はステップ関数
はステップ関数
(2) ![]()
である。式(1)を成分で書くと
(3) 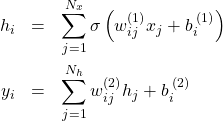
となる。式(3)の第1式を第2式に代入して
(4) 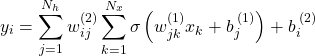
(5) ![Rendered by QuickLaTeX.com \begin{eqnarray*} y &=& \sum_{j=1}^{N_h} w^{(2)}_{j} \left[ \sigma\left(w^{(1)}_{j}x+b^{\;(1)}_j\right) \right] +b^{\;(2)}\\ &=& w^{(2)}_{1} \sigma\left(w^{(1)}_{1}x+b^{\;(1)}_1\right) + w^{(2)}_{2} \sigma\left(w^{(1)}_{2}x+b^{\;(1)}_2\right) +\cdots +w^{(2)}_{N_h} \sigma\left(w^{(1)}_{N_h}x+b^{\;(1)}_{N_h}\right) +b^{\;(2)} \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-d8e71d6b7f137a9cc7482f026beea206_l3.png)
となる。出力![]() はステップ関数を
はステップ関数を![]() 個だけ重ね合わせて表現されることが分かる。パラメータ
個だけ重ね合わせて表現されることが分かる。パラメータ![]() を調節することで各ステップ関数は
を調節することで各ステップ関数は![]() 軸に沿って左右に移動し、
軸に沿って左右に移動し、![]() を調節することで各ステップ関数の階段の高さが変化し、
を調節することで各ステップ関数の階段の高さが変化し、![]() を調節することで
を調節することで![]() を上下に動かすことができる。すなわち、中間層のユニット数
を上下に動かすことができる。すなわち、中間層のユニット数![]() を大きくし、パラメータを適当に調節することで任意の1次元関数
を大きくし、パラメータを適当に調節することで任意の1次元関数![]() を任意の精度で近似できることになる。下図は、ステップ関数を増やすことにより、いくらでも精度を高めることができることを表すイメージ図である。
を任意の精度で近似できることになる。下図は、ステップ関数を増やすことにより、いくらでも精度を高めることができることを表すイメージ図である。
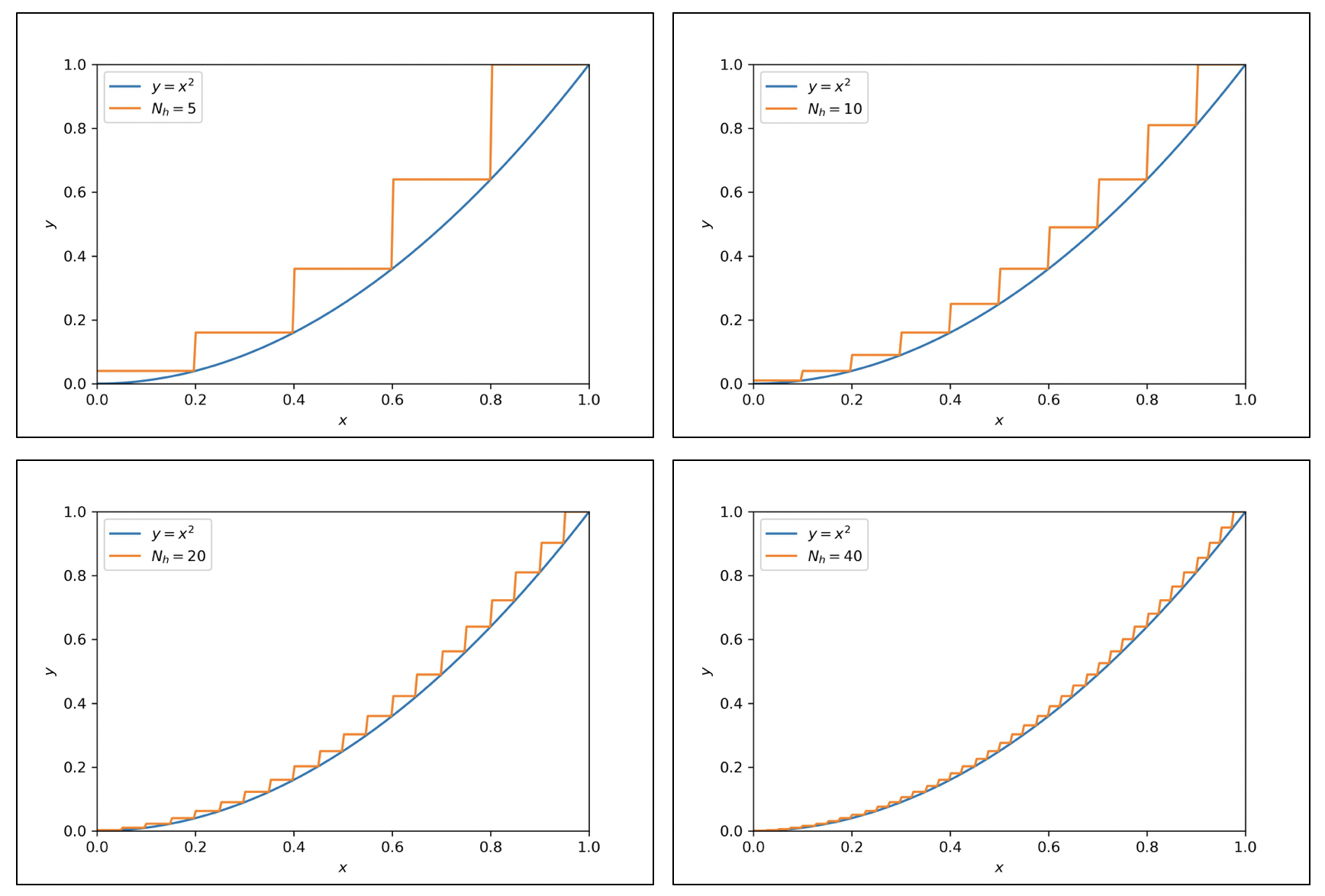
上で述べた事実は、一般の入出力![]() の場合に拡張することができる。すなわち、関数
の場合に拡張することができる。すなわち、関数![]() はニューラルネットワークを用いて近似できるのである。この事実をニューラルネットワークの普遍性定理と呼ぶ。
はニューラルネットワークを用いて近似できるのである。この事実をニューラルネットワークの普遍性定理と呼ぶ。
まとめ
今回は、ニューラルネットワークの精度の良さを説明する普遍性定理を紹介した。この定理では、活性化関数としてステップ関数を仮定しており、実際に使われる活性化関数(微分可能な関数)とは異なる。しかし、ニューラルネットワークがなぜ強力なのかを直感的に説明している。
ニューラルネットワークの表現力の高さは過剰適合(過学習)の原因でもあり、諸刃の剣であることに注意しなければならない。
参考文献
- ディープラーニングと物理学:深層学習の理論的背景に詳しい良書である。

