はじめに
今回は「テンソルネットワークの入り口」の2回目として、実際に深層学習に応用した例を紹介したい。今回のソースコードはここにある。
深層学習への応用
Googleの出しているテンソルネットワークのフレームワークTensorNetworkと、深層学習フレームワークTensorFlowを用いて、画像分類を行う。データセットはFashion-MNISTである。訓練データ数は60000、テストデータ数は10000、画像サイズは28![]() 28である。
28である。
テンソルネットワークを考える前のニューラルネットワークの構造は以下の通り(src/main_2.py)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def make_normal_network() -> tf.keras.Sequential: model = Sequential() # Declare a Sequential model model.add(Dense(512, input_shape=(784,))) model.add(Activation("relu")) model.add(Dropout(0.2)) model.add(Dense(512)) model.add(Activation("relu")) model.add(Dropout(0.2)) model.add(Dense(NUM_CLASSES)) model.add( Activation("softmax") ) return model |
全結合層だけを用いた構成である。入力画像のサイズは![]() であり、これをベクトルに引き延ばした
であり、これをベクトルに引き延ばした![]() 次元ベクトルが入力となる。一番最初(3行目)の全結合層を式で書くと
次元ベクトルが入力となる。一番最初(3行目)の全結合層を式で書くと
![]()
となる。ここで、![]() は
は![]() 次元ベクトル、
次元ベクトル、![]() は
は![]() 次元ベクトル、
次元ベクトル、![]() は
は![]() 行列、
行列、![]() は
は![]() 次元ベクトルとなる。上式を成分で書くと
次元ベクトルとなる。上式を成分で書くと
(1) ![]()
となる(アインシュタイン縮約記法を用いた)。図で示すと以下のようになる。
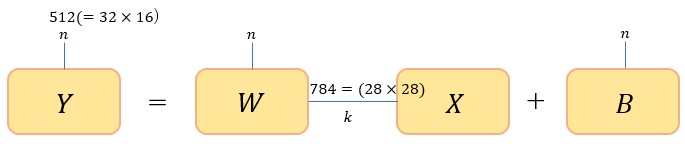
図7
さて、これをテンソルネットワークで表すため天下り的ではあるが以下のように書き換える。
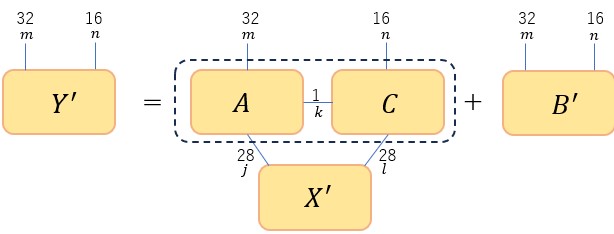
図8
つまり、1階テンソル![]() を2階テンソル
を2階テンソル![]() に変更し、
に変更し、![]() を点線の矩形内に示した2つのテンソルの積(MPS)に置換する。式で書くと
を点線の矩形内に示した2つのテンソルの積(MPS)に置換する。式で書くと
(2) ![]()
となる。![]() の次元を
の次元を![]() としたので、
としたので、![]() を
を![]() の行列とすることができる。先の説明では、MPSに置き換える際に特異値分解を用いた。上の表式に現れる
の行列とすることができる。先の説明では、MPSに置き換える際に特異値分解を用いた。上の表式に現れる![]() は学習により決まる行列であるから特異値分解を適用することはできない。そこで、
は学習により決まる行列であるから特異値分解を適用することはできない。そこで、![]() も学習から決まるテンソルとみなす。以上を実現するコードが以下である(src/tensor_network_layer_for_mnist.py)。このコードはTensorNetworkの公式が公開しているサンプルプログラムからの流用である。
も学習から決まるテンソルとみなす。以上を実現するコードが以下である(src/tensor_network_layer_for_mnist.py)。このコードはTensorNetworkの公式が公開しているサンプルプログラムからの流用である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
from typing import Any, Final import tensorflow as tf import tensornetwork as tn tn.set_default_backend("tensorflow") M: Final = 32 J: Final = 28 L: Final = 28 N: Final = 16 K: Final = 1 class TNLayer(tf.keras.layers.Layer): # type:ignore def __init__(self, m: int = M, j: int = J, l: int = L, n: int = N, k: int = K) -> None: # noqa super(TNLayer, self).__init__() # Create the variables for the layer. self.a_var = tf.Variable( tf.random.normal(shape=(m, j, k), stddev=1.0 / 32.0), name="a", trainable=True ) self.c_var = tf.Variable( tf.random.normal(shape=(n, l, k), stddev=1.0 / 32.0), name="c", trainable=True ) self.bias = tf.Variable(tf.zeros(shape=(m, n)), name="bias", trainable=True) self.j = j self.m = m self.n = n self.l = l # noqa def call(self, inputs: Any) -> Any: # Define the contraction. # We break it out so we can parallelize a batch using # tf.vectorized_map (see below). def f( input_vec: Any, a_var: tf.Variable, c_var: tf.Variable, bias_var: tf.Variable ) -> tn.Tensor: # Reshape to a matrix instead of a vector. input_vec = tf.reshape(input_vec, (self.j, self.l)) # Now we create the network. a = tn.Node(a_var) c = tn.Node(c_var) x_node = tn.Node(input_vec) a[1] ^ x_node[0] c[1] ^ x_node[1] a[2] ^ c[2] # The TN should now look like this # | | # a --- b # \ / # x # Now we begin the contraction. d = a @ x_node result = (d @ c).tensor # To make the code shorter, we also could've used Ncon. # The above few lines of code is the same as this: # result = tn.ncon([x, a_var, b_var], [[1, 2], [-1, 1, 3], [-2, 2, 3]]) # Finally, add bias. 32x32の行列ができる。32x32=1024 return result + bias_var # To deal with a batch of items, we can use the tf.vectorized_map # function. # https://www.tensorflow.org/api_docs/python/tf/vectorized_map result = tf.vectorized_map(lambda vec: f(vec, self.a_var, self.c_var, self.bias), inputs) return tf.reshape(result, (-1, self.m * self.n)) |
4行目のtensornetworkがテンソルネットワークのモジュールである。8行目から12行目までの変数名は式(2)周辺で用いた変数名と一致させている。20行目のself.a_varが![]() に、23行目の
に、23行目のself.c_varが![]() に、26行目の
に、26行目のself.baisが![]() に相当する。40行目から65行目までのコードが式(2)の計算に対応する。
に相当する。40行目から65行目までのコードが式(2)の計算に対応する。tensornetworkの使い方に関しては公式のチュートリアルを見てほしい。
最初に示した全結合層だけのネットワーク構造の中の最初の層だけを上のクラスのインスタンスで置き換える。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def make_network_with_tensor_network() -> tf.keras.Sequential: model = Sequential() model.add(tnl.TNLayer()) model.add(Activation("relu")) model.add(Dropout(0.2)) model.add(Dense(512)) model.add(Activation("relu")) model.add(Dropout(0.2)) model.add(Dense(NUM_CLASSES)) model.add( Activation("softmax") ) return model |
3行目がテンソルネットワークで置き換えた層である。それ以外の層は変えていない。さて、パラメータの保存に必要なメモリ量を第1層について計算してみる。式(1)の右辺の成分の総数![]() は、
は、![]() であるから行列
であるから行列![]() の要素数が
の要素数が![]() 、
、![]() の要素数が512となり、これらを足し合わせて
の要素数が512となり、これらを足し合わせて![]() となる。一方、式(2)の右辺のパラメータの総数
となる。一方、式(2)の右辺のパラメータの総数![]() は、
は、![]() の次元を
の次元を![]() とすると、
とすると、![]() の成分数が
の成分数が![]() 、
、![]() の成分数が
の成分数が![]() 、
、![]() の成分数が
の成分数が![]() なのでこれらを足し合わせて
なのでこれらを足し合わせて![]() となる。
となる。![]() のときメモリ量を節約できることになる。この式を評価すると
のときメモリ量を節約できることになる。この式を評価すると![]() であれば良いことになる。今回の計算では
であれば良いことになる。今回の計算では![]() とした。従って
とした。従って![]() となり大幅な削減を実現できる。以下に計算結果を示す。
となり大幅な削減を実現できる。以下に計算結果を示す。
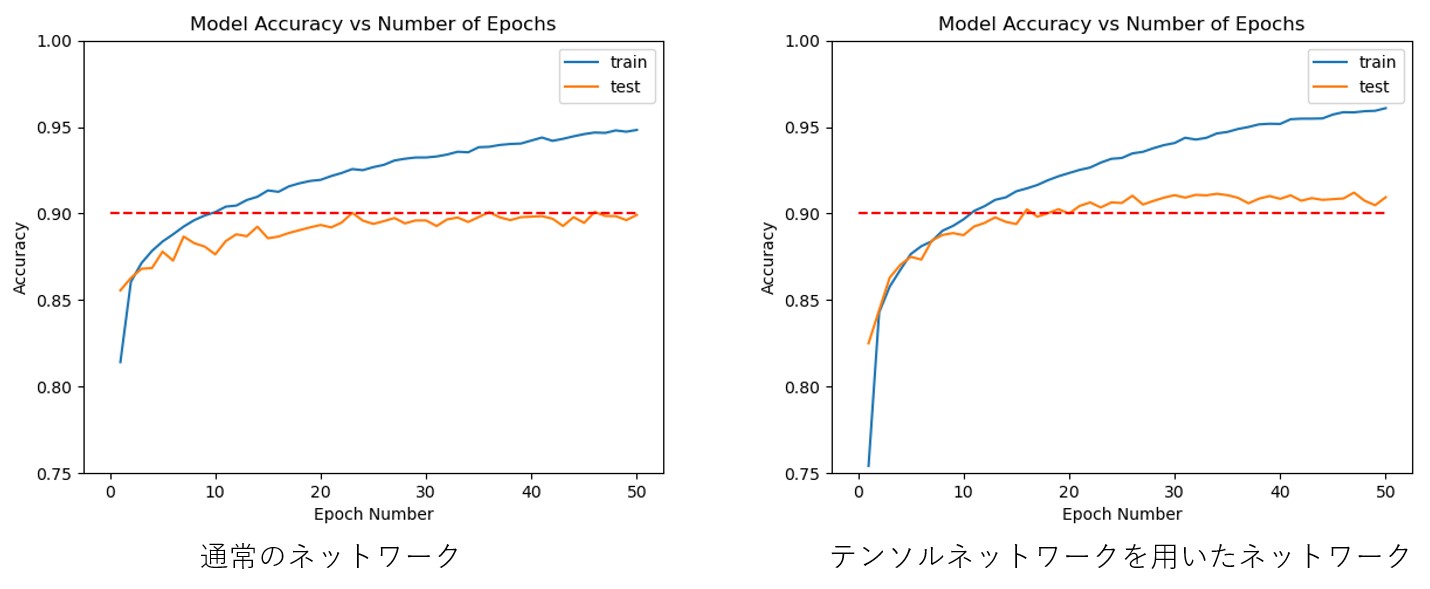
図9
精度を維持しつつ(少し良くなっている)、ネットワーク容量を圧縮できた。
まとめ
今回は、テンソルネットワークを使うことで、精度を維持しつつニューラルネットワークのパラメータ数を大幅に減らすことができることを見た。全結合層以外へのテンソルネットワークの応用についても今後調べたい。

