はじめに
今回は、機械学習の分野でもしばしば聞くようになってきたテンソルネットワークを紹介する。テンソルネットワークとは、物性物理や統計力学の分野で発展してきた計算手法である(と私は理解している)。この分野で開発された計算手法が、近年、量子コンピュータや機械学習の分野にも応用されるになってきた。
テンソルとは
テンソルネットワークを説明する前に、テンソルについて説明する。まず最初に、![]() 次元ベクトル
次元ベクトル![]() を考える。
を考える。
![]()
ベクトルの要素は添え字1つの変数![]() で表すことができる。次に、
で表すことができる。次に、![]() の行列
の行列![]() を考える。
を考える。

この要素は添え字2つの変数![]() で表すことができる。添え字1つの変数がベクトルを、添え字2つの変数が行列を表した。これを一般化して任意の個数の添え字を持つ変数を考える。
で表すことができる。添え字1つの変数がベクトルを、添え字2つの変数が行列を表した。これを一般化して任意の個数の添え字を持つ変数を考える。
![]()
この変数で表される量をテンソルと呼ぶ(厳密なテンソルの定義は例えば[1]を参照のこと)。ベクトルは1階テンソル、行列は2階テンソルである。また、スカラは0階テンソルに相当する。図で示すと以下のようになる。
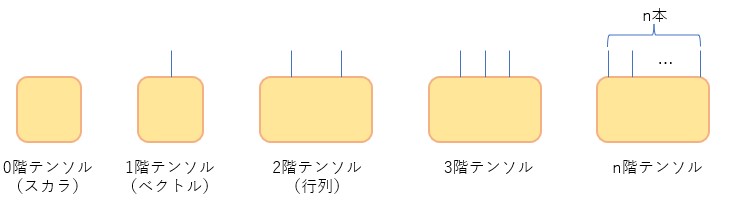
図1
テンソルネットワークとは
線形代数によると、任意の![]() 行列
行列![]() を特異値分解することができる(証明は線形代数の教科書を参照のこと)。
を特異値分解することができる(証明は線形代数の教科書を参照のこと)。
![]()
ここで、![]() は
は![]() の一般化されたユニタリ行列、
の一般化されたユニタリ行列、![]() は
は![]() のユニタリ行列、
のユニタリ行列、![]() は
は![]() の対角行列(対角成分は全て非負実数)である。また、
の対角行列(対角成分は全て非負実数)である。また、![]() は
は![]() のエルミート共役を表す。上式を成分で書くと
のエルミート共役を表す。上式を成分で書くと
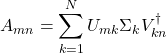
となる。![]() のときの様子は以下の通り。
のときの様子は以下の通り。
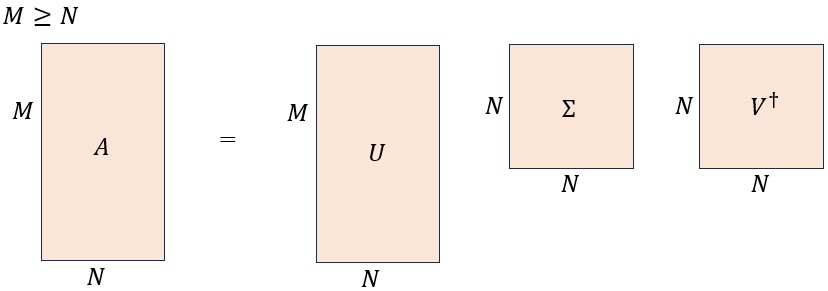
図2
いま、
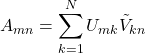
となり、再び行列で表記すると
![]()
となる。さて、この変形の過程を図で示すと以下になる。
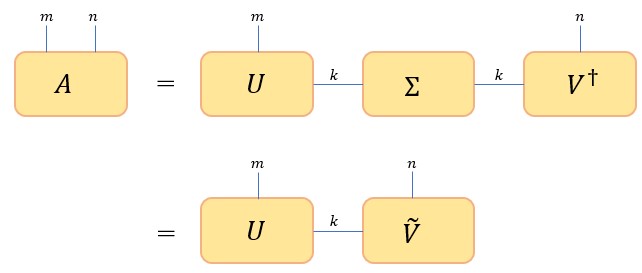
図3
この変形は下図のように一般化できる(証明は略)。

図4
(1) ![]()
となる。上式において、2度出現する添え字については和をとるという約束をし、和記号を省略した(アインシュタイン縮約記法)。テンソルネットワークとは、階数の大きなテンソル(例えば上の![]() )を、階数の小さなテンソル(例えば上の
)を、階数の小さなテンソル(例えば上の![]() や
や![]() )の積に分解したものである。式(1)は、テンソルネットワークの一例であり、Matrix Product State(MPS)と呼ばれる。その他のテンソルネットワークの例を図4に示す(引用元)。下図では各テンソルが丸で表記されていることに注意する。また、それぞれの名称についてもここでは言及しない。いろいろな分解の仕方があるという点だけを抑えておけばよい(詳細は私も知らない)。
)の積に分解したものである。式(1)は、テンソルネットワークの一例であり、Matrix Product State(MPS)と呼ばれる。その他のテンソルネットワークの例を図4に示す(引用元)。下図では各テンソルが丸で表記されていることに注意する。また、それぞれの名称についてもここでは言及しない。いろいろな分解の仕方があるという点だけを抑えておけばよい(詳細は私も知らない)。
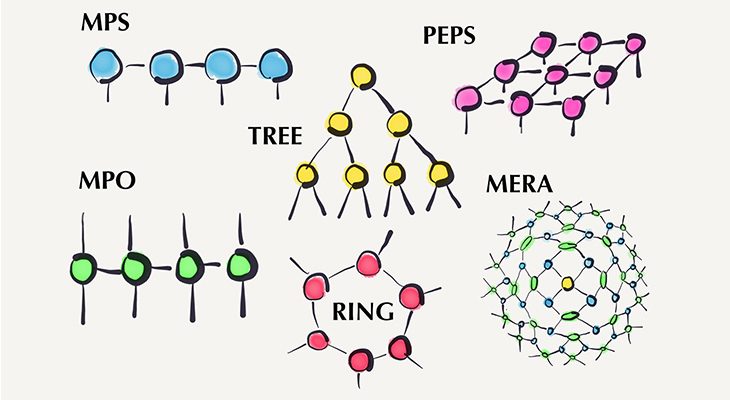
図5
テンソルネットワークのご利益
大きなテンソルを小さなテンソルに分解すると何がうれしいのかを見るために、上で議論した特異値分解を再度とりあげる。
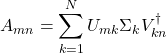
ここで、![]() は
は![]() の行列、
の行列、![]() は
は![]() の一般化されたユニタリ行列、
の一般化されたユニタリ行列、![]() は
は![]() のユニタリ行列である。また、行列
のユニタリ行列である。また、行列![]() は
は![]() の正方対角行列であり、要素は全て非負の実数である。対角成分は左上から右下に向けて降順に並んでおり、0が並ぶこともあり得る。図で書くと以下のようになる。
の正方対角行列であり、要素は全て非負の実数である。対角成分は左上から右下に向けて降順に並んでおり、0が並ぶこともあり得る。図で書くと以下のようになる。
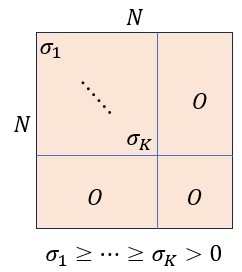
図6
さて、![]() 番目以降の対角成分が0となる場合
番目以降の対角成分が0となる場合
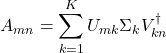
と書くことができる。![]() のとき下図の緑色の領域が計算に寄与する部分である。
のとき下図の緑色の領域が計算に寄与する部分である。
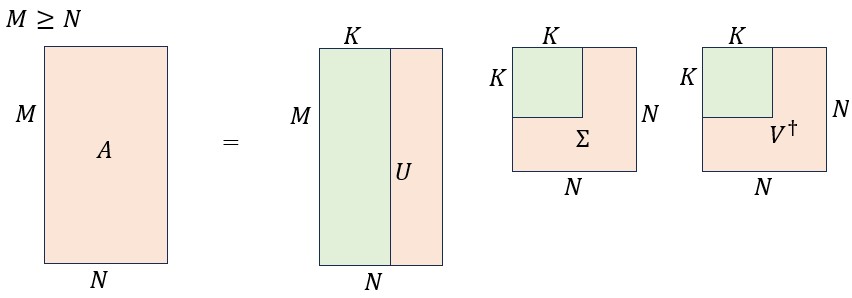
図7
このとき、計算に寄与する![]() の成分数は
の成分数は![]() 、
、![]() の成分数は
の成分数は![]() 、
、![]() の成分数は
の成分数は![]() であるから、右辺の総成分数は
であるから、右辺の総成分数は![]() となる。一方、左辺の
となる。一方、左辺の![]() の成分数は
の成分数は![]() である。いま、
である。いま、![]() 、
、![]() として見積もってみると左辺の成分数は
として見積もってみると左辺の成分数は![]() 、右辺の成分数は
、右辺の成分数は![]() となる。同じテンソルを保存するために必要とされる容量を節約できることが分かる。0に近い特異値も適度に無視するようにすればもっと節約することができる。このことは一般のMPSに対しても成り立つ。つまり下図の右辺のテンソル間をつなぐ添え字
となる。同じテンソルを保存するために必要とされる容量を節約できることが分かる。0に近い特異値も適度に無視するようにすればもっと節約することができる。このことは一般のMPSに対しても成り立つ。つまり下図の右辺のテンソル間をつなぐ添え字![]() の取り得る次元を減らすことができれば記憶容量を節約できるのである(もちろん、添え字
の取り得る次元を減らすことができれば記憶容量を節約できるのである(もちろん、添え字![]() の取り得る次元を減らすということは近似に相当するので、精度と記憶容量というトレードオフは発生する)。
の取り得る次元を減らすということは近似に相当するので、精度と記憶容量というトレードオフは発生する)。

図8
まとめ
今回は、テンソルネットワークの触りの部分だけを紹介した。私自身もこの手法に関しては素人なので、テンソルネットワークに関するこれ以上の深い議論はしないことにする。次回は、今回紹介したMPSを深層学習のネットワークに適用し、精度を維持しつつ重みパラメータの数を劇的に減らすことができる例を紹介したい。

