はじめに
GAN(Generative Adversarial Network)による画像生成の進歩には目覚ましいものがある。今回は、GANを訓練する際に使われるminmax戦略を簡潔に説明する。
GANとは
GANは、生成器(Generator)と識別器(Discriminator)を競い合わせて学習を行うネットワークである(下図参照)。
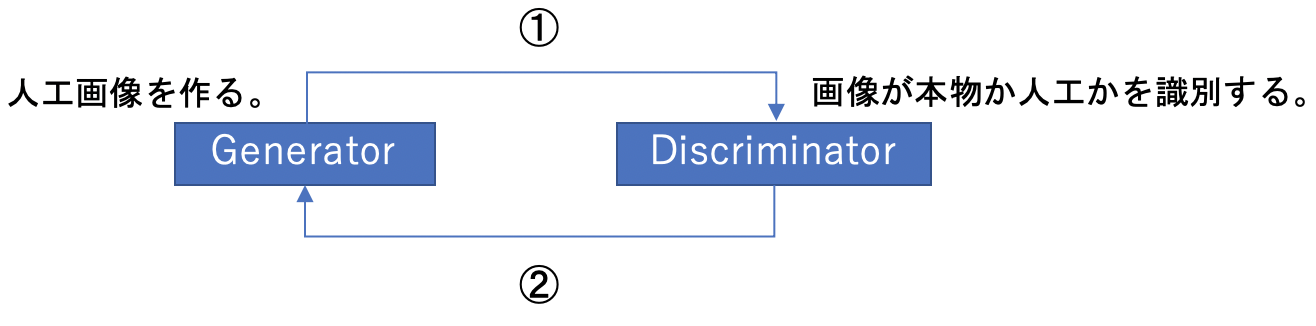
Generatorで人工画像を作成し、Discriminatorで本物か否かを識別する(①)。結果のフィードバックを受けてGeneratorが改良され、再び人工画像が作られる(②)。この繰り返しにより、より本物に近い画像が作られていくことになる。これが、GANの仕組みである。次節で、この手順を数式を用いて説明する。
GANのminmax戦略
(1) ![]()
ここで、![]() は画像、
は画像、![]() は本物の画像が従う確率分布、
は本物の画像が従う確率分布、![]() は人工画像が従う確率分布、
は人工画像が従う確率分布、![]() は識別関数を表す。
は識別関数を表す。![]() は本物の画像を入力したとき大きな値を出力し、人工画像を入力したとき小さな値を出力する関数である。
は本物の画像を入力したとき大きな値を出力し、人工画像を入力したとき小さな値を出力する関数である。![]() は、生成器
は、生成器![]() に依存することに注意する。
に依存することに注意する。
式(1)の右辺第1項が小さくなるのは![]() が大きい時、すなわち、本物の画像を正しく本物であると識別できた場合である。一方、式(1)の右辺第2項が小さくなるのは、人工画像を本物でないと識別できた時である。つまり、式(1)を最小化することで最適な識別器
が大きい時、すなわち、本物の画像を正しく本物であると識別できた場合である。一方、式(1)の右辺第2項が小さくなるのは、人工画像を本物でないと識別できた時である。つまり、式(1)を最小化することで最適な識別器![]() が求まることになる。次に
が求まることになる。次に
(2) 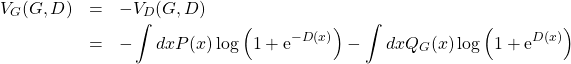
を考える。式(2)の右辺第1項が小さくなるのは、本物の画像を人工画像であると識別した場合である。第2項が小さくなるのは、人工画像を本物であると識別した場合である。つまり、式(2)を最小化することで最適な生成器![]() を決めることができる。以上の議論をまとめると、最適な
を決めることができる。以上の議論をまとめると、最適な![]() と
と![]() は次式から決定されることになる。
は次式から決定されることになる。
(3) ![]()
これがGANの損失関数の最適化に使われるminmax戦略である(下図参照)。
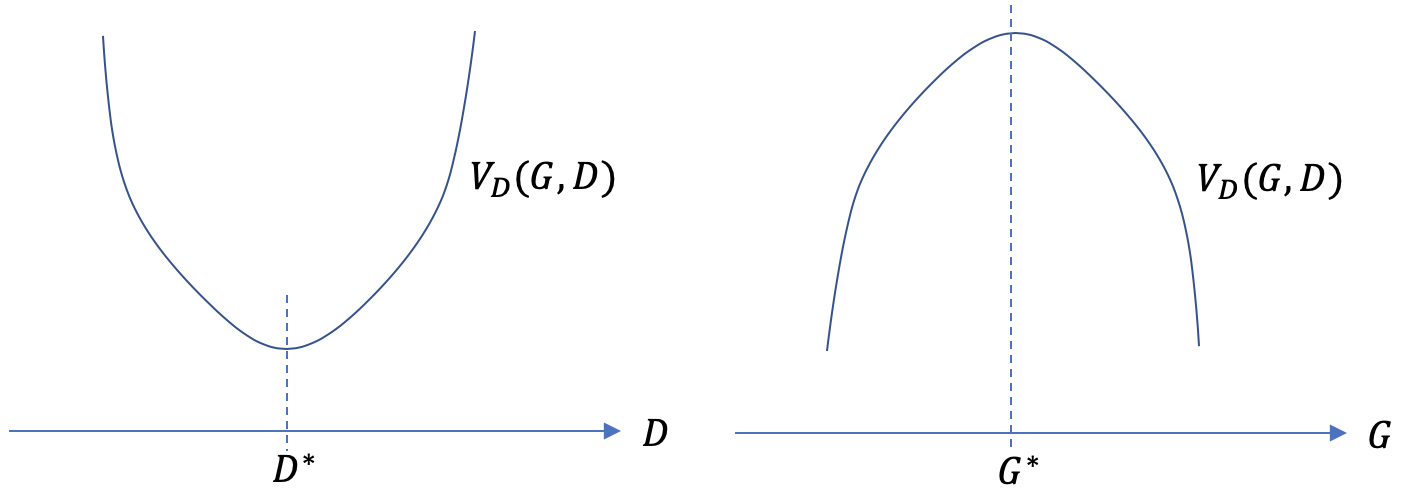
minmaxの数理
式(3)から最適な生成器![]() を求めることができる。
を求めることができる。![]() の導出とは、確率分布
の導出とは、確率分布![]() を決めることに他ならない。
を決めることに他ならない。![]() は人工画像が従う確率分布であるから、この分布が本物の画像が従う分布
は人工画像が従う確率分布であるから、この分布が本物の画像が従う分布![]() に一致するのが理想である。本節では、式(3)からを
に一致するのが理想である。本節では、式(3)からを![]() が導出されることを見る。
が導出されることを見る。
(4) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \delta V_D &=& V_D(G,D+\delta D)-V_D(G,D) \nonumber \\ &=& \int dx P(x) \left[ \log{\left(1+{\rm e}^{-\left(D(x)+\delta D(x)\right)}}\right)} -\log{\left(1+{\rm e}^{-D(x)}}\right)} \right]\nonumber\\ &+& \int dx Q_G(x) \left[ \log{\left(1+{\rm e}^{D(x)+\delta D(x)}}\right)} -\log{\left(1+{\rm e}^{D(x)}}\right)} \right]\nonumber\\ &=& \int dx P(x)\delta D(x) \frac{ \partial \left( \log{ \left( 1+{\rm e}^{-D(x)} \right) } \right) } {\partial D(x)} \nonumber\\ &+& \int dx Q_G(x)\delta D(x) \frac{ \partial \left( \log{ \left( 1+{\rm e}^{D(x)} \right) } \right) } {\partial D(x)} \nonumber\\ &=& \int dx\delta D(x) \left[ \frac{-P(x){\rm e}^{-D(x)}}{1+{\rm e}^{-D(x)}} +\frac{Q_G(x){\rm e}^{D(x)}}{1+{\rm e}^{D(x)}} \right] \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-fae803cdeac6575fa0918c641d9d99a7_l3.png)
![]() のとき、任意の
のとき、任意の![]() について
について![]() となるから
となるから
(5) ![]()
これを変形すると
(6) ![]()
を得る。これが、最適な![]() の満たす式である。これを式(1)に代入すると
の満たす式である。これを式(1)に代入すると
(7) 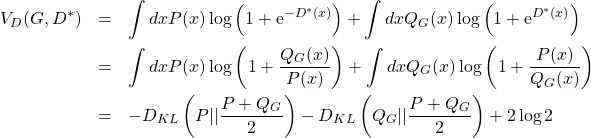
を得る。ここで![]() は次式で定義されるKullback-Leibler divergenceである。
は次式で定義されるKullback-Leibler divergenceである。
(8) ![]()
![]() は任意の
は任意の![]() について
について![]() となるとき最小値0を取る。この事実を用いると、式(7)が最大となるのは
となるとき最小値0を取る。この事実を用いると、式(7)が最大となるのは
(9) ![]()
のとき、すなわち
(10) ![]()
のときである。以上から、![]() が導出された。
が導出された。
まとめ
今回は、GANの損失関数をminmax戦略を用いて最適化すると、![]() が導出されることを確認した。実際の学習では、理論通りには行かず、様々な不安定性が引き起こされることが分かっている。この不安定性を取り除く研究が精力的に行われ、現在の高画質な画像を実現したわけである。下図はBigGANと呼ばれる手法により生成された画像の一例である(参照論文)。
が導出されることを確認した。実際の学習では、理論通りには行かず、様々な不安定性が引き起こされることが分かっている。この不安定性を取り除く研究が精力的に行われ、現在の高画質な画像を実現したわけである。下図はBigGANと呼ばれる手法により生成された画像の一例である(参照論文)。
参考文献
- ディープラーニングと物理学:深層学習の理論的背景に詳しい良書である。


