はじめに
今回はバイナリー・クロスエントロピーについて解説する。最近読んだテキストに丁寧な導出過程が書かれていたので、いまさらと言われそうだが紹介したい。
2分類問題の設定
バイナリー・クロスエントロピーは2分類問題に使われる損失関数であるから最初に2分類問題の設定を行う。
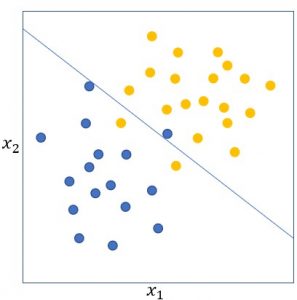
図1
2次元座標上に分布する2種類のデータを考える(上図参照)。各点の属するクラスは色で識別されている(青と橙)。ここでの目的は、この2種類の点の分布を上手く分割する境界面を見つけることである。
バイナリー・クロスエントロピーの導出
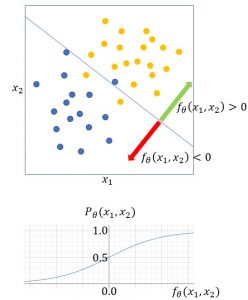
図2
(1) ![]()
と書くことができる。![]() は与えられたデータから求める値である。一般に境界面の上下で
は与えられたデータから求める値である。一般に境界面の上下で![]() の正負は入れ替わり(図では上側で正、下側で負とした)、絶対値
の正負は入れ替わり(図では上側で正、下側で負とした)、絶対値![]() の値は境界から離れるにつれて大きくなる。
の値は境界から離れるにつれて大きくなる。![]() から
から![]() までの任意の値を取る
までの任意の値を取る![]() はシグモイド関数
はシグモイド関数
![]()
を用いて確率に変換することができる(図2の下図)。
![]()
境界面上(![]() )で
)で![]() である。図では境界上側で
である。図では境界上側で![]() としたから、
としたから、![]() は図の緑の矢印方向に向かうほど1に近くなる。つまり、
は図の緑の矢印方向に向かうほど1に近くなる。つまり、![]() は、点が橙色である確率とみなすことができる。見方を変えれば、
は、点が橙色である確率とみなすことができる。見方を変えれば、![]() は点が青色である確率である。各点にラベル
は点が青色である確率である。各点にラベル![]() という属性を付加し、橙色のとき
という属性を付加し、橙色のとき![]() 、青色のとき
、青色のとき![]() とすると、次のように書くことができる。
とすると、次のように書くことができる。
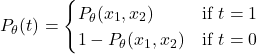
上式は以下のように1式で表現できる。
![]()
![]() に存在する点が橙色であるなら
に存在する点が橙色であるなら![]() が大きくなるように、その点が青色であるなら
が大きくなるように、その点が青色であるなら![]() が大きくなるように(つまり、
が大きくなるように(つまり、![]() が小さくなるように)境界面のパラメータを決めれば良い。点は複数個あるから次式を最大にすることが目的となる。
が小さくなるように)境界面のパラメータを決めれば良い。点は複数個あるから次式を最大にすることが目的となる。
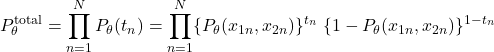
添え字![]() で個々の点を表し、点の総数を
で個々の点を表し、点の総数を![]() とした。各点は独立同分布に従うと仮定するので各点の確率をかければよい。両辺の対数を取ると
とした。各点は独立同分布に従うと仮定するので各点の確率をかければよい。両辺の対数を取ると
![Rendered by QuickLaTeX.com \begin{align*} L(\theta)\equiv\ln{P_{\theta}^{\rm total}}= \sum_{n=1}^N \ln{P_{\theta}(t_n)}=\sum_{n=1}^N\Bigl[ t_n\ln{P_{\theta}(x_{1n},x_{2n})} +(1-t_n) \ln{\{1-P_{\theta}(x_{1n},x_{2n})\}} \Bigr] \end{align*}](/wp-content/ql-cache/quicklatex.com-c562b5b09155ef4a82f54cbf1e999508_l3.png)
を得る。この式がバイナリ・クロスエントロピー(![]() )である。
)である。![]() を最大にする
を最大にする![]() を求める問題に帰着した。一般に、ある事象が実現する尤度(つまり確率)を最大にするようなパラメータ決定法を最尤推定法と呼ぶ。
を求める問題に帰着した。一般に、ある事象が実現する尤度(つまり確率)を最大にするようなパラメータ決定法を最尤推定法と呼ぶ。
上の計算では、確率への変換式にシグモイド関数を用いたが、境界面上で0.5を取り、境界の一方へ向かうと1に、もう一方に向かうと0になる滑らかな単調増加関数であれば任意の関数を選ぶことができる。
まとめ
今回は、バイナリ・クロスエントロピーの式が、確率的な考え方から導出できることを示した。多くの教科書では天下り的に与えられている式なので参考になればと思う。
参考文献

