はじめに
Adding Problemは、学習時に長期記憶を必要とする典型的な問題である。今回はこの問題を、ChainerのNStepLSTMを用いて実装する。
Adding Problem
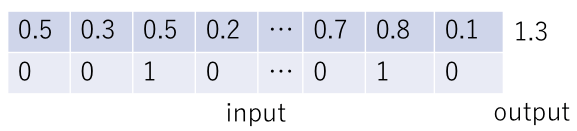
Adding Problemの入出力の作成手順は以下の通りである(下図参照)。
- 長さ
 の配列を用意し、0から1の間で定義される一様乱数を用いて値を決定する(図の最初の行)。
の配列を用意し、0から1の間で定義される一様乱数を用いて値を決定する(図の最初の行)。 - 配列の要素にランダムに0か1を割り振る。(図の2行目)。これをマスク値と呼ぶことにする。1を与える要素は2つだけである。
- マスク値1を持つ2つの要素の和を出力とする(図の最初の行の右端に記した数値)。
前回までの議論(LSTM, NStepLSTM)では、入力値・出力値の次元はともに1であったが、今回は入力値の次元は2、出力値の次元は1となる。入力値の最初の次元には乱数の値、次の次元にはマスク値(0 or 1)を格納する。変数で表現すれば以下のようになる。
- 入力値:

- 出力値:

ここで、![]() は用意するデータの個数である。入力値は3階のテンソルであり、添字
は用意するデータの個数である。入力値は3階のテンソルであり、添字![]() と
と![]() を固定したとき
を固定したとき![]() は2つの値(乱数値とマスク値)をとる2次元ベクトルになる。ネットワークは、ランダムに選ばれた任意の2つの数の和を予測できるように訓練される。その際、
は2つの値(乱数値とマスク値)をとる2次元ベクトルになる。ネットワークは、ランダムに選ばれた任意の2つの数の和を予測できるように訓練される。その際、![]() が長くなるほど長期記憶が必要になる。
が長くなるほど長期記憶が必要になる。
アーキテクチャ
今回のネットワークの構造を以下に示す。
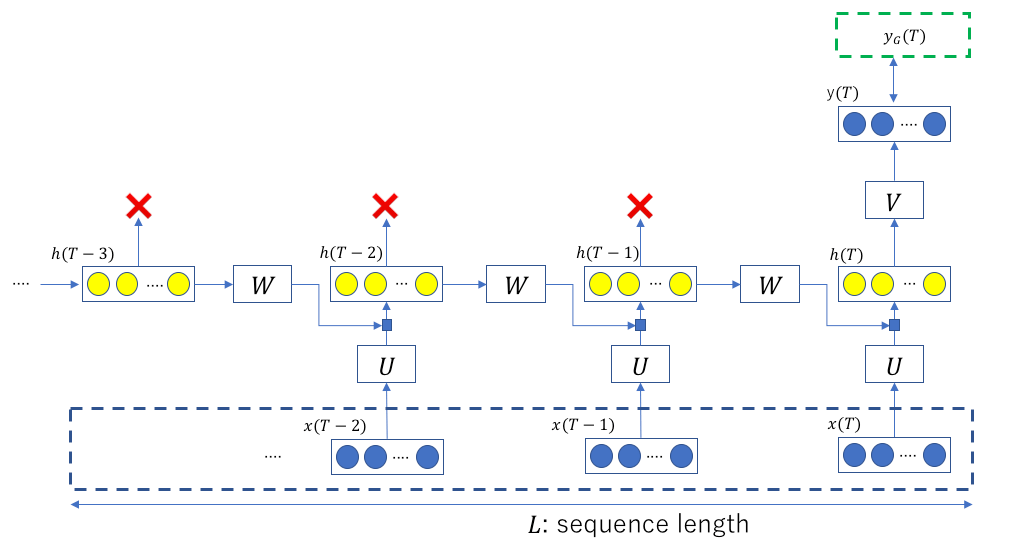
これまでのLSTMを用いた実装では、赤バツで示した出力値も損失関数の計算に使用していたが(LSTMの式(2)の上図を参照)、今回は一番最後の出力値だけを使い損失関数を評価する。青い点線矩形が入力シーケンス、緑の点線矩形![]() がGround Truthである。この値と
がGround Truthである。この値と![]() との間の誤差が最小となるように訓練される。
との間の誤差が最小となるように訓練される。
ソースの場所
今回のソースはここにある。訓練時に使用するファイルは「nstep_lstm_using_chainer_with_adding_problem.py」、描画に使用したJupyterファイルは「draw_results_with_adding_problem.ipynb」である。
各種パラメータの設定
計算時に使用するパラメータの値を以下に示す(params_for_adding_problem.py)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#!/usr/bin/env python # -*- coding: utf-8 -*- # LSTM層の数 N_LAYERS = 1 DROPOUT = 0.5 # 時系列データの全長 TOTAL_SIZE = 10000 # 訓練とテストの分割比 SPRIT_RATE = 0.9 # 入力時の時系列データ長 SEQUENCE_SIZE = 200 EPOCHS = 100 BATCH_SIZE = 100 # 入力層の次元 N_IN = 2 # 隠れ層の次元 N_HIDDEN = 200 # 出力層の次元 N_OUT = 1 GPU = 0 SEED = 0 |
TOTAL_SIZEはデータの個数![]() に、SEQUENCE_SIZEは
に、SEQUENCE_SIZEは![]() に相当する値である。N_INとN_OUTはそれぞれ入力値の次元、出力値の次元である。
に相当する値である。N_INとN_OUTはそれぞれ入力値の次元、出力値の次元である。
結果
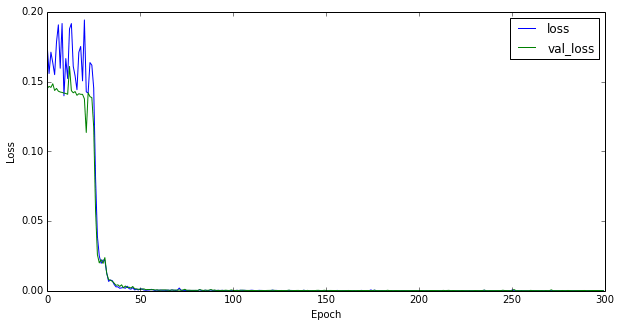
最初に学習曲線を示す。エポック数は100とした。
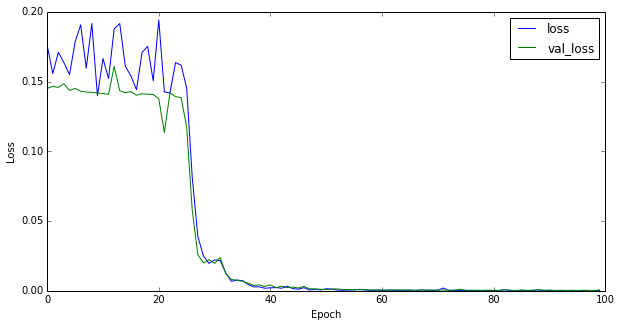
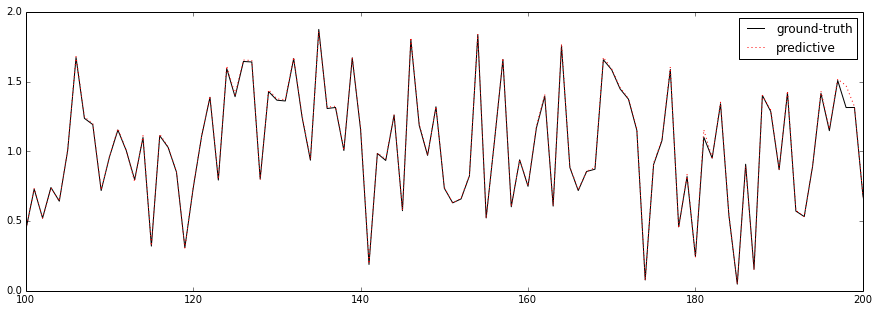
これまでの学習曲線は指数関数的に減衰するのが常であったが、今回の振る舞いはそれとはかなり異なる。最初はほとんど減衰していかないが、あるエポック数を境に急激に減衰する。下図はテストデータに適用したときの予測結果(点線)である。実線はGround Truthである。
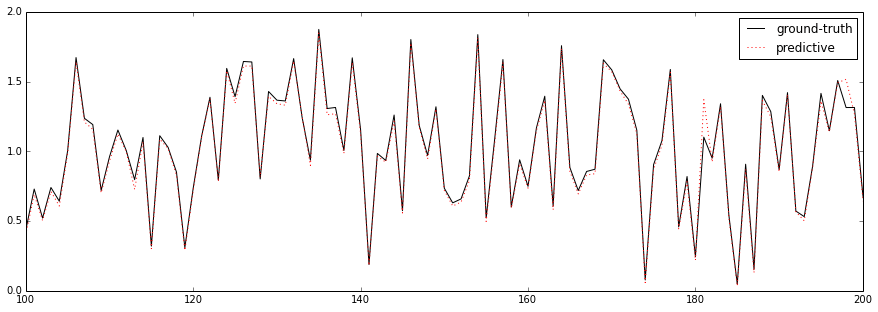
縦軸は出力値![]() (2つの乱数の和)、横軸は
(2つの乱数の和)、横軸は![]() (
(![]() の行列)である。エポック数を300とした結果は以下の通りである。
の行列)である。エポック数を300とした結果は以下の通りである。
定量的な精度を見るため、予測値![]() とGround Truth
とGround Truth ![]() の間の平均2乗誤差
の間の平均2乗誤差
(1) 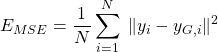
を以下に示す。
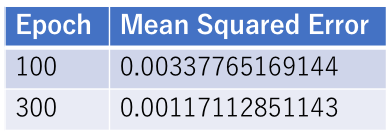
以上から、LSTMは長期記憶を適切に扱えることが分かる。
まとめ
今回は、長期記憶が必要とされるAdding Problemを取り上げ、Chainer.NStepLSTMを用いて実装を行なった。実行結果を示し、長期記憶を学習する際に観察される特異な学習曲線を示した。今回のような問題の場合、パターンを把握するまでは損失はほとんど減らないが、一度理解してしまうと急激に損失関数が減衰する。
擬人的に表現するとどうなるであろうか?「全くわからん、わからん、わからん、。。。あれっ? わかった! 楽勝じゃん」

