はじめに
今回は、Delaunay三角形分割とその双対構造であるVoronoi図について説明する。
Delaunay三角形分割とは
いま3次元空間内で定義される関数![]() を考える。関数の形状は未知であり、観測点
を考える。関数の形状は未知であり、観測点![]() における値のみが既知であるとする(下図参照:ここから引用した)。
における値のみが既知であるとする(下図参照:ここから引用した)。
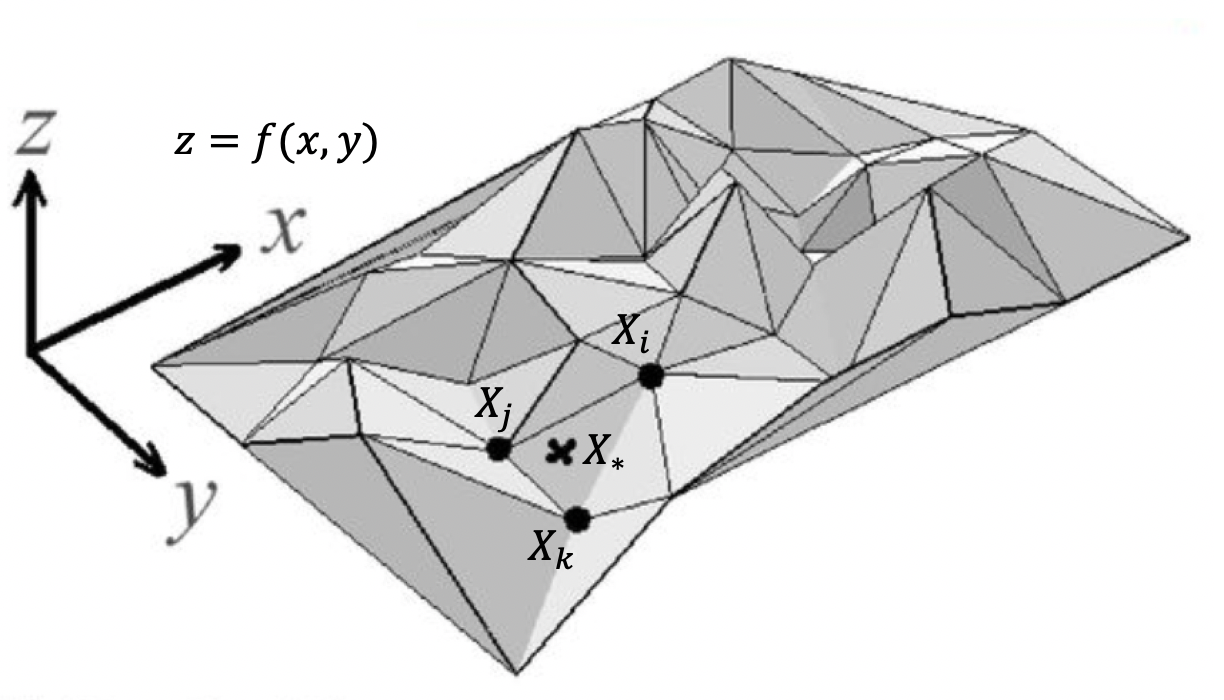
3つの観測点![]() の近傍にある未観測点
の近傍にある未観測点![]() における
における![]() の値を予測したいとき、以下の手順を考えることができる。
の値を予測したいとき、以下の手順を考えることができる。
- 点
 を囲む、3つの観測点から構成される三角形を見つける。
を囲む、3つの観測点から構成される三角形を見つける。 - この三角形の頂点における関数の値は既知である。適当な加重平均を計算し、
 を求める。
を求める。
上の手順を実現するには、2次元平面を観測点![]() を頂点とする三角形に分割しなければならない(下図参照:ここから引用した)。
を頂点とする三角形に分割しなければならない(下図参照:ここから引用した)。
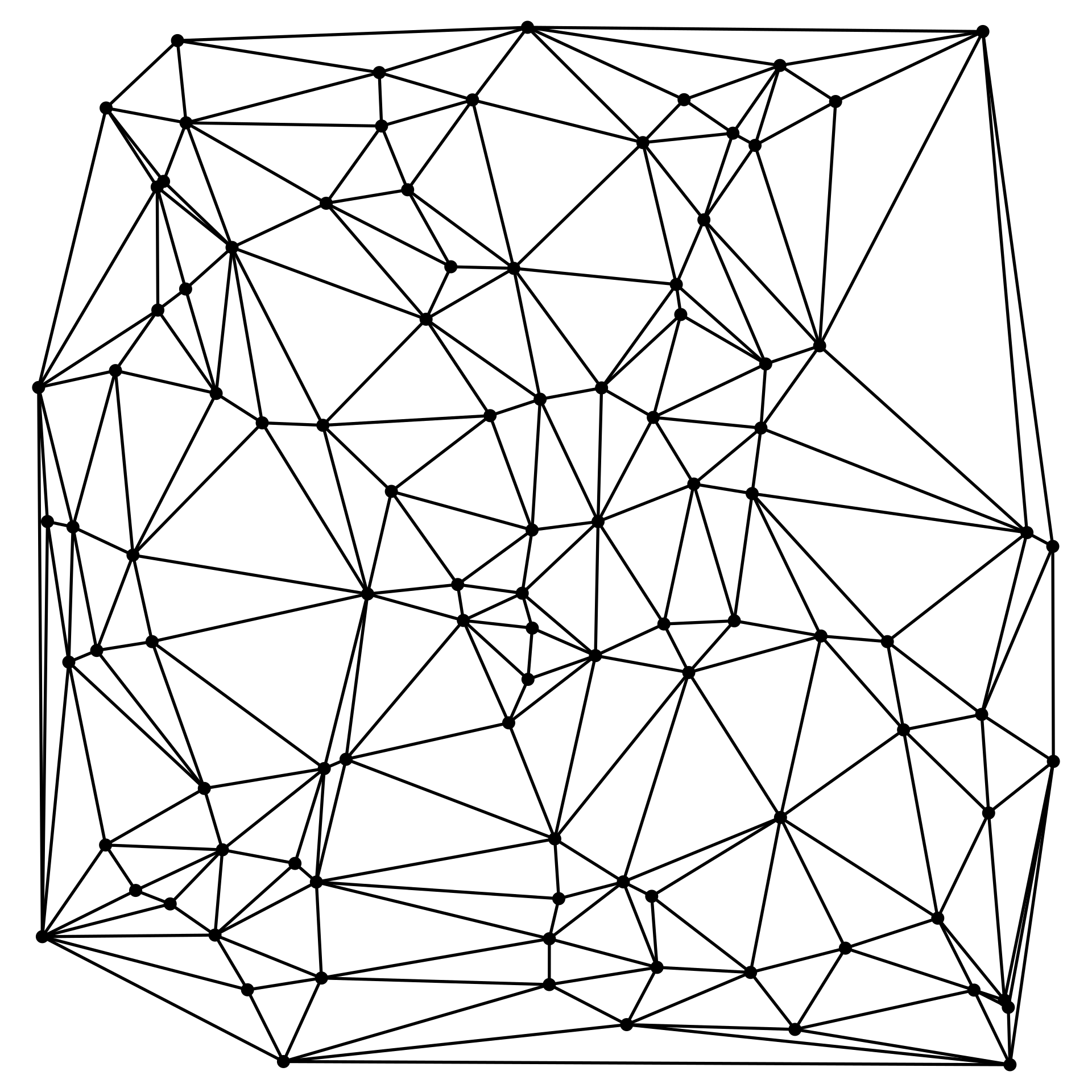
このときよく使われる手法がDelaunayの三角形分割である。この分割手法は有限要素法を行う際のメッシュ生成にも使われている。
Delaunay三角形分割の定義
平面上の点の集合(母点集合)を![]() とする。
とする。![]() から3つの母点
から3つの母点![]() を取り出し、これら3点のみを円周上に持ち、この3点以外の母点を円内に持たないような円が存在するとき、この3点を頂点とする三角形を作る。これを繰り返したのものがDelaunay三角形分割である(下図参照)。
を取り出し、これら3点のみを円周上に持ち、この3点以外の母点を円内に持たないような円が存在するとき、この3点を頂点とする三角形を作る。これを繰り返したのものがDelaunay三角形分割である(下図参照)。
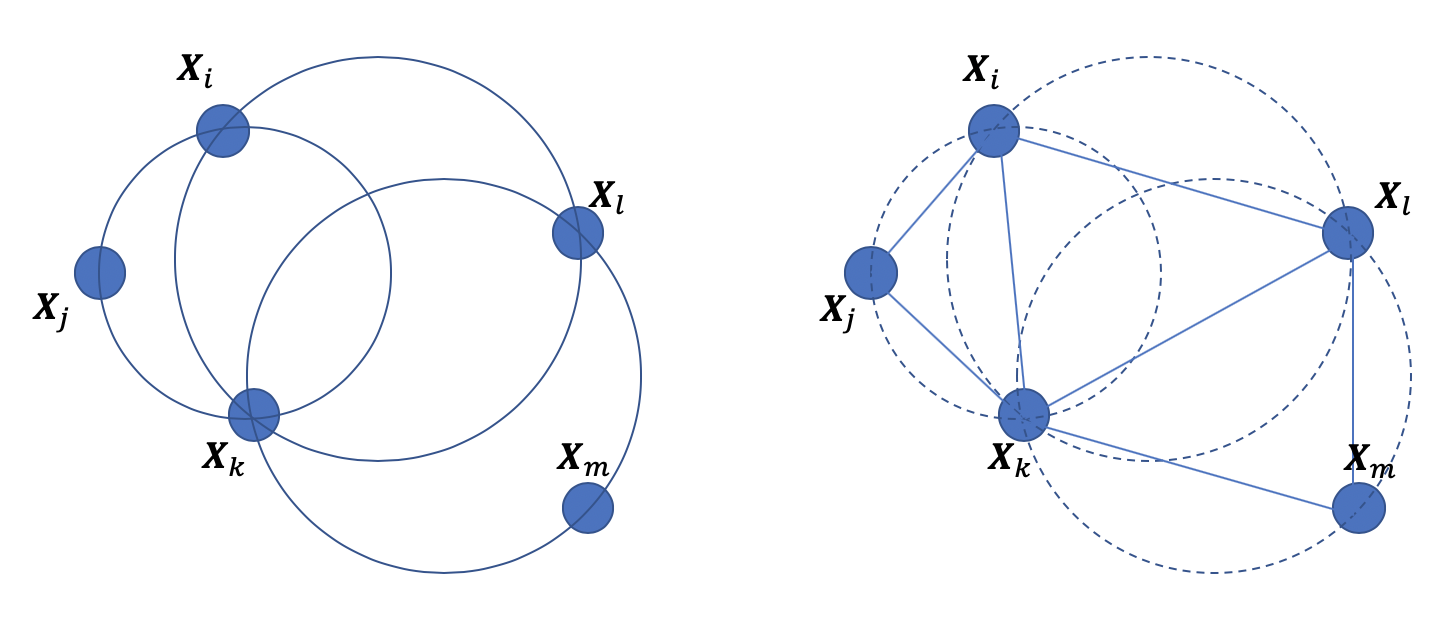
この分割により、2次元平面は「ふっくら」とした三角形に分割される。
双対構造:Voronoi図
Delaunay三角形分割が実現できれば、これと双対な構造であるVoronoi図を容易に作ることができる(下図参照:ここから引用した)。
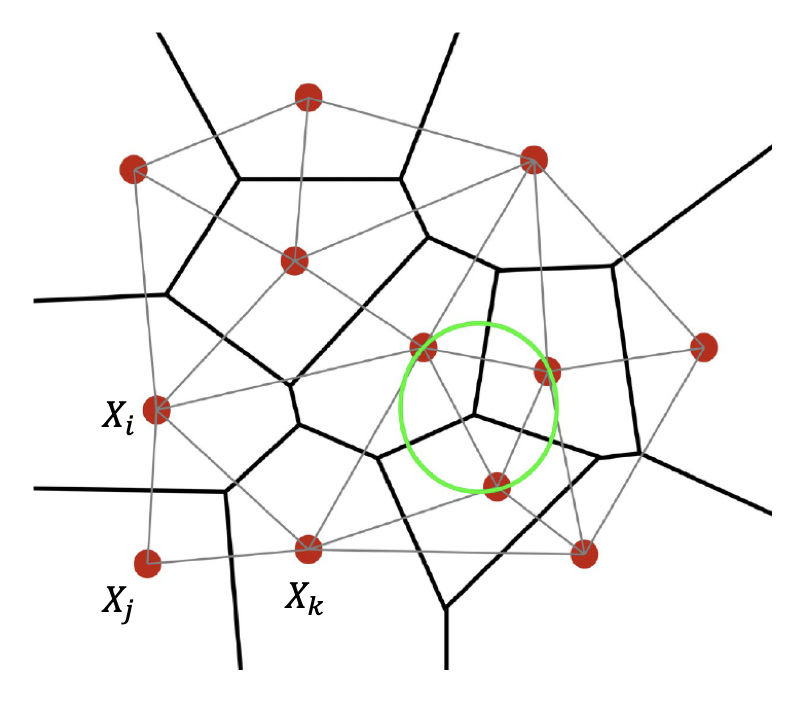
上図の赤点(母点)を結ぶ構造がDelaunay三角形分割であり、母点を細胞核のように内部にもつ領域の集まりがVoronoi図である。Voronoi図の生成手順は以下の通りである。
- 三角形
 の外接円
の外接円 の中心を求める。
の中心を求める。 - 三角形
 が隣接するとき
が隣接するとき の中心を結ぶ。
の中心を結ぶ。 - これを繰り返す。
例えば母点![]() を内部に持つVoronoi領域
を内部に持つVoronoi領域![]() を考える。この領域内の任意の点
を考える。この領域内の任意の点![]() と全母点との距離を考えたとき、
と全母点との距離を考えたとき、![]() に最も近い母点は
に最も近い母点は![]() である。つまり、母点
である。つまり、母点![]() が「支配」する領域が
が「支配」する領域が![]() である。ひとつの適用例としてWorld Airports Voronoiなるものがある。これは世界中の空港の位置を母点としたVoronoi図である。
である。ひとつの適用例としてWorld Airports Voronoiなるものがある。これは世界中の空港の位置を母点としたVoronoi図である。
実装
Delaunay三角形分割とVoronoi図はともにOpenCVに実装されているので、これを利用する。サンプルコードは以下の通りである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
#include <iostream> #include <random> #include <vector> #include <opencv2/opencv.hpp> #include <cpplinq.hpp> #include <boost/range/irange.hpp> // size of a window constexpr int IMAGE_SIZE{1000}; cv::Mat initialize_canvas(const std::vector<cv::Point2f>& points); void calculate_voronoi(cv::Subdiv2D& subdiv, const std::vector<cv::Point2f>& points, cv::Mat& canvas); void calculate_delaunay(cv::Subdiv2D& subdiv, const std::vector<cv::Point2f>& points, cv::Mat& canvas); int main(int argc, const char * argv[]) { // make random points std::mt19937 mt{}; std::uniform_int_distribution<int> distribution{0, IMAGE_SIZE - 1}; std::vector<cv::Point2f> points{}; constexpr int N_POINTS{100}; points.reserve(N_POINTS); for ([[maybe_unused]] auto i : boost::irange(0, N_POINTS)) { auto x = distribution(mt); auto y = distribution(mt); points.emplace_back(x, y); } // make an object cv::Subdiv2D subdiv{}; subdiv.initDelaunay(cv::Rect(0, 0, IMAGE_SIZE, IMAGE_SIZE)); subdiv.insert(points); // make a delaunay triangulation auto canvas = initialize_canvas(points); calculate_delaunay(subdiv, points, canvas); cv::imwrite("/Users/kumada/Projects/cct_blog/voronoi/opencv_voronoi/opencv_voronoi/delaunay.jpg", canvas); // make a voronoi diagram canvas = initialize_canvas(points); calculate_voronoi(subdiv, points, canvas); cv::imwrite("/Users/kumada/Projects/cct_blog/voronoi/opencv_voronoi/opencv_voronoi/voronoi.jpg", canvas); return 0; } cv::Mat initialize_canvas(const std::vector<cv::Point2f>& points) { // display random points cv::Mat canvas = cv::Mat::zeros(IMAGE_SIZE, IMAGE_SIZE, CV_8UC3); for (const auto& point: points) { cv::circle(canvas, point, 4, cv::Scalar(0, 0, 255), -1); } return canvas; } void calculate_voronoi(cv::Subdiv2D& subdiv, const std::vector<cv::Point2f>& points, cv::Mat& canvas) { // prepare output containers std::vector<int> idx{}; std::vector<std::vector<cv::Point2f>> facet_lists{}; std::vector<cv::Point2f> facet_cernters{}; // calculcate voronoi subdiv.getVoronoiFacetList(idx, facet_lists, facet_cernters); // display voronoi structure for (const auto& list: facet_lists) { auto before = list.back(); for (const auto& point: list) { cv::Point p1{static_cast<int>(before.x), static_cast<int>(before.y)}; cv::Point p2{static_cast<int>(point.x), static_cast<int>(point.y)}; cv::line(canvas, p1, p2, cv::Scalar(64, 255, 128)); before = std::move(point); } } } void calculate_delaunay(cv::Subdiv2D& subdiv, const std::vector<cv::Point2f>& points, cv::Mat& canvas) { std::vector<cv::Vec4f> edge_list{}; subdiv.getEdgeList(edge_list); for (const auto& edge: edge_list) { cv::Point p1{static_cast<int>(edge.val[0]), static_cast<int>(edge.val[1])}; cv::Point p2{static_cast<int>(edge.val[2]), static_cast<int>(edge.val[3])}; cv::line(canvas, p1, p2, cv::Scalar(48, 128, 48)); } } |
これを実行すると以下の画像を得る。母点の数は1000である。最初の画像がDelaunay三角形分割、後の画像が同じ母点に対するVoronoi図である。


まとめ
今回は、Delaunay三角形分割とVoronoi図を紹介した。両者とも応用例の大変多い構造である。

