はじめに
CCTが提供している調達DX(調達DX ~見積もり自動化技術~|CCT)では、AIや3D CADデータを使用して製造業の見積もり自動化技術を提供しています。今回は、製造業の場面で使用される3Dデータの相互変換について取り上げます。
近年の3Dデータの需要やソフトウェアの発展に応じて、様々なタイプの3Dのデータ形式が生まれてきました。それに伴って、「異なるデータ形式間でもうまく変換して相互にデータのやり取りをしたい!」というケースも当然生じてきます。こちらの記事(CADデータの受け渡し)でも紹介されている通り、そのような場合に対応するための手段の一つとして、「変換したいデータをいったん中間データという、3D形状を三角形の集合としてあらわすメッシュデータや、点の集合としてあらわす点群データに変換したうえで、別のデータ形式に変換する」というものがあります。中間データの代表例は次のようなものがあります:
| 形式(拡張子) | 説明 |
| STLファイル形式(.stl) | 三次元形状を三角形要素の集合として表現する形式。プレーンテキストで記述されたASCII形式とバイナリ形式の二つがある。STL形式(Wikipedia) |
| PLYファイル形式(.ply) | 三次元形状を点情報と面情報の集合として表現する形式。色や透過度の値も持つことができる。プレーンテキストで記述されたASCII形式とバイナリ形式の二つがある。PLY形式(Wikipedia) |
| STPファイル形式(.stp, .step) | 三次元形状をNURBS曲線・曲面と呼ばれる数学的な曲線や曲面で表現する形式。データの精度が高いという特徴がある。STP(STEP)形式(Wikipedia) |
今回はこれらの中間データ同士の変換の例として、点群データをメッシュデータに変換する方法を考えていきます。
点群データをメッシュデータに変換するには
点群データは専用の3Dスキャナーを利用することで「手軽に・素早く・広範囲にデータを取得できる」という特徴から近年建設の分野などでの活用が注目を集めています。一方で、メッシュデータには「データ構造が単純でデータが扱いやすく、軽量である」というメリットがあり、場面や目的に応じてそれぞれのデータ形式を往来することでより優れたDXを達成することができます。
点群をメッシュにするアルゴリズムはいくつか知られています。代表的なものは次の二つです:
Ball-Pivoting Algorithm
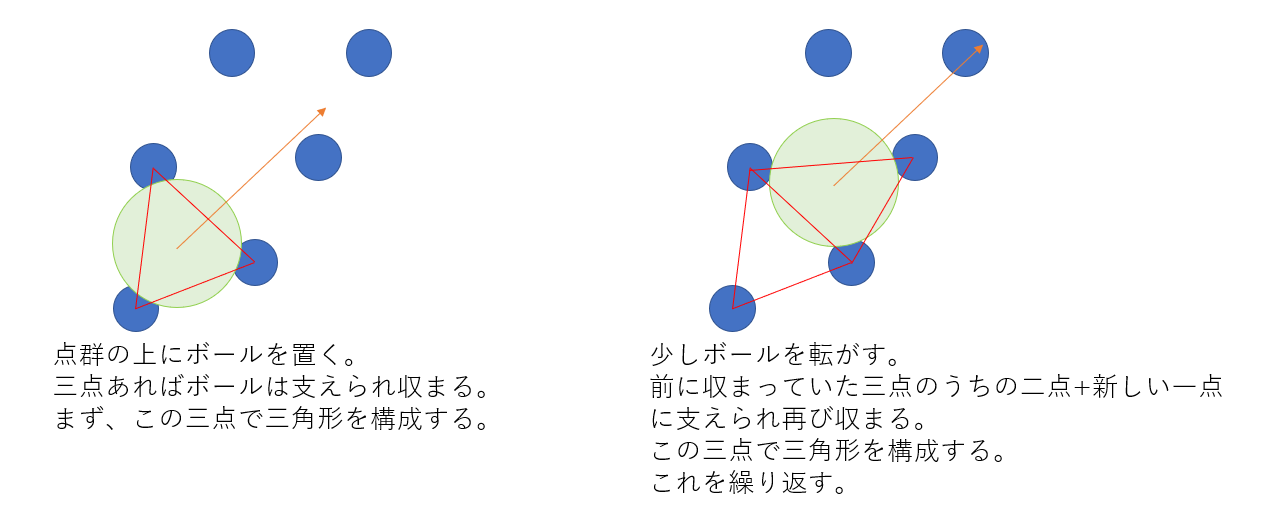
このアルゴリズムでは、点群は「中身のない」ものである必要があります。つまり、点は表面だけを構成していなければなりません。そのような点群の上に適当なボールを落としてみます。ボールは点に引っ掛かり、表面上に留まります。その時にボールは三点と接触します。この三角形を起点として、ボールを少し転がしてみましょう。すると、前の三角形の二点プラスあたらしい一点でまた引っ掛かります。このように、ボールをどんどん転がして三角形を作っていきメッシュにします。
Poisson Reconstruction
こちらのアルゴリズムはより高等数学的です。ざっくりいえば、モデルの「内側」と「外側」を区別するような関数を作って、その関数に従って膜で覆うようにしてメッシュを作ろう、という発想になります。アルゴリズムの考案者(M. Kazhdan)によると、「ノイズデータに強い」という特徴があるようです。論文はこちらです(Poisson Surface Reconstruction)
Open3Dについて
Open3D(Open3D公式)は、3Dデータ処理用オープンソースライブラリです。PythonとC++で使用することができます。
点群をメッシュに変換するにあたっては、変換のアルゴリズムはもちろん、点に対する法線推定などの下処理も労力が大きいです。Open3Dを使用することで、それらの手間を省き、かつより品質の高い結果を高速に得ることができます。また、点群データのメッシュ化についてOpen3Dは先に挙げた二つのアルゴリズムに加え、Alpha Shapesというアルゴリズムも使用することができます。ここで言及した3つのアルゴリズムを含め、Open3Dのメッシュ化については公式ドキュメントに詳しく記載があります。Open3D公式(Surface Reconstruction)
Open3DはPython向けに書かれた記事が多いため、今回はC++でやってみようと思います。
実際にやってみよう
Open3Dの導入はOpen3D公式のGetting Startedを見てみてください。
今回はOpen3Dに実装されているBall Pivoting Algorithmを用いて点群のPLYファイルをメッシュのSTLファイルに変換してみましょう。
コマンドは次のようなものにしてみます:
$[exe名] [入力ファイル] [出力ファイル]
メイン部分のコードはこんな感じになりました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
// コマンド引数から点群のデータを読み取りcloud_ptに格納 auto cloud_ptr = std::make_shared(); io::ReadPointCloud(argv[2], *cloud_ptr) // 各点に対する頂点を推定 const auto radius_for_serch = 0.01; // 点の近傍の検索範囲 const auto max_nn = 50; // 点の法線推定で考慮する最大の近傍点数 cloud_ptr->EstimateNormals(geometry::KDTreeSearchParamHybrid(radius_for_serch , max_nn)); // 点が持つ法線の青銅上昇のため、点の属する面に対する法線の一貫性を保つようにする cloud_ptr->OrientNormalsConsistentTangentPlane(10); // Ball Pivoting Algorithmの実行 const auto distances = cloud_ptr->ComputeNearestNeighborDistance(); const auto avg_dist = [distances]() -> double { double total = 0.0; for (const auto dist : distances) { total += dist; } return total / static_cast(distances.size()); }(); const auto radius = 2 * avg_dist; // Ball Pivotin Algorithmにおいて転がすボールの半径 std::vector rad_vec = {radius, radius * 2}; const auto rec_mesh_BPA = geometry::TriangleMesh::CreateFromPointCloudBallPivoting(*cloud_ptr, rad_vec); // 点群から構成されたメッシュデータをSTLファイルとして書き出す io::WriteTriangleMesh(argv[3], *rec_mesh_BPA); |
実験
実験としてリンゴの点群モデルをメッシュモデルに変換してみます。
今回はこちらのサイト(PLY Files an ASCII Polygon Format)の「apple.ply」を手元のメモ帳でコピー&ペーストして使用しました。
ファイルを見る際はOpen3Dのexamplesにあらかじめ同梱されている「Visualizer.exe」をビルドして使用しています。
元のplyファイルを表示するとこちらのようになります。
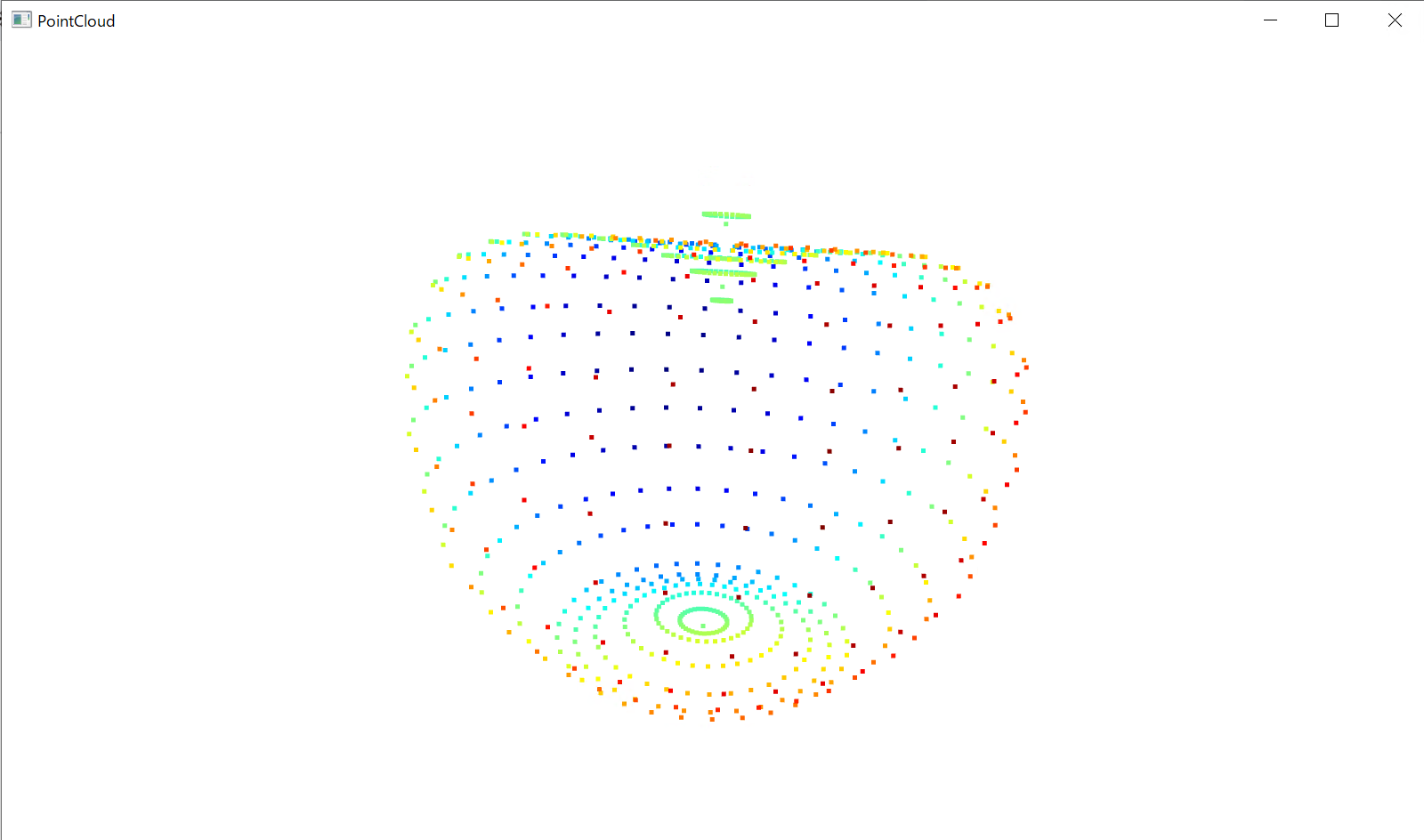
早速PLYファイルをSTLファイルに変換してみましょう。
変換後のstlファイルを表示してみるとこのようになりました。

概ねいい感じなのですが、穴が開いてしまっているのと、枝の部分は構成されませんでした。枝の部分は点が密集しており法線方向の推定の精度があまりよくないためこのような結果になっているのかもしれません。より良い結果を得るためには途中のパラメータを細かくチューニングする必要があるようです。
おわりに
お疲れさまでした。今回はOpen3DとC++でBall-Pivoting Algorithmを用いて点群からメッシュ変換(PLYからSTL)をしてみました。点群データもメッシュデータもそれぞれ利点があり、相互に変換することが容易になればモデルの解析精度向上などが見込めると思います。今回はply形式からstl形式への変換を試みましたが、その他の中間ファイル同士の組み合わせも挑戦してみたいです。読んでいただきありがとうございました。

