はじめに
こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第 6 回目です。
第 1 回～第 5 回までで、ソートに関するアルゴリズムを見ていきました。
本記事の末尾にまとめておきますので、そちらを見ていただけますと幸いです。
今回から探索に関するアルゴリズムを考えていきたいと思います。
探索とは
探索とは複数のデータの中から条件に一致した値をみつけることを指します。
単純に探索といっても種類があり、それぞれにアルゴリズムがあり探索効率が変わってきます。
アルゴリズムを考えてみる
本日は以下の探索に関してアルゴリズムを考えていきます。
今回の以下 2 つの探索は配列に対して探索を行います。
- 線形探索
- 二分探索
線形探索
概要
線形探索は最も単純な探索アルゴリズムです。
配列の先頭から順に値を比較していって一致すれば探索を終了し、一致しなければ次の要素と比較していきます。
オーダー
先頭から順に末尾まで比較を繰り返すので、 
です。
処理
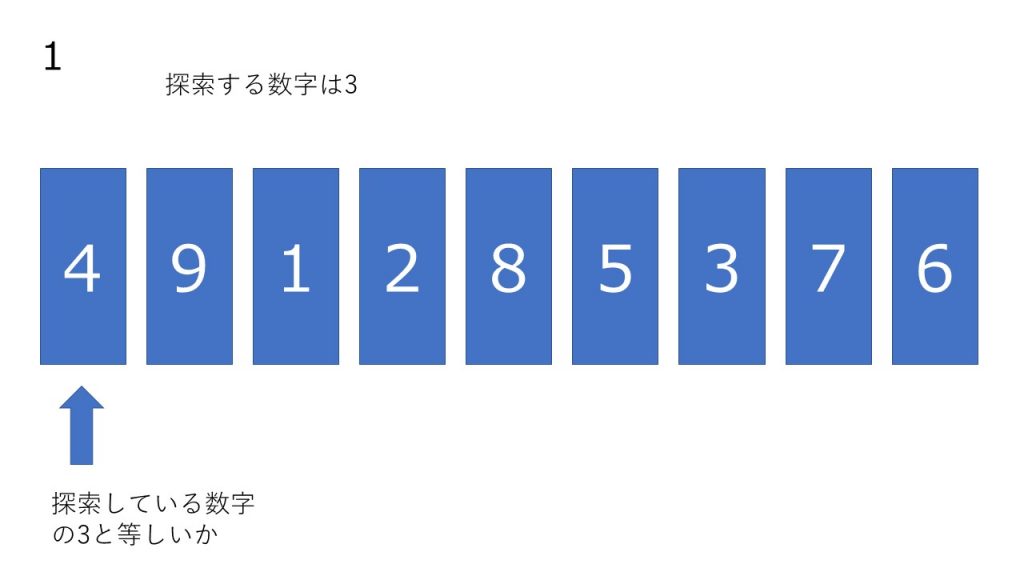
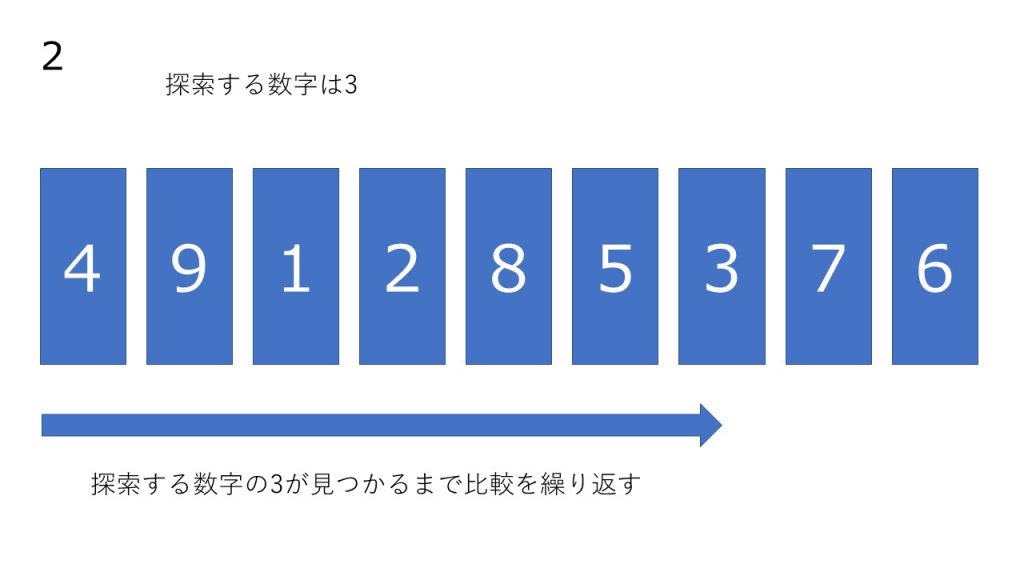
- 配列の先頭の文字を調べます。数値を比較し、一致すれば、探索を終了します。一致しなければ 1 つ次の数字を調べます。
- 順次、数値を比較し、一致すれば、探索を終了します。一致しなければ 1 つ次の数字を調べます。
コード
とても単純なコードですが線形探索のコードを C#で書きました。
線形探索で返却するものは何番目の要素かというところを終着点としました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
using System; using System.Collections.Generic; namespace Algorithm { class Program { static void Main(string[] args) { var list = new List<int> { 2, 4, 9, 1, 8, 5, 3, 7, 6 }; var array = list.ToArray(); Console.WriteLine("{" + string.Join(",", array) + "}"); Console.WriteLine("線形探索の結果は： index = " + Search(array, 1)); } private static int Search(int[] data, int target) { var noValue = -1; for (var i = 0; i < data.Length; i++) { if (data[i] == target) { // 添字を返す return i; } } return noValue; } } } |
二分探索
概要
二分探索はソートされた配列に対して行なう探索です。
線形探索よりも効率の良い探索を行えますが、データが整列されている必要があるため利用できるシーンは限られます。
処理
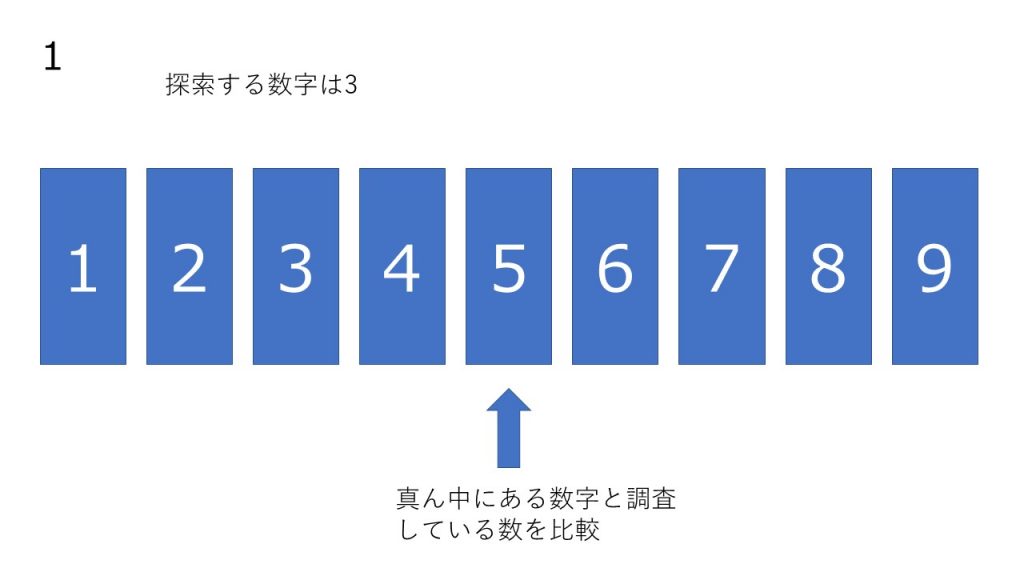
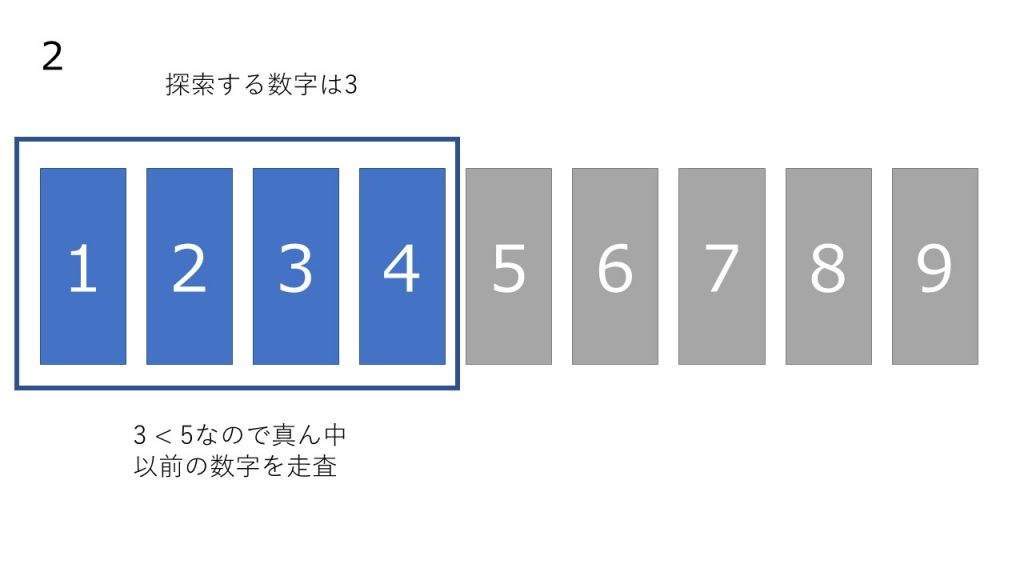
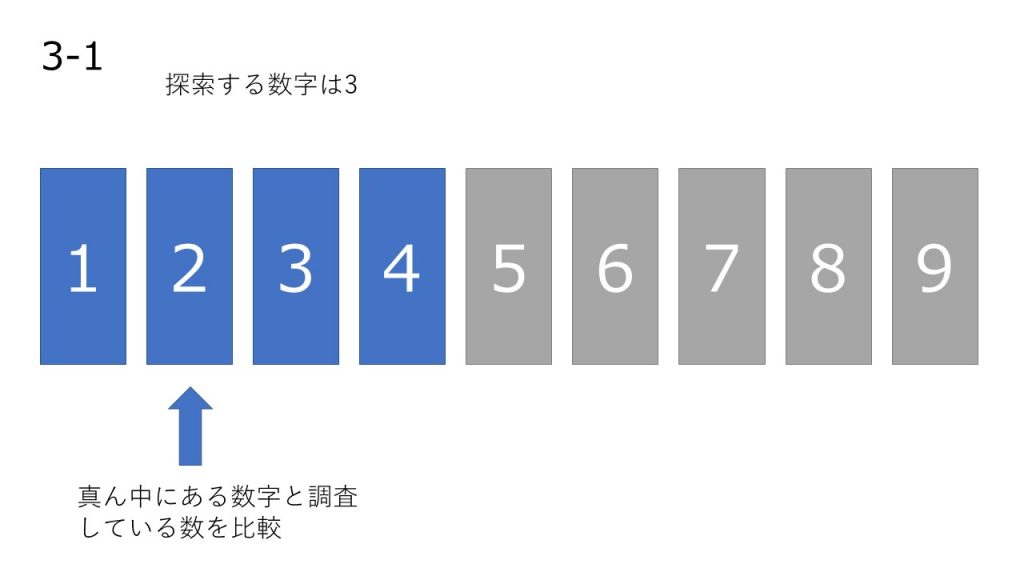
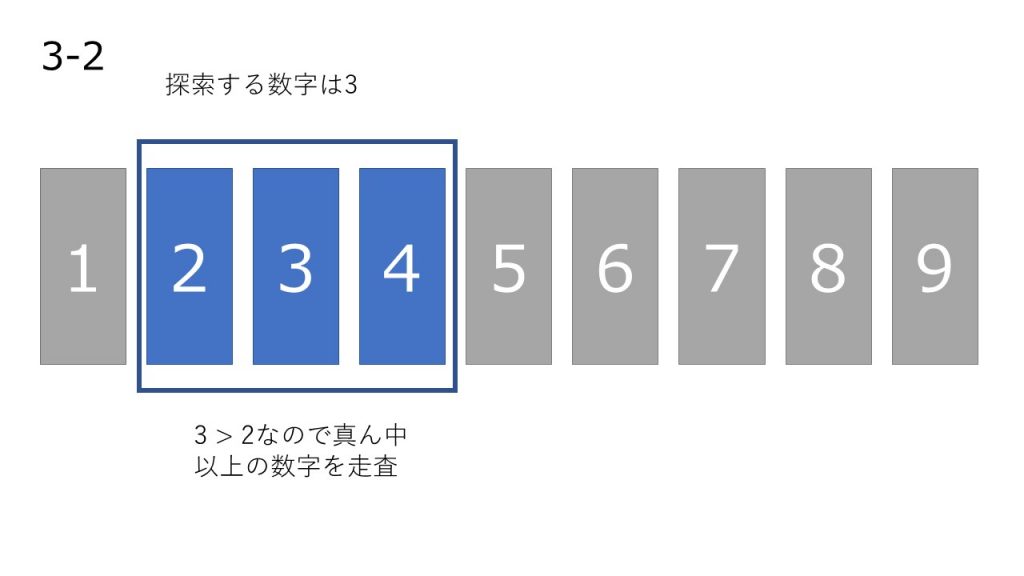
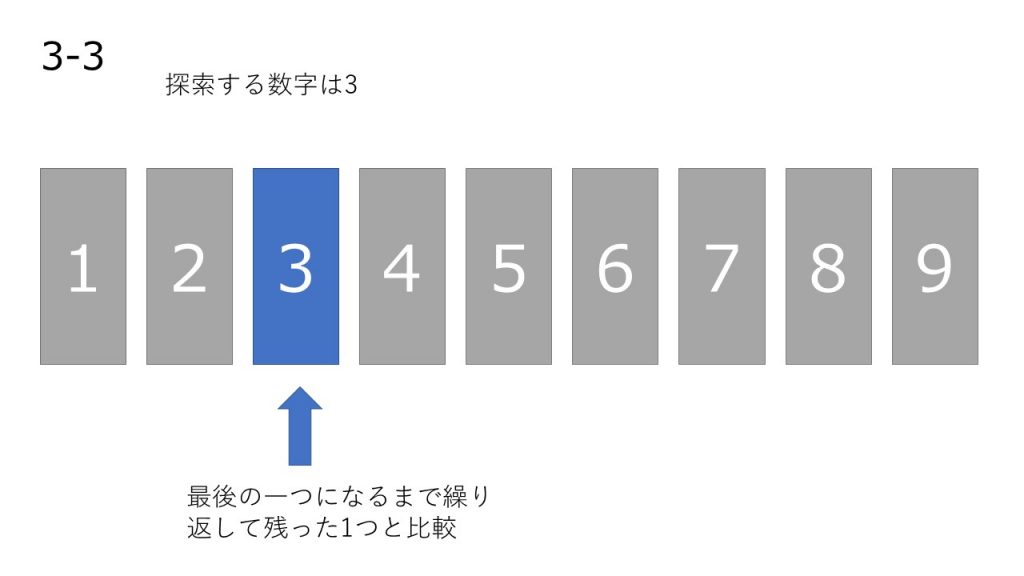
- 配列の真ん中にある数を調べ探索する数と比較する。
- 比較した結果、探索する数の方が大きい場合は右を、小さい場合は左を新しい配列と考える
- 1,2 の処理を要素が 1 つになるまで繰り返し、最後に残った 1 つ探索する数を比較する
オーダー
半分ずつ探索していくので、 
になります。
なぜ半分ずつ処理すると になるのかは第 4 回のマージソートで確認いただけると思います。
整列されたものを探索すると になるのですが、バラバラな配列の場合はソートしてから探索することになります。
前回まででソートのオーダーも見ていきましたが、最良のものでも 
になるので、全体の処理時間も となります(参照 第 4 回 クイックソート)。
それだと線形検索より遅くなりますので、状況に応じて使い分けてください。
コード
二分探索のコードを C#で書きました。
探索する数が大きいか小さいか比較して、前後にグループ分けして再帰的に処理を行いました。
Program.cs
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
using System; using System.Collections.Generic; using Algorithm.Search; namespace Algorithm { class Program { static void Main(string[] args) { var list = new List<int>(); // 1～100の数字をバラバラに配列に入れる for (var i = 1; i < 101; i++) { list.Add(i); } var array = list.ToArray(); Console.WriteLine("{" + string.Join(",", array) + "}"); Console.WriteLine("二分探索の結果は： index = " + BinarySearch.Search(array, i)); } } } |
BinarySearch.cs
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
namespace Algorithm.Search { public static class BinarySearch { public static int Search(int[] data, int target) { if (data.Length < 1) { return -1; } return Recursive(data, 0, data.Length - 1, target); } private static int Recursive(int[] data, int first, int last, int target) { // 最後の一つとtargetが等しいか確認。違っていたら-1を返す if (first == last) { return data[first] == target ? first : -1; } var center = (first + last) / 2; // 再帰的に走査 return data[center] >= target ? Recursive(data, first, center, target) : Recursive(data, center + 1, last, target); } } } |
おわりに
今回は探索のアルゴリズムを考えました。
探索のアルゴリズムも色々な方法がありますので、そのバラエティに富んだ方法を紹介していけたらと思います。
ソートと同様に、探索の関数も各言語で用意されていると思いますが、その中身を考えることで適切な関数を使えたり、適切な処理を書けるようになると思います。