毎月アルゴリズム – 第5回 –

はじめに

こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第 5 回目です。
前回はシェルソート、マージソート、クイックソートのアルゴリズムを見ていきました。
今回ヒープソートを紹介して、ソートに関するアルゴリズムは終了としようと思います。

データ構造

第 3 回までで、線形のデータ構造を説明しました。
今回はグラフデータ構造と言われる、ヒープと二分探索木に関して解説していきたいと思います。

ヒープ

ヒープは優先度付きキューの実装の一つです。
優先度付きキューは集合 (set) を扱うデータ型で、集合に含まれる要素が何らかの優先度 (priority) 順に取り出されるという特徴を持っています。
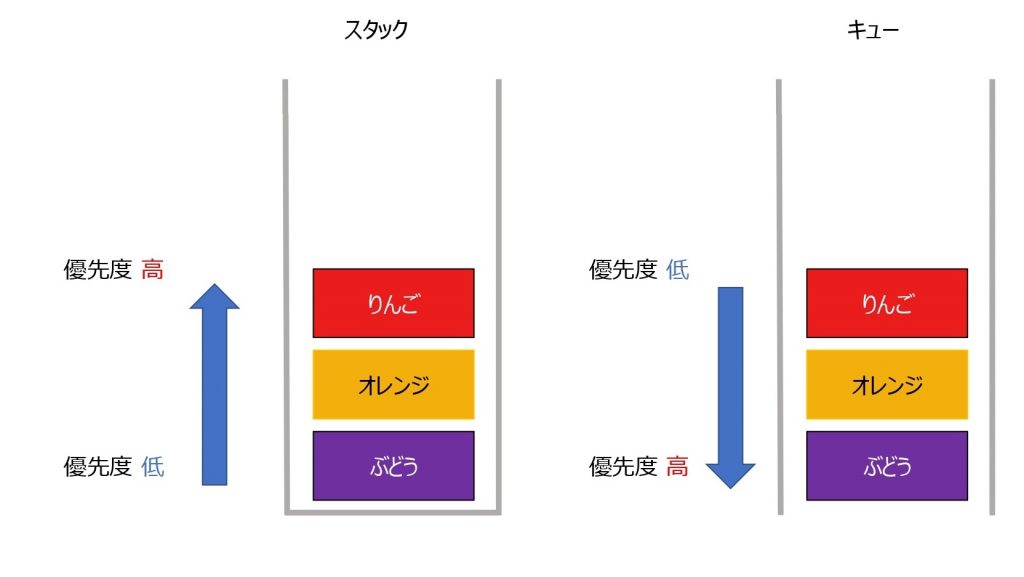
キューとスタックに関しては、以前の記事で説明しました。
キューとスタックも優先度付きキューの 1 種と考えることができます。
(FIFO と LIFO がそれに当たります)

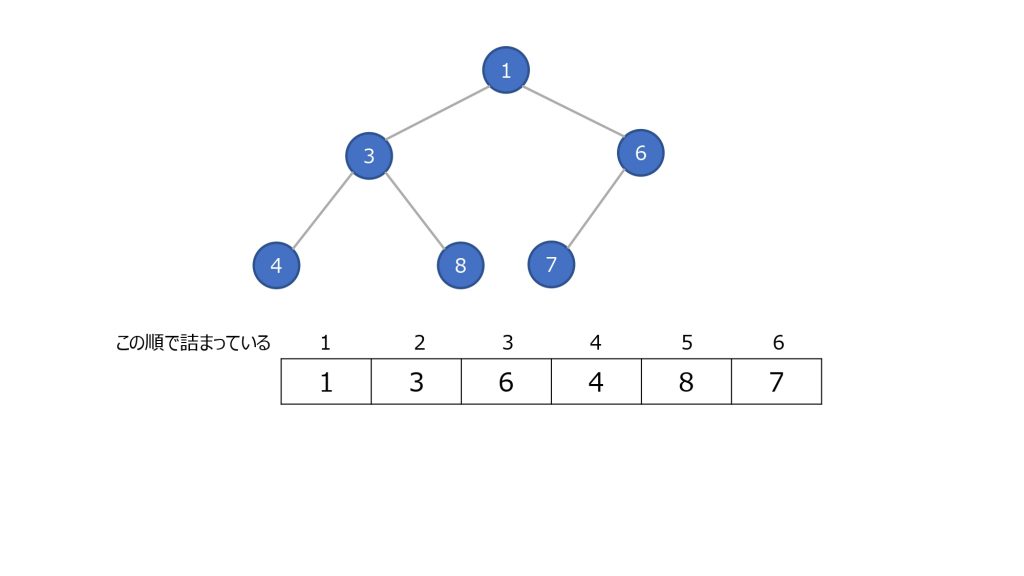
データ構造の特徴は以下です

分岐点の頂点を「ノード」と呼ぶ
ノードは子ノードを 2 つまで持てる
頂点のノードの値は子のノードよりも小さい値をとる
ノードは上詰め、同じ段では左詰めになる

構造上、一番頂点のノードは常に最小の値となります。

探索

ヒープ構造では子要素間の大小関係に制約が無いため、目的とする要素が見つかるまで全要素を順に調べる必要がある。
したがって、任意のデータを探索する必要がある場合にヒープ構造を使うことは勧められない。

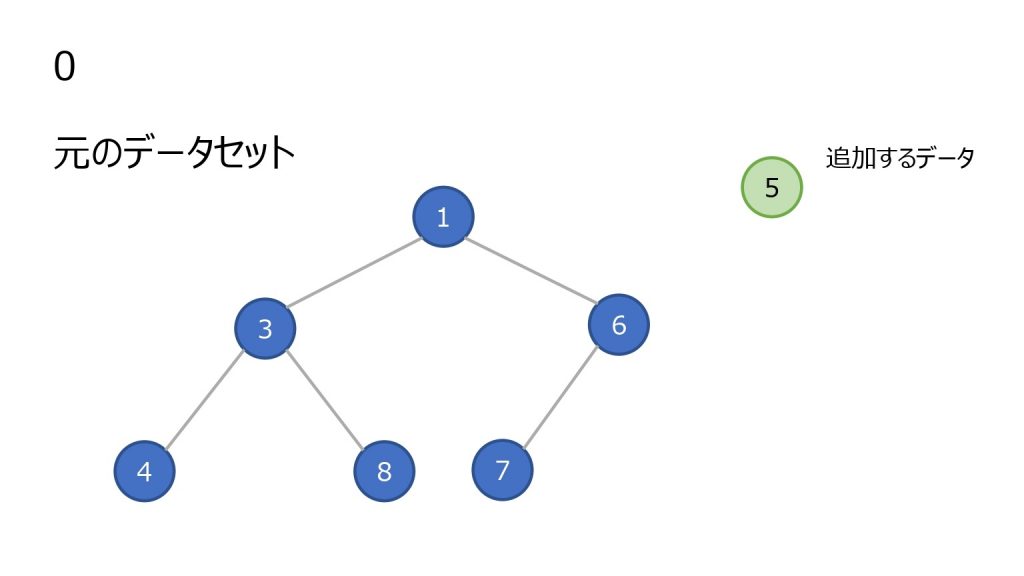
追加

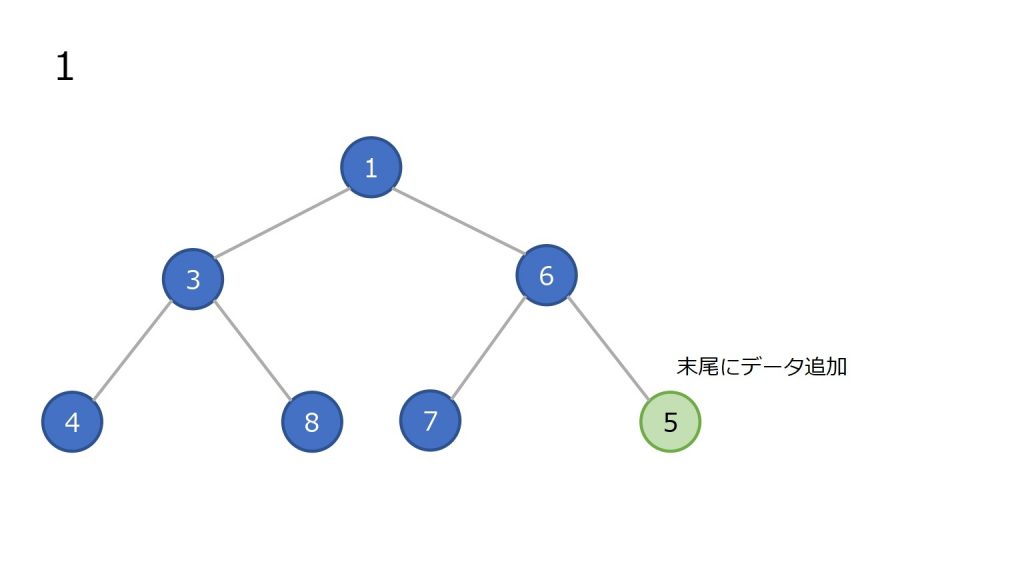
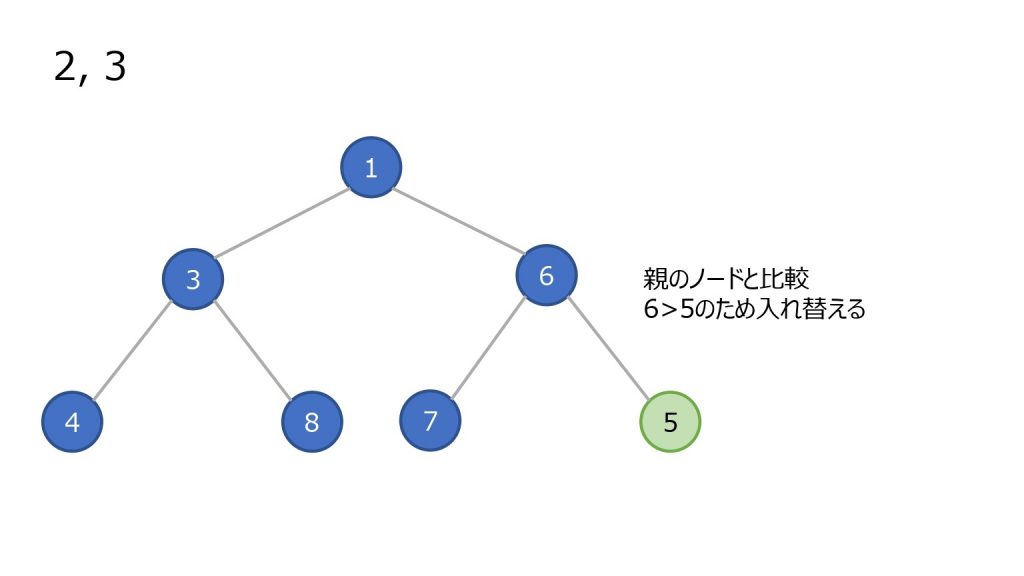
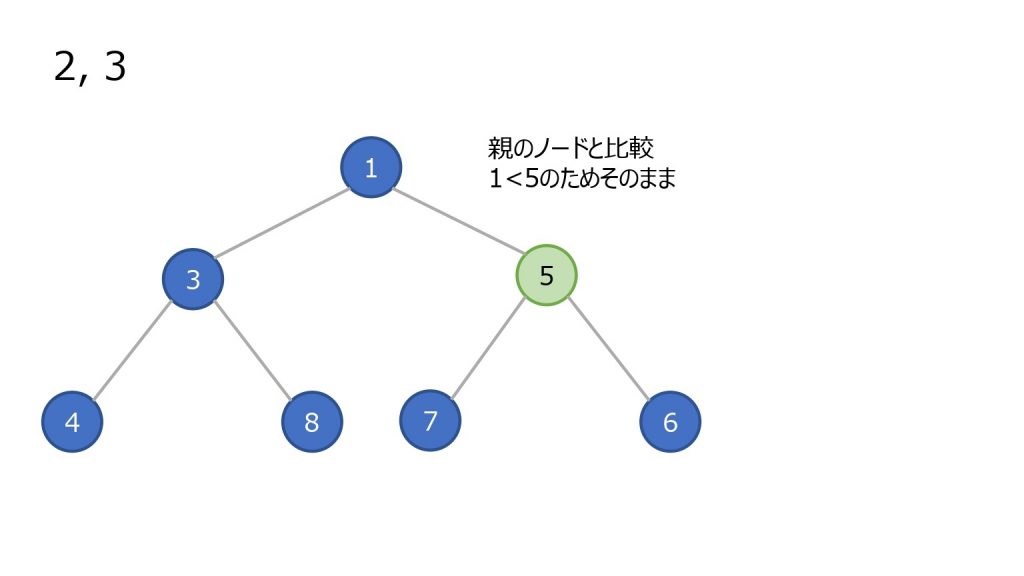
末尾(ツリーで見ると一番右下)にノードを追加
親ノードと比較し、親ノード以上の数値ならそのまま
親ノードの方が大きければ親子を入れ替え、2 を繰り返す

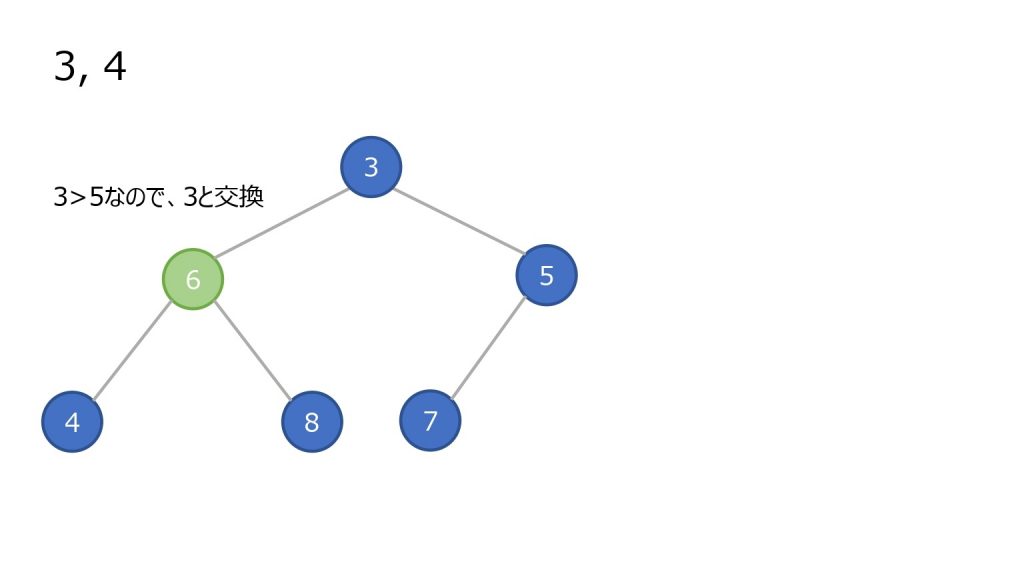
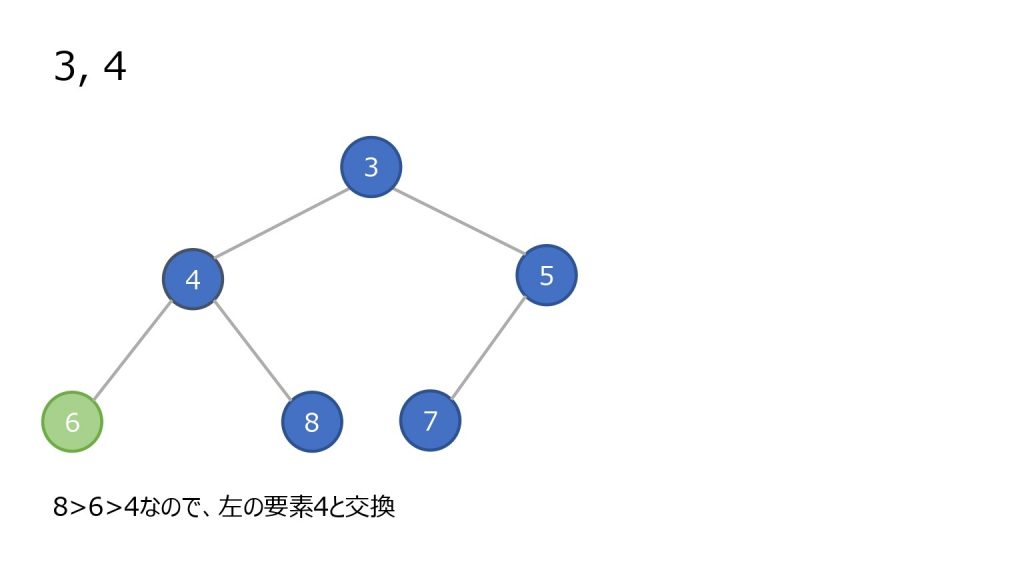
取り出し

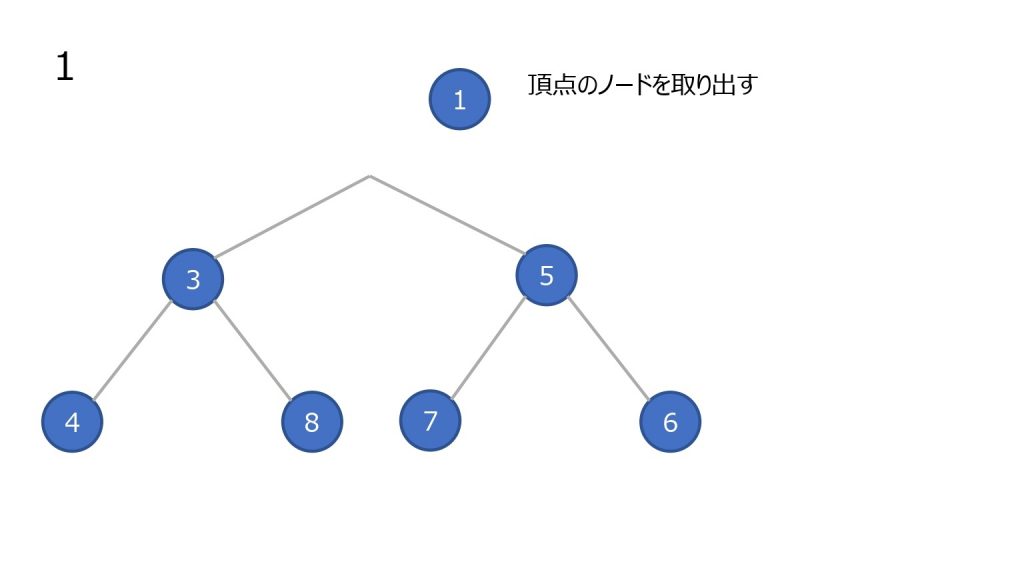
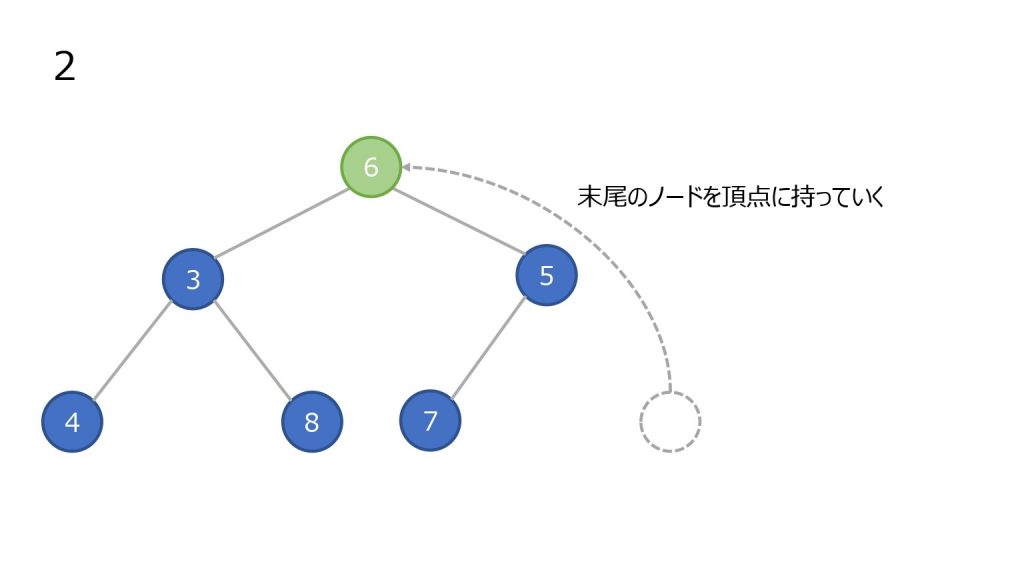
頂点のノードを取り出す(最小値)
末尾(ツリーで見ると一番右下)のノードを頂点に持っていく
そのノードと子ノードと比較する。子ノードが存在しないかすべての子ノードの比較結果が比較している数字以上なら終了
小さい方の子ノードと元のノードを入れ替えて、更に子ノードと比較をする(3 を繰り返す)

再構築にかかる時間

追加したり取り出したりする場合、ノードの順番を入れ替える作業をヒープの再構築と呼びます。
(ツリーを再構築しているように見えますよね)
データ数が $n$ とすると、ツリーの高さは高々 $logn$ となります。

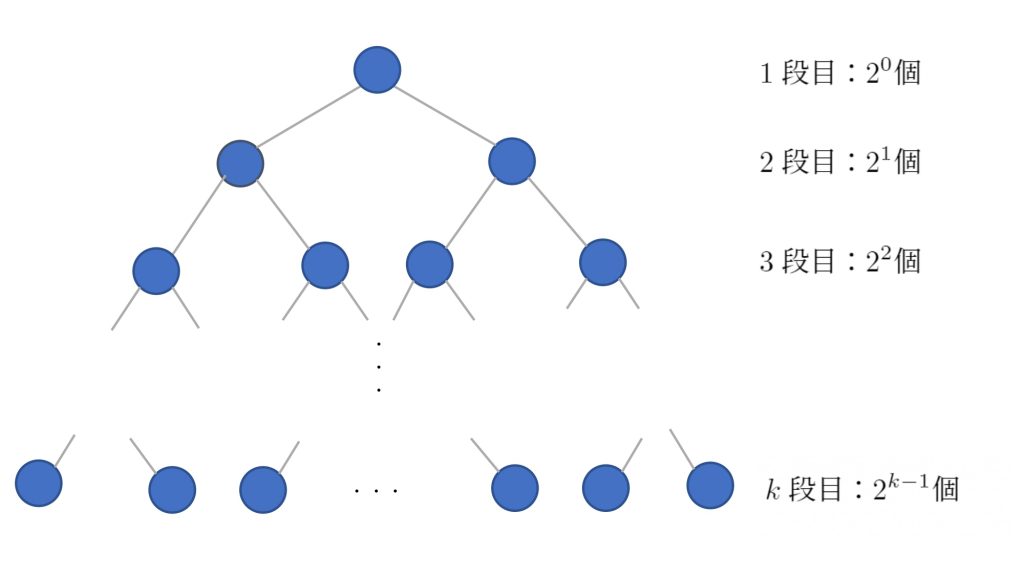
上図より、
$2^0 + 2^1 + 2^2 + \cdots + 2^{k-1} = n$
$\frac{2^k - 1}{2 - 1} = n$
$2^k = n + 1$
$k = log(n + 1)$
となり、ツリーにフルでノードが詰まっていた場合でも高さは $log(n+1)$ なので、高さは高々 $logn$ としても大丈夫です。
高さが $logn$ になるので、追加、取り出しを行ったときの交換は $logn$ 回起こるので、再構築にかかる時間は $O(logn)$ となります。

まとめ

ヒープは優先度付きキューの一種
常に先頭ノードに最小値が格納されているため、最小値の取得は $O(1)$
追加、取出後の再構築にかかる時間は $O(logn)$
ヒープはデータの探索には向かない構造である

二分探索木

二分探索木はグラフの木構造を利用しています。
以下 2 つの特徴を持ちます。

すべてのノードはそのノードの左部分木に含まれるどの数字よりも大きくなる
すべてのノードはその右部分木よりも小さくなる

意味不明だと思いますので、例によって図を使って説明します。
二分探索木において、どのノードも必ず左の子ノード < 親のノード < 右の子ノードの関係になっています。
不等号には等号をどちらか片方につけても問題はありません。(今回の記事ではわかりやすさのため省略しています)

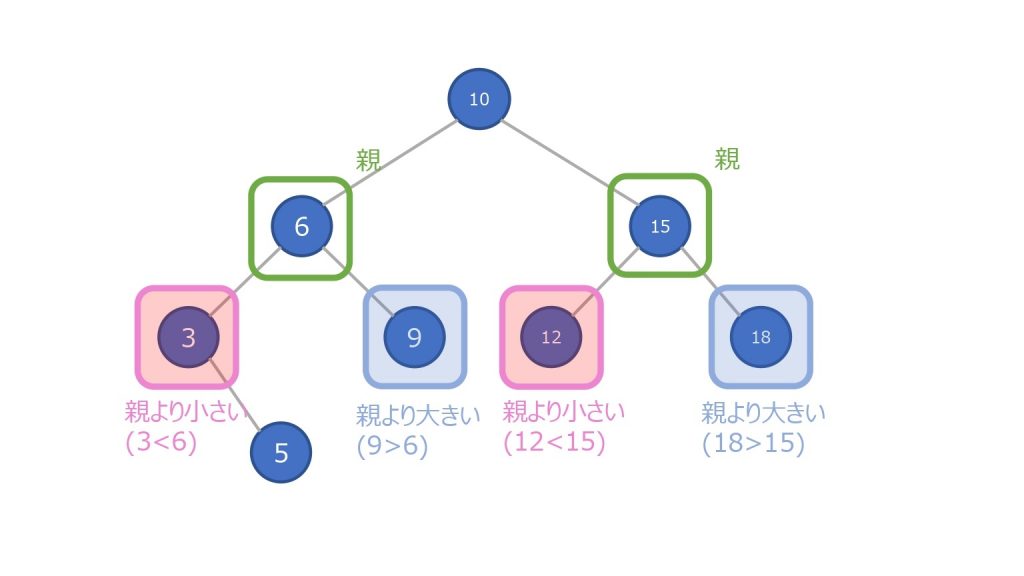
更に、ノードだけではなく、そのノードにある配下も全て親ノードより大きい、または小さいという性質があります。
左部分木 < 親のノード < 右部分木

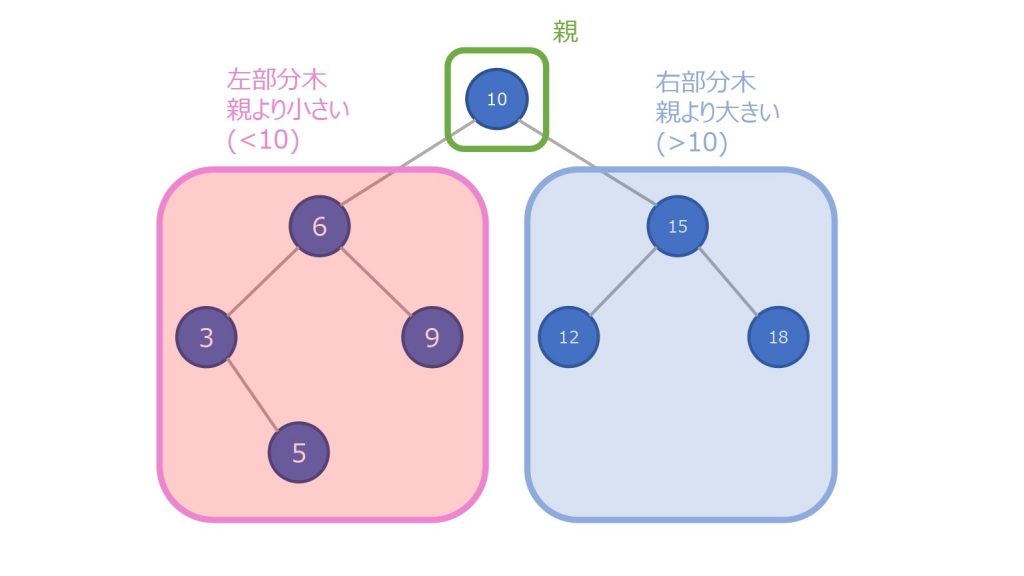
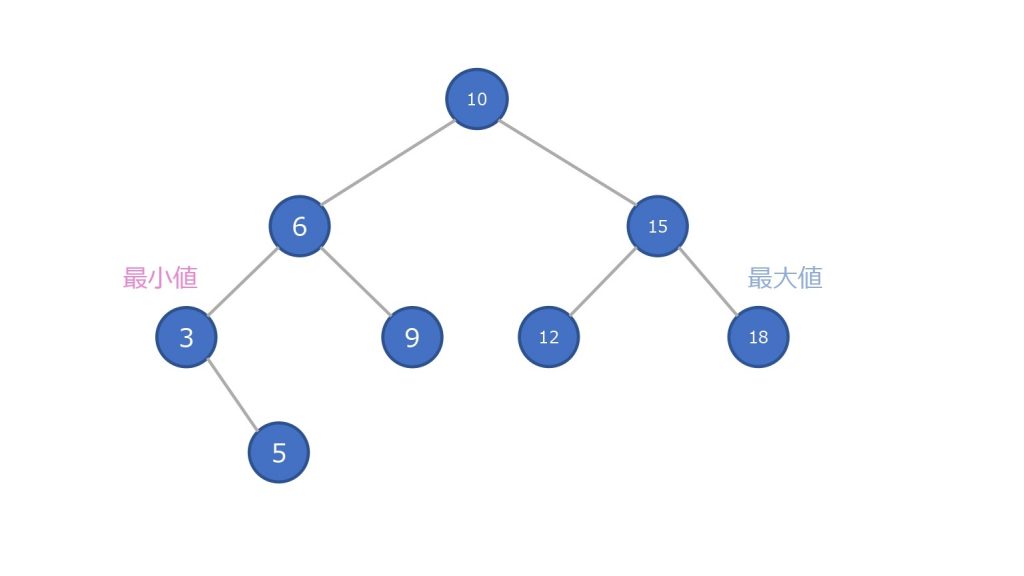
その性質により、最小値は一番左にあるノード、最大値は一番右にあるノードということが決定します。

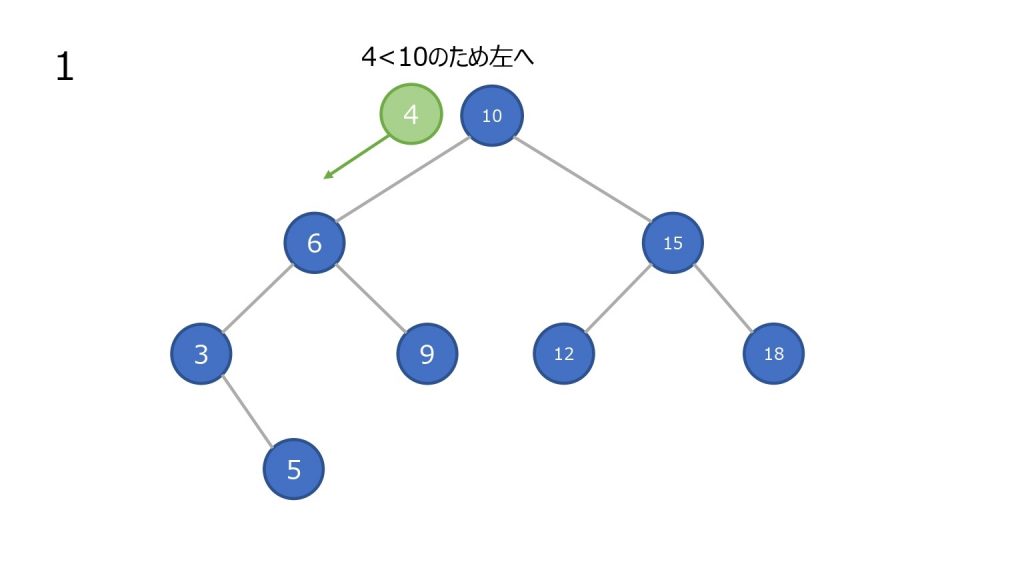
追加

最上部のノードと比較して小さければ左の子ノードに進む、大きければ右の子ノードに進む
ノードが存在していれば、そのノードと比較して小さければ左の子ノードに進む、大きければ右の子ノードに進む
2 でノードが存在しないところまで到達すれば、新しいノードとしてその要素を加える

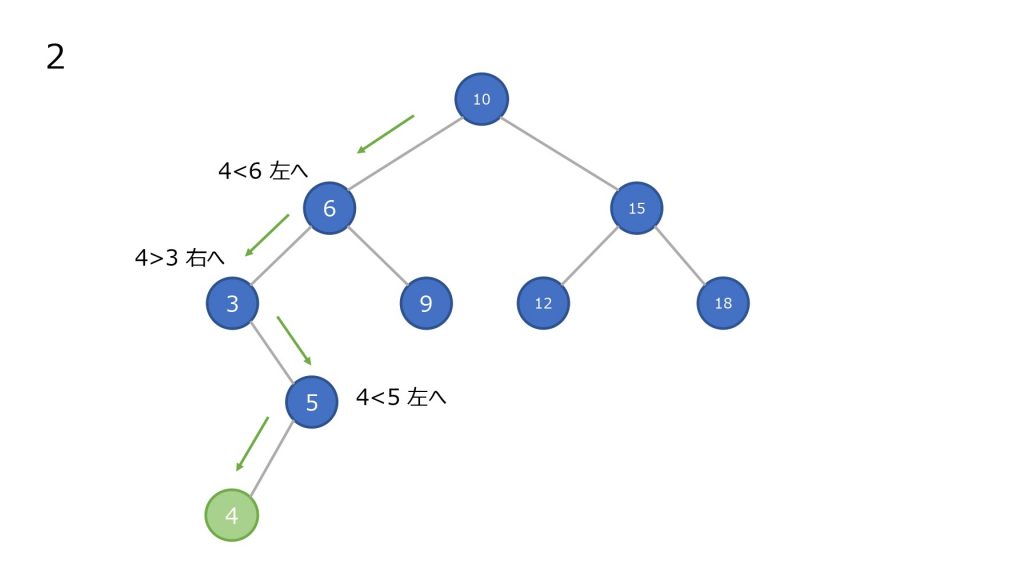
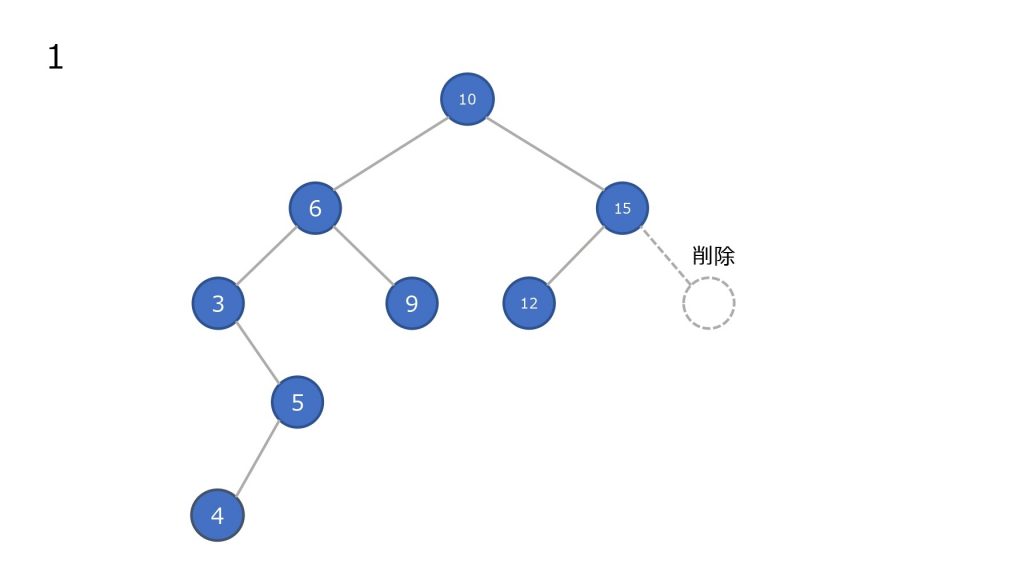
削除

子ノードが無いノードを削除した場合

ノードを削除

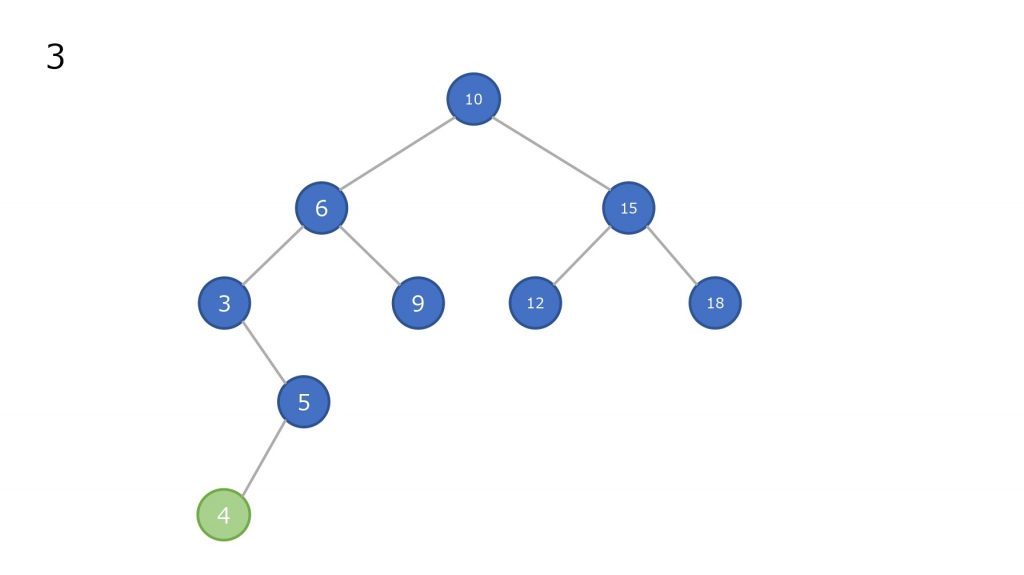
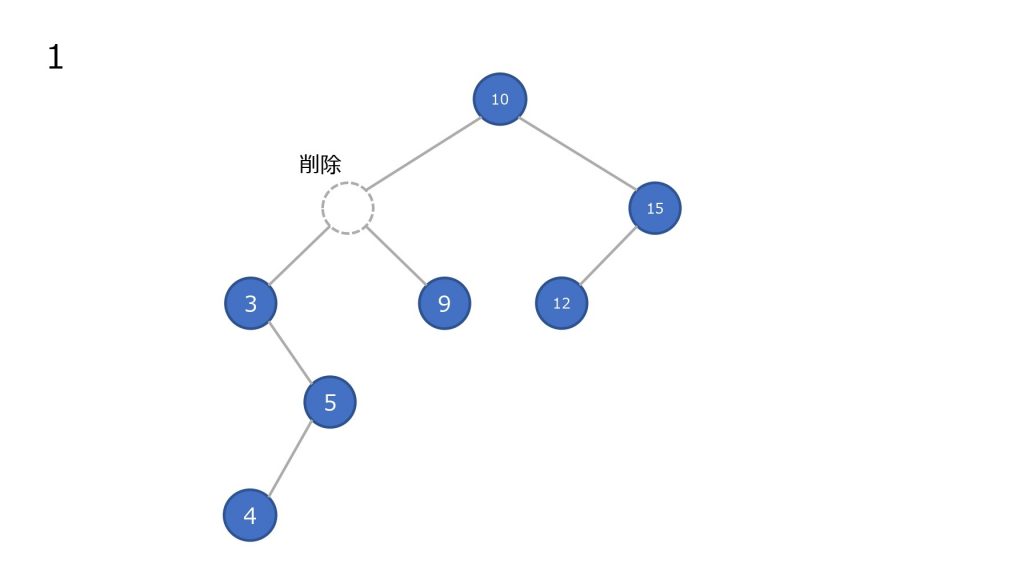
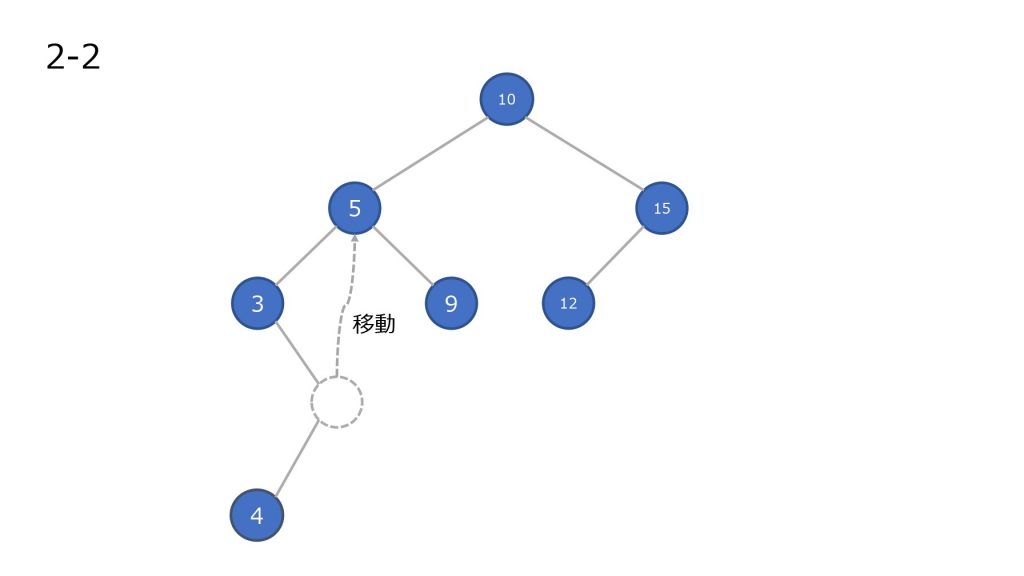
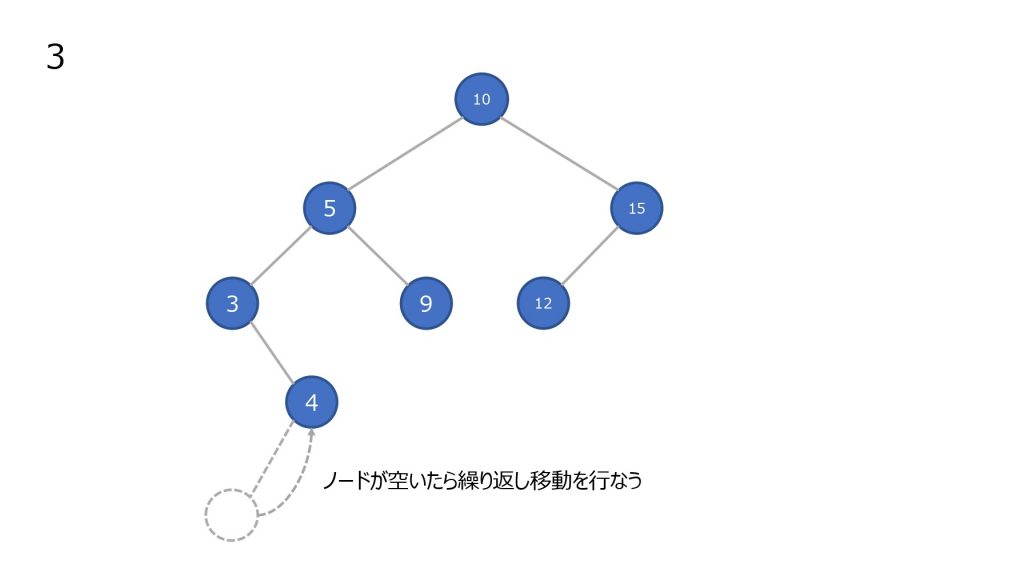
子ノードを持つノードを削除した場合

ノードを削除
削除したノードの左部分木の最大値を持ってきて移動させる
2 で左部分木に値がなくなるまで繰り返す

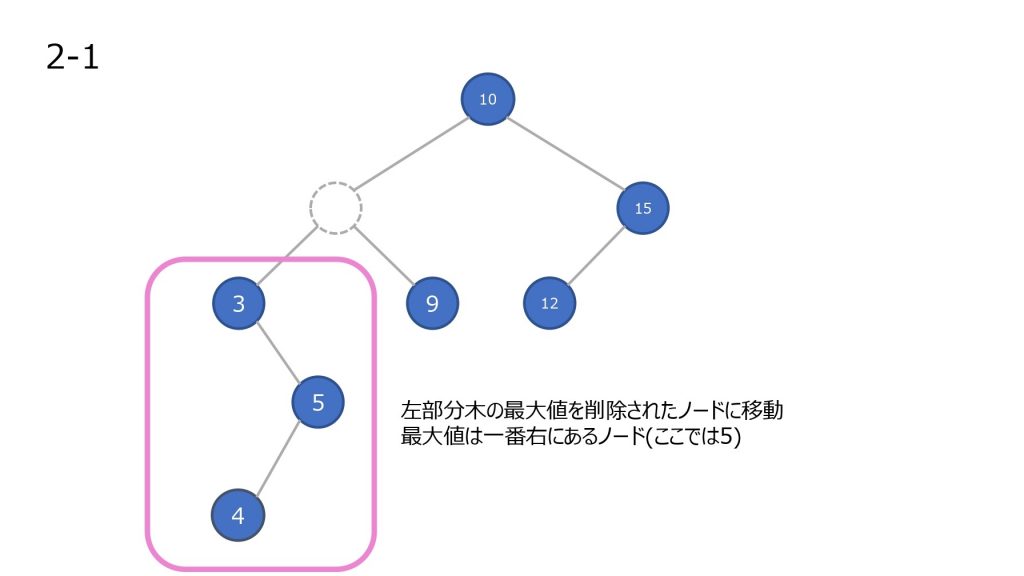
探索

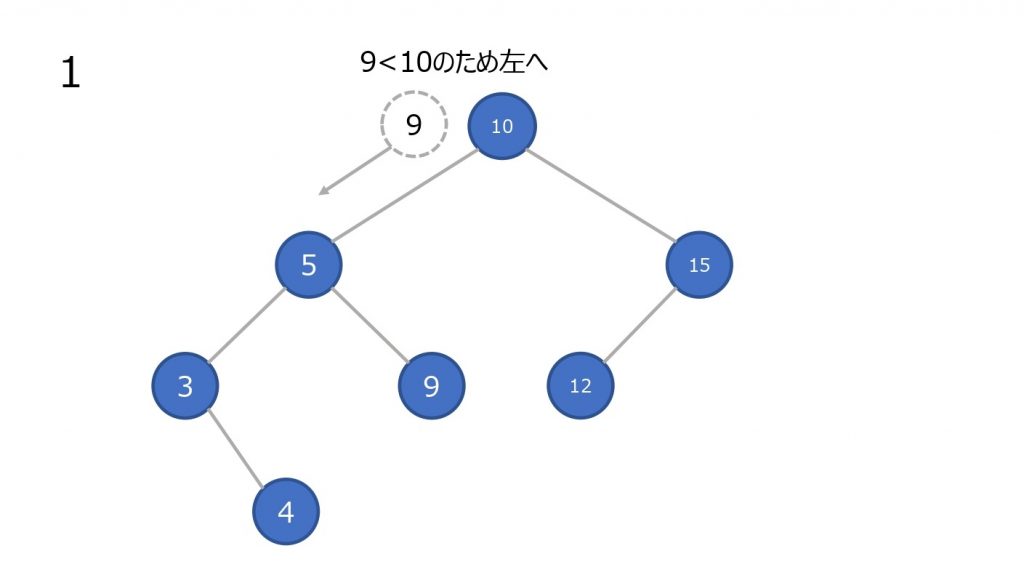
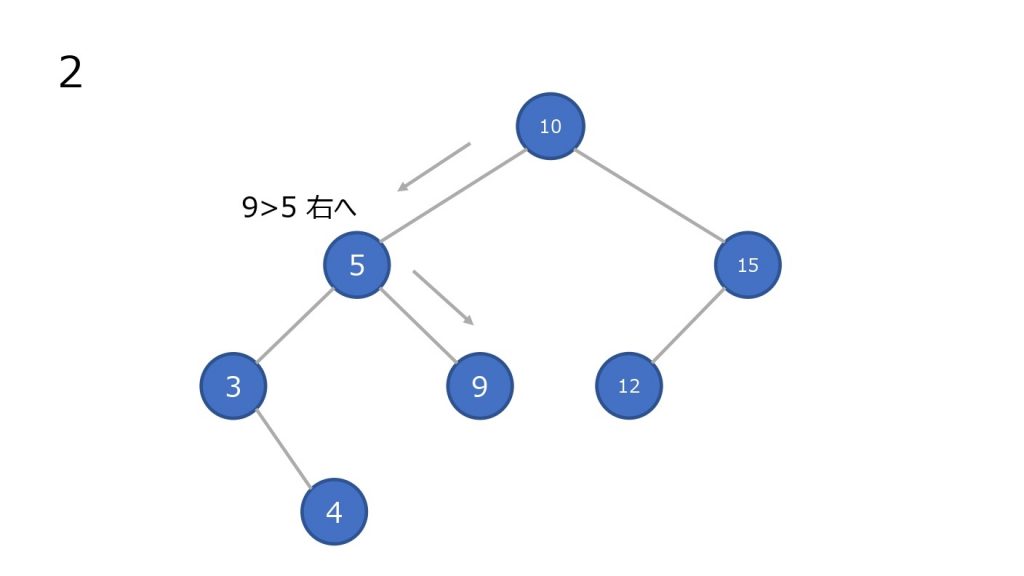
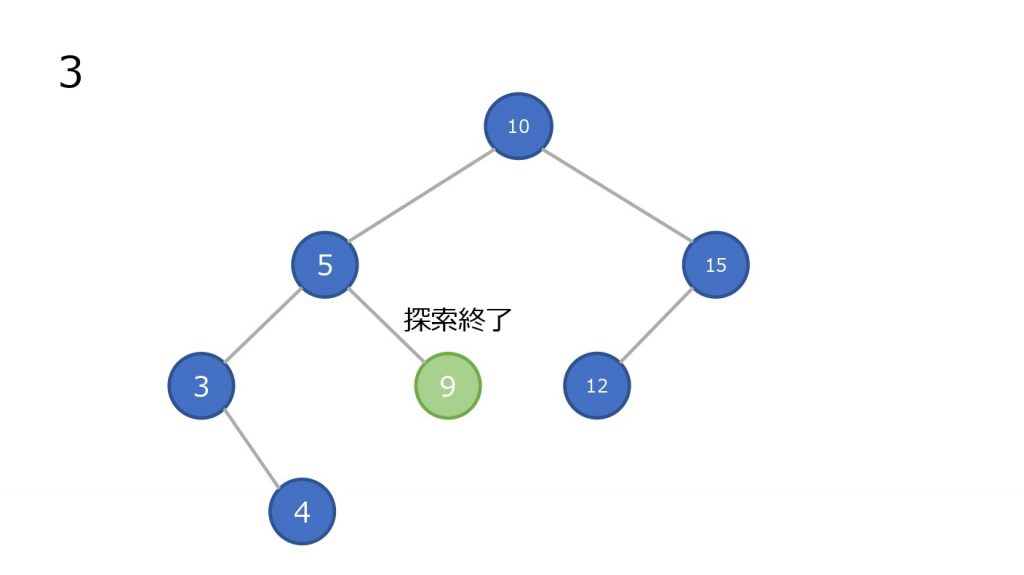
最上部のノードと比較して小さければ左の子ノードに進む、大きければ右の子ノードに進む。一致していれば終了
子ノードと比較して小さければ左の子ノードに進む、大きければ右の子ノードに進む
2 を一致するノードが見つかるまで行なう

計算量

追加、探索において、計算量は高さ分回数を比較することがおわかりいただけると思います。
ヒープのときに見たようにバランス良く木が構成されている場合、 $O(logn)$ で計算可能となりますが、左右のどちらかに偏ってしまう場合、1 直線に並ぶことになり、 $O(n)$ のコストがかかってしまいます。

まとめ

二分探索木は木構造をとっている
必ず左の子ノード < 親のノード < 右の子ノードの関係になっている
必ず左部分木 < 親のノード < 右部分木の関係になっている
追加、探索の最良計算量は $O(logn)$ , 最悪計算量は $O(n)$

アルゴリズムを考えてみる

本日は以下のソートに関してアルゴリズムを考えていきます。

ヒープソート

ヒープソート

概要

ヒープソートはデータ構造のヒープを利用してソートを行う方法です。
ヒープの項でほぼ説明は完了しているのですが、ヒープの構造では常に頂点のノードが最小値となるように構築しているので、それを取得し続けることでソートを完了します。

オーダー

ヒープソートははじめにヒープを構成する必要があり、ヒープを構築するのに $O(logn)$ という話をしました。
$n$ 個の要素を繰り返し構築するので、 $O(nlogn)$ となります。
その後、各ラウンドで最大の数を取り出して、再構築する手順を挟むので、ソートにかかる時間は $O(nlogn)$ です。
それらを総合することで、ヒープソートの計算時間は全体で $O(nlogn)$ です。

処理

処理はヒープソートの構築に記載したとおりです。
そのため本項は省略します。

コード

いつもどおりヒープソートのコードを C#で書きました。
Program.cs

using System;
using System.Collections.Generic;
using System.Linq;
using Algorithm.Sort;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();

      // 1～100の数字をバラバラに配列に入れる
      for (var i = 1; i < 101; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();
      Console.WriteLine("{" + string.Join(",", HeapSort.Sort(array)) + "}");
    }
  }
}

using System;

using System.Collections.Generic;

using System.Linq;

using Algorithm.Sort;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～100の数字をバラバラに配列に入れる

for (var i = 1; i < 101; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", HeapSort.Sort(array)) + "}");

}

HeapSort.cs

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm.Sort
{
  public static class HeapSort
  {
    public static int[] Sort(int[] arr)
    {
      var heap = new Heap(arr);
      var length = heap.Size;
      var list = new List<int>();

      for (int i = 0; i < length; i++)
      {
        list.Add(heap.Pop());
      }
      return list.ToArray();
    }

    private class Heap
    {
      private List<int> _tree;

      public int Size => this._tree.Count;

      public Heap(int[] items)
          => this.Build(items);

      /// <summary>
      /// ヒープ作成
      /// </summary>
      public void Build(int[] items)
      {
        var tree = items;

        for (int i = 0; i < tree.Length; i++)
        {
          // 挿入するデータの添字
          var n = i;

          while (n > 0)
          {
            // 自分の親は(n - 1) / 2で取得する
            var parent = (n - 1) / 2;

            // 親より子が大きければ交換
            if (tree[parent] > tree[n])
            {
              var tmp = tree[parent];
              tree[parent] = tree[n];
              tree[n] = tmp;
            }

            // 繰り返し親を見て構築
            n = parent;
          }
        }
        this._tree = tree.ToList();
      }

      /// <summary>
      /// 最小値を取得
      /// </summary>
      /// <returns></returns>
      public int Pop()
      {
        if (this._tree.Count == 0)
        {
          throw new Exception("要素が0のためPopできない");
        }

        // 返す要素は先頭の値
        var root = this._tree[0];

        // 末尾を先頭に持ってくる
        this._tree[0] = this._tree.Last();
        this._tree.RemoveAt(this._tree.Count - 1);

        this.Heapify(0);

        return root;
      }

      /// <summary>
      /// 特定のノード以下を走査して、再構築する
      /// </summary>
      private void Heapify(int index)
      {
        var tree = this._tree.ToArray();

        // ヒープの再構築
        var i = index;

        // 子が存在する限りループする
        while (0 < 2 * i + 1 && 2 * i + 1 < tree.Length)
        {
          // 左詰めで入っているのでleftChildは確実に存在するが、rightChildは存在しない可能性がある
          var leftChild = 2 * i + 1;
          var rightChild = (2 * i + 2 < tree.Length) ? (2 * i + 2) : -1;

          // 子の小さい方と比較する
          var target = rightChild != -1 && tree[leftChild] < tree[rightChild]
            ? leftChild
            : rightChild;

          // もし子の方が小さければ交換する
          if (target != -1 && tree[i] > tree[target])
          {
            var tmp = tree[i];
            tree[i] = tree[target];
            tree[target] = tmp;
          }
          i = target;
        }

        this._tree = tree.ToList();
      }
    }
  }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm.Sort

{

public static class HeapSort

{

public static int[] Sort(int[] arr)

{

var heap = new Heap(arr);

var length = heap.Size;

var list = new List<int>();

for (int i = 0; i < length; i++)

{

list.Add(heap.Pop());

}

return list.ToArray();

}

private class Heap

{

private List<int> _tree;

public int Size => this._tree.Count;

public Heap(int[] items)

=> this.Build(items);

/// <summary>

/// ヒープ作成

/// </summary>

public void Build(int[] items)

{

var tree = items;

for (int i = 0; i < tree.Length; i++)

{

// 挿入するデータの添字

var n = i;

while (n > 0)

{

// 自分の親は(n - 1) / 2で取得する

var parent = (n - 1) / 2;

// 親より子が大きければ交換

if (tree[parent] > tree[n])

{

var tmp = tree[parent];

tree[parent] = tree[n];

tree[n] = tmp;

}

// 繰り返し親を見て構築

n = parent;

}

this._tree = tree.ToList();

}

/// <summary>

/// 最小値を取得

/// </summary>

/// <returns></returns>

public int Pop()

{

if (this._tree.Count == 0)

{

throw new Exception("要素が0のためPopできない");

}

// 返す要素は先頭の値

var root = this._tree[0];

// 末尾を先頭に持ってくる

this._tree[0] = this._tree.Last();

this._tree.RemoveAt(this._tree.Count - 1);

this.Heapify(0);

return root;

}

/// <summary>

/// 特定のノード以下を走査して、再構築する

/// </summary>

private void Heapify(int index)

{

var tree = this._tree.ToArray();

// ヒープの再構築

var i = index;

// 子が存在する限りループする

while (0 < 2 * i + 1 && 2 * i + 1 < tree.Length)

{

// 左詰めで入っているのでleftChildは確実に存在するが、rightChildは存在しない可能性がある

var leftChild = 2 * i + 1;

var rightChild = (2 * i + 2 < tree.Length) ? (2 * i + 2) : -1;

// 子の小さい方と比較する

var target = rightChild != -1 && tree[leftChild] < tree[rightChild]

? leftChild

: rightChild;

// もし子の方が小さければ交換する

if (target != -1 && tree[i] > tree[target])

{

var tmp = tree[i];

tree[i] = tree[target];

tree[target] = tmp;

}

i = target;

}

this._tree = tree.ToList();

}

おわりに

今回でソートに関するアルゴリズムは終了です。
次回からは探索系のアルゴリズムを考えていく予定です。
よろしければまたご覧になってください。

第0回 (初歩的な数学のアルゴリズムを考えてみよう)
第1回
 第2回
 第3回
 第4回

Blazor WebAssembly で MVVM を実現する(第2回)

縦持ちを横持ちにして集計する

毎月アルゴリズム – 第5回 –

はじめに

データ構造

ヒープ

探索

追加

取り出し

再構築にかかる時間

まとめ

二分探索木

追加

削除

子ノードが無いノードを削除した場合

子ノードを持つノードを削除した場合

探索

計算量

まとめ

アルゴリズムを考えてみる

ヒープソート

概要

オーダー

処理

コード

おわりに

最近の記事

顔認証（DeepFace vs GPT4o）

時系列解析再訪

πの新しい公式

中心極限定理

DBSCANを用いたクラスタリング

レイアウト解析

毎月アルゴリズム – 第6回 –

【モンテカルロ法】プログラミングで円周率を求める方法

【モンテカルロ法】ビュフォンの針の問題

初歩的な数学のアルゴリズムを考えてみよう

毎月アルゴリズム – 第3回 –

毎月アルゴリズム – 第2回 –

Google Vision APIでOCR

アーカイブ

カテゴリー