毎月アルゴリズム – 第4回 –

はじめに

こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第4回目です。
前回はより多く種類のデータ構造を見ていきました。
今回でデータ構造をすべて話しきろうと思いましたが、今までデータ構造の話ばかりだったのでアルゴリズム多めの回にしようかなと考えまして、今回はアルゴリズムのみを考えていこうと思います。
前回までのデータ構造で、一応線形のデータ構造は考えましたので、次回以降でグラフデータの構造を考えていきたいと思います。

アルゴリズムを考えてみる

本日は以下のソートに関してアルゴリズムを考えていきます。

シェルソート
マージソート
クイックソート

シェルソート

概要

シェルソートは改良挿入ソートとも呼ばれます。

前回を思い出していただきたいのですが、挿入ソートは最悪計算量が $O(n^2)$ だったのに対して、最良計算量は $O(n)$ でした。
そのため、挿入ソートは「整列されたデータに対しては高速」、「あまり整列されていないデータに対しては低速」という特長があると言えます。

適当な間隔を開けて飛び飛びのデータ列に対して予めソートをして、その数列に対して挿入ソートを適用すれば高速になると考えられたのがこのシェルソートです。

処理

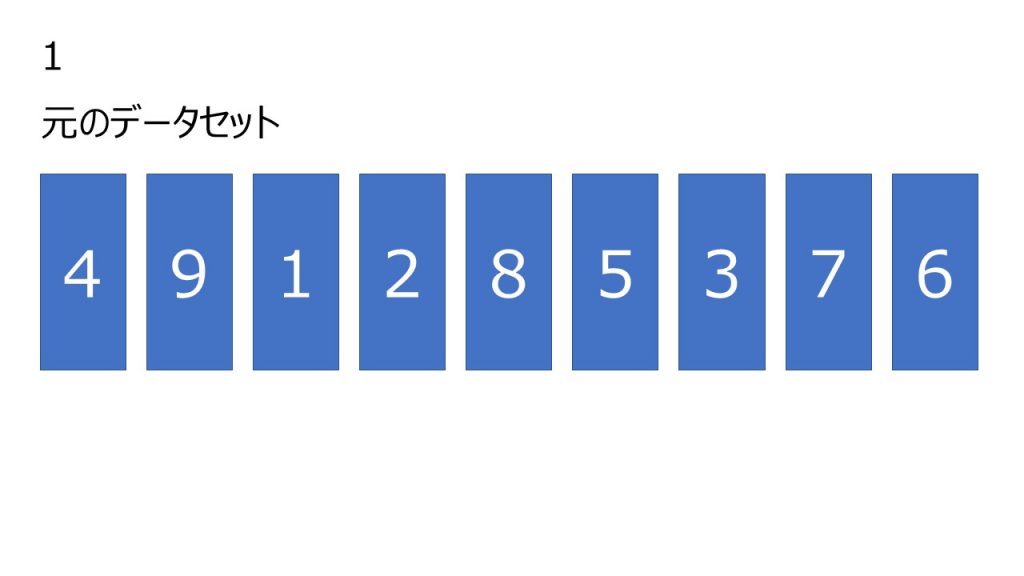
元データを用意する
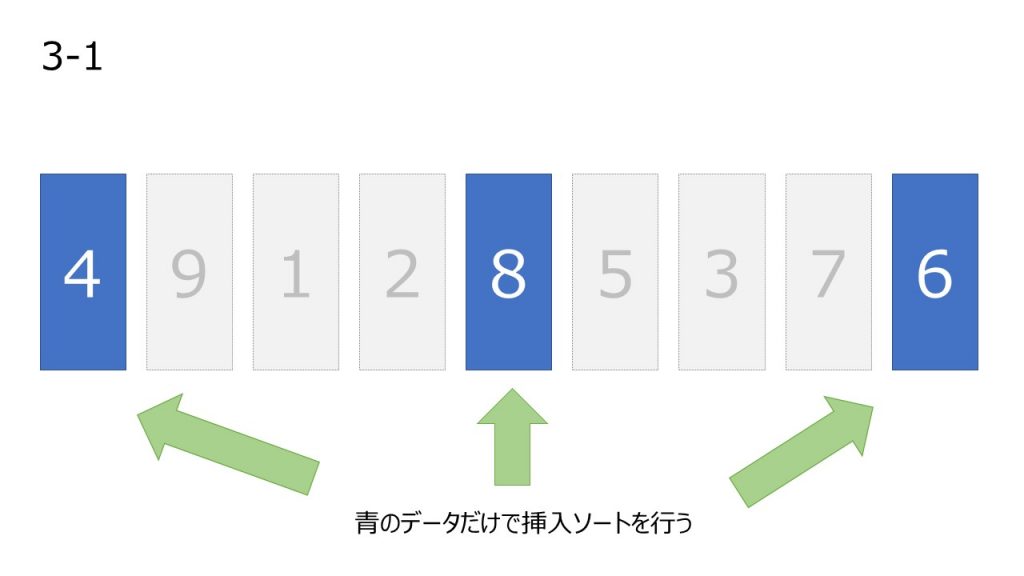
適当な間隔 h を決定する。(今回は4とする)
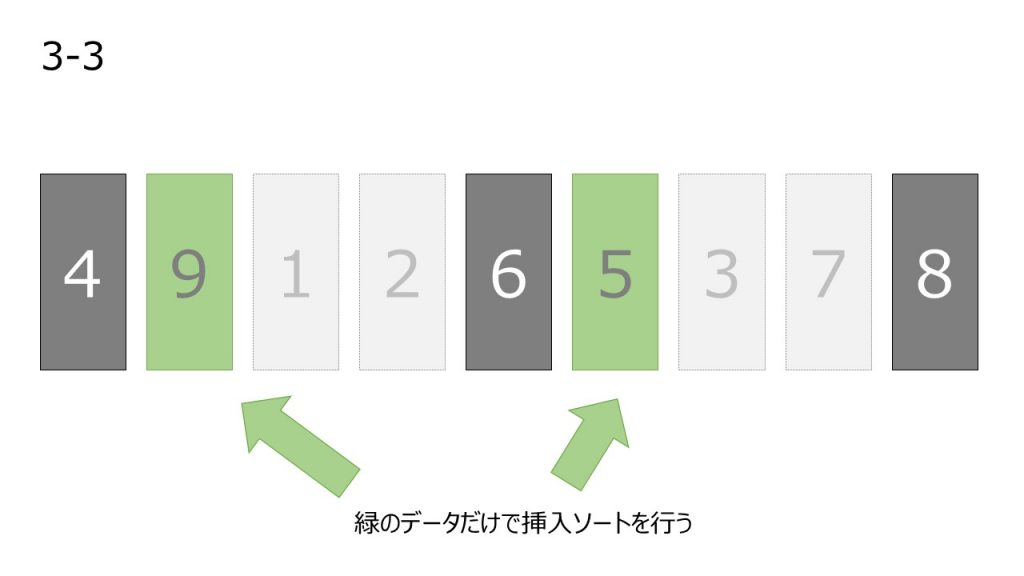
間隔 h を空けて取り出したデータ列に挿入ソートを適用する
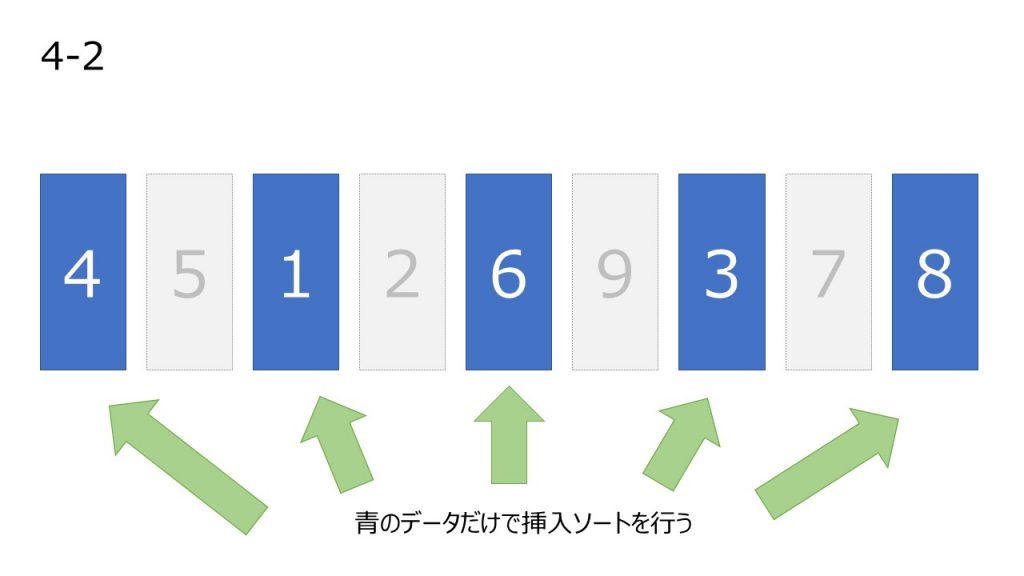
間隔 h を狭めて、2.を適用する操作を繰り返す。(今回は1すなわち普通の挿入ソートを適用する)
h=1 になったら、最後に挿入ソートを適用して終了

処理の上記処理

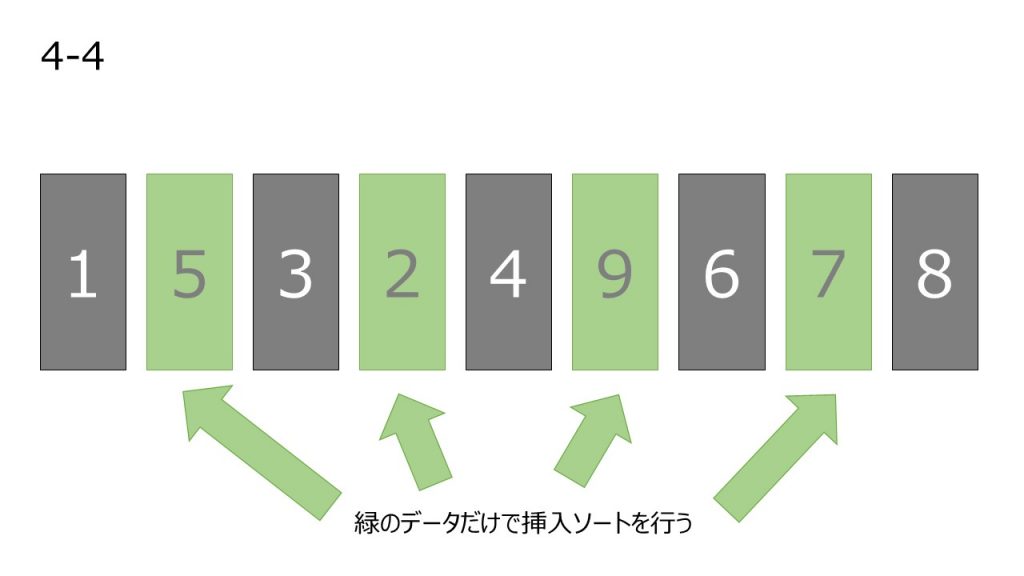
オーダー

オーダーは以下です。

最悪計算量 $O(n(logn)^2)$
最良計算量 $O(nlogn)$
平均計算量 $O(n^{1.25})$

平均計算量は $O(n^{1.25})$ と書きましたが、hのとり方によって計算量は異なります。
hの間隔が以下の場合 $O(n^{1.25})$ となるようです。
$1, 4, 13, … , (3^{k} - 1) / 2$
とされています。

参考：The Art of Computer Programming

コード

シェルソートのコードを考えてみました。
コードはC#で書いています。
hの間隔は $(3^{k} - 1) / 2$ になるように取っています。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();

      // 1～100の数字をバラバラに配列に入れる
      // いつもより多く100データをソートする
      for (var i = 1; i < 101; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

      Console.WriteLine("{" + string.Join(",", array) + "}");

      Console.WriteLine("{" + string.Join(",", ShellSort(array)) + "}");
    }

    public static int[] ShellSort(int[] arr)
    {
      // 間隔は 3^i - 1 / 2 となるように設定する
      // 1, 4, 13, 40,　...
      // そのため、要素数を考えて上記を満たす最大の指数を考える
      var index = (int)Math.Log(arr.Length, 3);
      var result = arr;


      for (var i = index; i > 0; i--)
      {
        // 間隔をあけてInsertSortを繰り返す
        var interval = (int)(Math.Pow(3, i) - 1) / 2;

        result = InsertSort(result, interval);
      }

      return result;
    }

    // InsertSortもintervalを開けられるよう改良
    public static int[] InsertSort(int[] arr, int interval)
    {
      // はじめのデータはソート済みとするため、interbal分はスキップしてスタート
      for (var i = interval; i < arr.Length; i++)
      {
        for (var sort = i; sort > 0; sort--)
        {

          // intarbal分前の数字と大小比較。左の数字のほうが小さければ抜ける
          if (sort % interval != i % interval)
          {
            continue;
          }

          var target = sort - interval;
          if (target < 0 || arr[sort] > arr[target])
          {
            break;
          }

          var tmp = arr[sort];
          arr[sort] = arr[target];
          arr[target] = tmp;
        }
      }

      return arr;
    }
  }
}

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～100の数字をバラバラに配列に入れる

// いつもより多く100データをソートする

for (var i = 1; i < 101; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", array) + "}");

Console.WriteLine("{" + string.Join(",", ShellSort(array)) + "}");

}

public static int[] ShellSort(int[] arr)

{

// 間隔は 3^i - 1 / 2 となるように設定する

// 1, 4, 13, 40,　...

// そのため、要素数を考えて上記を満たす最大の指数を考える

var index = (int)Math.Log(arr.Length, 3);

var result = arr;

for (var i = index; i > 0; i--)

{

// 間隔をあけてInsertSortを繰り返す

var interval = (int)(Math.Pow(3, i) - 1) / 2;

result = InsertSort(result, interval);

}

return result;

}

// InsertSortもintervalを開けられるよう改良

public static int[] InsertSort(int[] arr, int interval)

{

// はじめのデータはソート済みとするため、interbal分はスキップしてスタート

for (var i = interval; i < arr.Length; i++)

{

for (var sort = i; sort > 0; sort--)

{

// intarbal分前の数字と大小比較。左の数字のほうが小さければ抜ける

if (sort % interval != i % interval)

{

continue;

}

var target = sort - interval;

if (target < 0 || arr[sort] > arr[target])

{

break;

}

var tmp = arr[sort];

arr[sort] = arr[target];

arr[target] = tmp;

}

return arr;

}

マージソート

概要

マージソートはソートしたい数列を同じ長さの2つの数列に分割していきます。
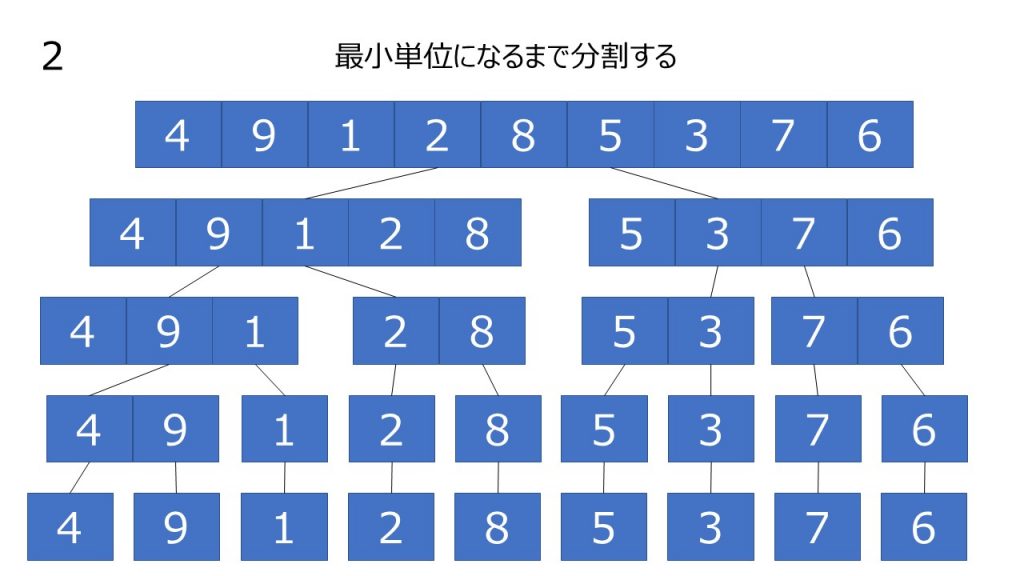
これ以上分割できない長さまで分割を繰り返し(つまりは1つの数字になるまで)ます。
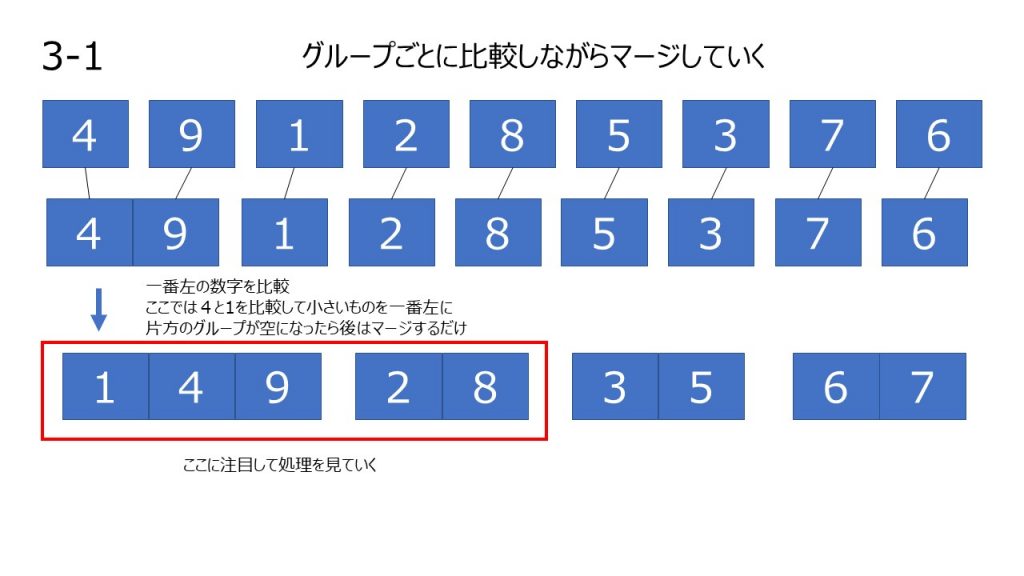
その後、隣のグループとソートしながら統合していきます。
これをすべてが統合されるまで繰り返します。

2つのグループを1つずつマージしていき最終的に統合した時ソートが完了していることからマージソートと呼ばれます。

処理

元データを用意する
数列を半分に分割していき最小単位に分割されるまで分割を繰り返す(最小単位とは、要素数1の数列)
隣り合うグループを統合する。その際、各グループの一番左の数字同士を比較して、左に小さい数字が配置されるように統合していく
4をグループが1つになるまで繰り返す

処理の上記処理

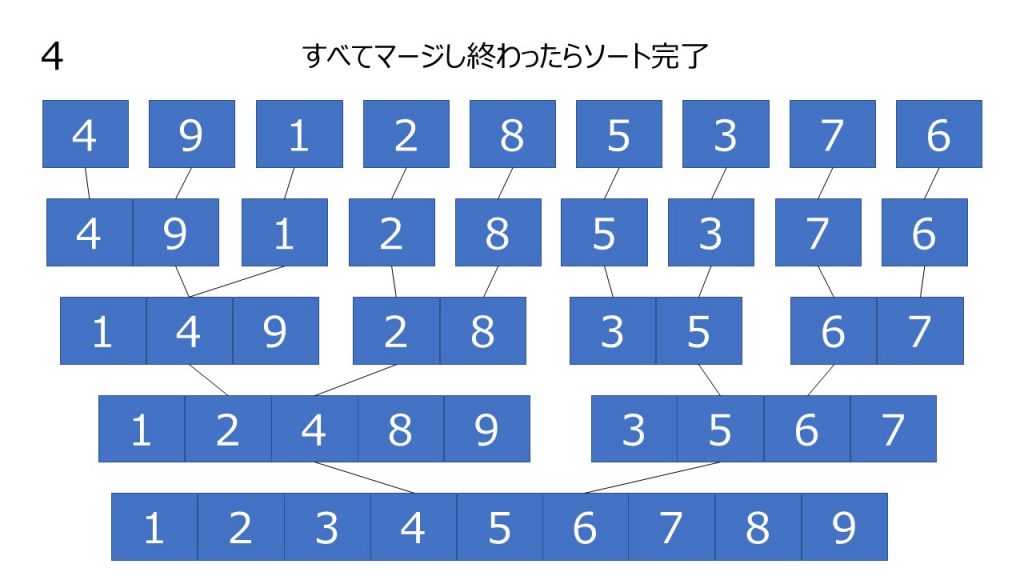
オーダー

オーダーは以下です。

最悪計算量 $O(nlogn)$
最良計算量 $O(nlogn)$
平均計算量 $O(nlogn)$

分割していくと $logn$ 段処理をすることが分かります。
要素 $n$ の半分、半分、半分、と $logn$ 回半分にすると要素が1となります。
少し分かりづらいですが、数列にすると、

$n / 2 / 2 / 2 \cdot\cdot\cdot\cdot = 1$

としたいので、 $/2$ が $m$ 回登場したと考えると、式変形すると

$(n / 2)^m = 1$
$n = 2^m$
$logn = m$ (両辺 $log_2$ で対数を取りました。アルゴリズムの世界では $log$ が出てくる時は底の2を省略します)

となるため、 $logn$ 回割りましたということになります。
1段あたりの処理のオーダーは $O(n)$ となりますので、計算量は $O(n) \times O(logn)$ となり、 $O(nlogn)$ となります

コード

マージソートのコードを考えてみました。
コードはC#で書いています。
グループごとに一番左の数字が小さいという性質を利用して、Queueを用いて実装してみました。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();

      // 1～100の数字をバラバラに配列に入れる
      for (var i = 1; i < 101; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

      Console.WriteLine("{" + string.Join(",", array) + "}");

      Console.WriteLine("{" + string.Join(",", MergeSort(array)) + "}");
    }

    private static Queue<int> tmp = new Queue<int>();

    public static int[] MergeSort(int[] arr)
    {
      // 0 から 最後の番号まで処理する
      Recursive(arr, 0, arr.Count() - 1);
      return arr;
    }

    private static void Recursive(int[] arr, int left, int right)
    {
      if (left < right)
      {
        var mid = (left + right) / 2;

        // 左のグループを再帰的に分割
        Recursive(arr, left, mid);

        // 右のグループを再帰的に分割
        Recursive(arr, mid + 1, right);

        Merge(arr, left, mid, right);
      }
    }

    private static void Merge(int[] arr, int left, int mid, int right)
    {
      tmp.Clear();

      // 左のグループをキューに詰める
      var leftItems = new Queue<int>(arr.ToList().GetRange(left, mid - left + 1));

      // 右のグループにキューを詰める
      var rightItems = new Queue<int>(arr.ToList().GetRange(mid + 1, right - mid));

      // 各グループの一番左の要素を比べて小さい方を採用していく
      while (leftItems.Count != 0 && rightItems.Count != 0)
      {
        if (leftItems.Peek() < rightItems.Peek())
        {
          tmp.Enqueue(leftItems.Dequeue());
          continue;
        }

        tmp.Enqueue(rightItems.Dequeue());
      }

      // あまった方をまるごと詰める
      var list = tmp.ToList();
      var addItems = leftItems.Count != 0
        ? leftItems
        : rightItems;

      list.AddRange(addItems);

      tmp = new Queue<int>(list);

      // Queueに詰めた分だけループが回る
      for (var i = left; i <= right; i++)
      {
        arr[i] = tmp.Dequeue();
      }
    }
  }
}

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～100の数字をバラバラに配列に入れる

for (var i = 1; i < 101; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", array) + "}");

Console.WriteLine("{" + string.Join(",", MergeSort(array)) + "}");

}

private static Queue<int> tmp = new Queue<int>();

public static int[] MergeSort(int[] arr)

{

// 0 から最後の番号まで処理する

Recursive(arr, 0, arr.Count() - 1);

return arr;

}

private static void Recursive(int[] arr, int left, int right)

{

if (left < right)

{

var mid = (left + right) / 2;

// 左のグループを再帰的に分割

Recursive(arr, left, mid);

// 右のグループを再帰的に分割

Recursive(arr, mid + 1, right);

Merge(arr, left, mid, right);

}

private static void Merge(int[] arr, int left, int mid, int right)

{

tmp.Clear();

// 左のグループをキューに詰める

var leftItems = new Queue<int>(arr.ToList().GetRange(left, mid - left + 1));

// 右のグループにキューを詰める

var rightItems = new Queue<int>(arr.ToList().GetRange(mid + 1, right - mid));

// 各グループの一番左の要素を比べて小さい方を採用していく

while (leftItems.Count != 0 && rightItems.Count != 0)

{

if (leftItems.Peek() < rightItems.Peek())

{

tmp.Enqueue(leftItems.Dequeue());

continue;

}

tmp.Enqueue(rightItems.Dequeue());

}

// あまった方をまるごと詰める

var list = tmp.ToList();

var addItems = leftItems.Count != 0

? leftItems

: rightItems;

list.AddRange(addItems);

tmp = new Queue<int>(list);

// Queueに詰めた分だけループが回る

for (var i = left; i <= right; i++)

{

arr[i] = tmp.Dequeue();

}

クイックソート

概要

クイックソートでは基準となる数(ピボットと呼びます。)を数列の中からランダムに1つ選びます。
そしてピボット以外の数をピボットより小さい数、大きい数の2グループに分けていきます。
その後、それぞれのグループでまたピボットを選定してそれぞれ小さい数大きい数にどんどん振り分けていく作業を繰り返すことで全体をソートします。
C#のSortメソッドはクイックソートを実装しています。
名前の通り、一番早いソートと言われていますが、並びが悪いと $O(n^2)$ の計算量がかかってしまうことが特徴です。
クイックソートとは名前が潔くてかっこいいですね。自負を感じますね。

処理

元データを用意する
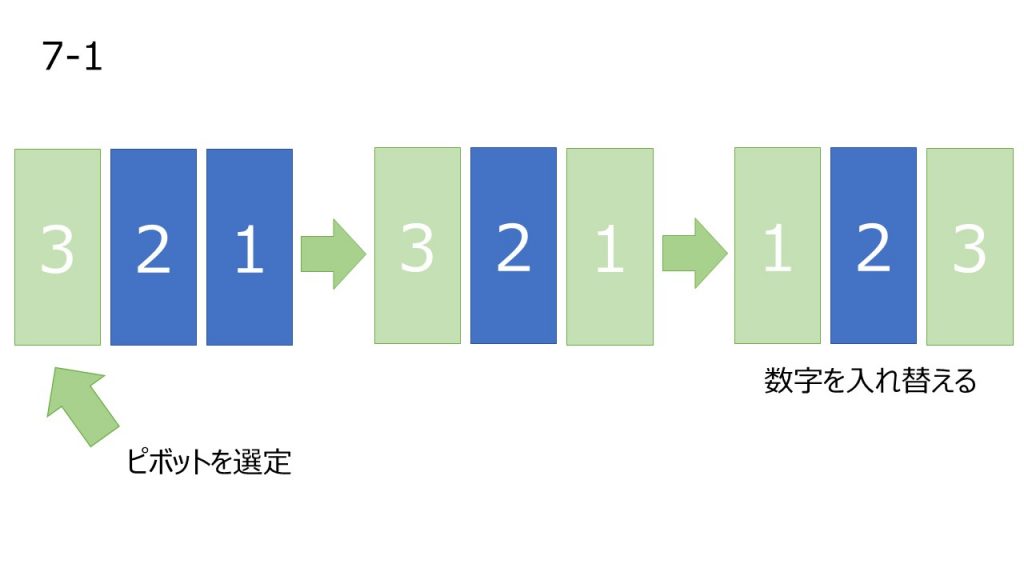
基準となるピボットを数列グループの中から選ぶ
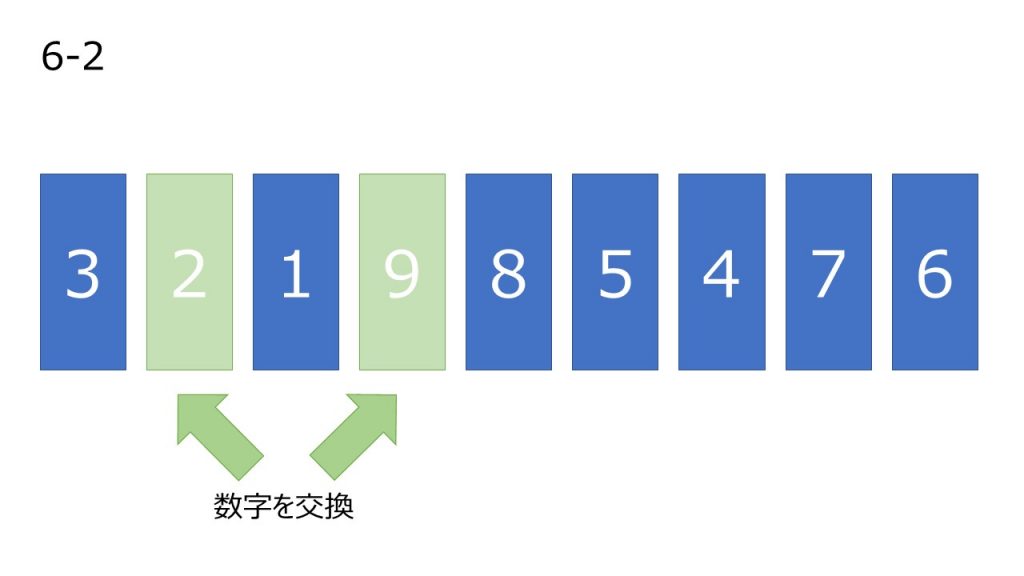
数列グループの中の一番左から走査し、基準のピボット以上の数字を選び、インデックスを記憶。
数列グループの中の一番右から走査し、基準のピボットより小さい数字を選び、インデックスを記憶。
3, 4 で記憶したインデックスの数値を入れ替える。
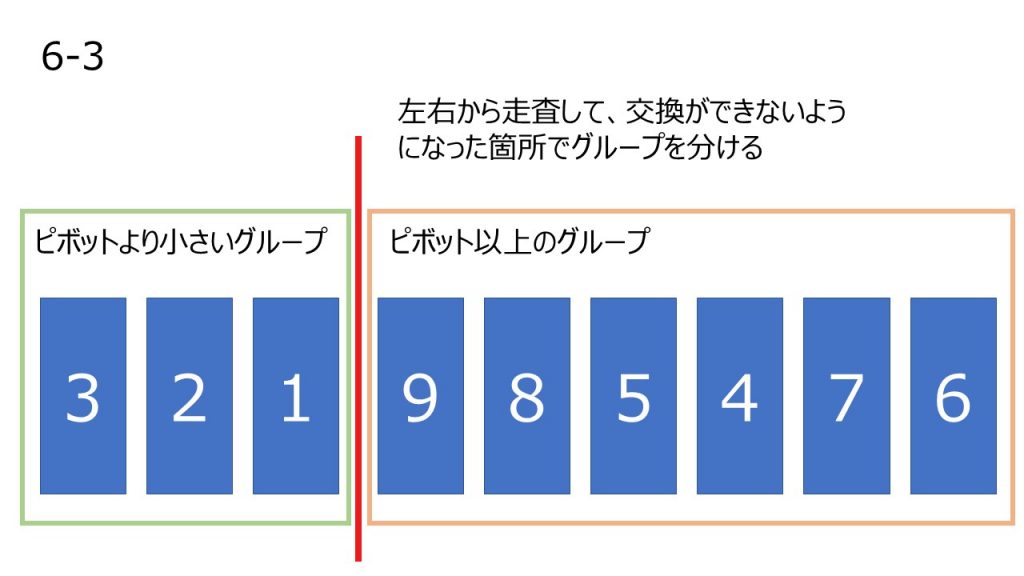
3~5の操作を繰り返し、3で走査しているインデックスが4で走査しているインデックスを超えた数字を記憶(すべてを走査しきった状態になる)。
この処理で得た数字はピボットの数より小さいグループと大きいグループに区分けしたこととなる。
小さいグループと大きいグループでそれぞれ3~6の操作を繰り返す。

処理の上記処理

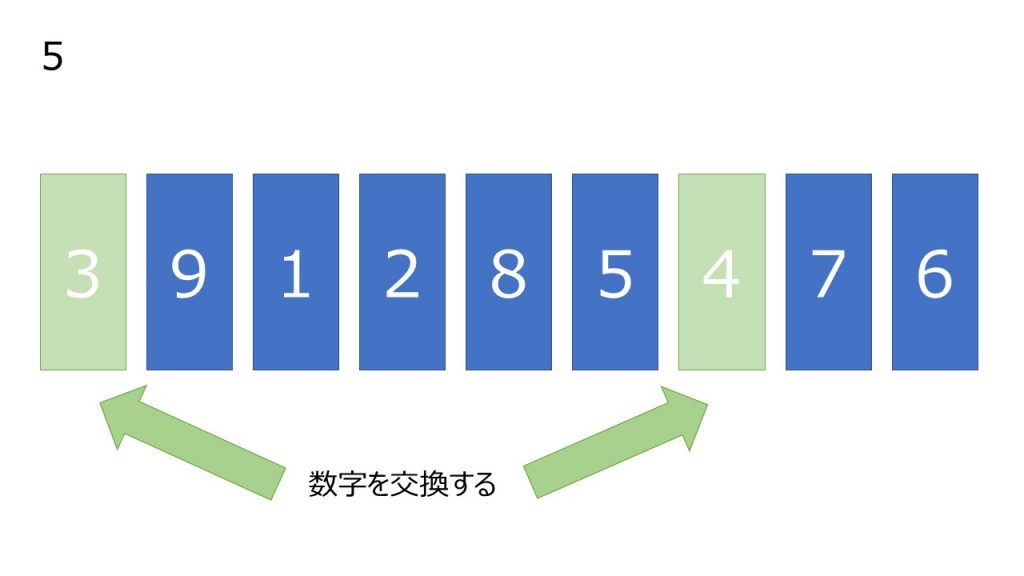
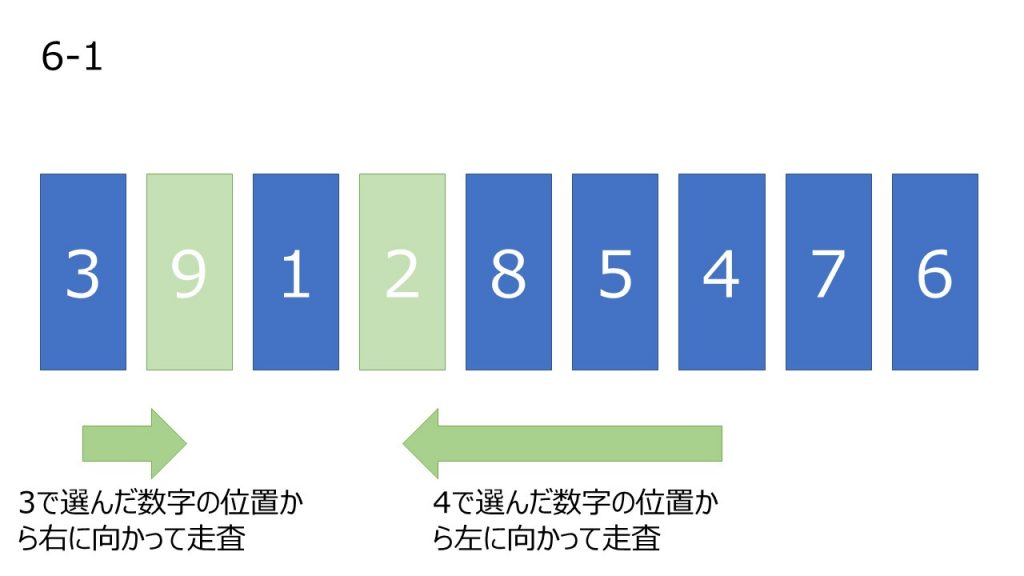
オーダー

最悪計算量 $O(n^2)$
最良計算量 $O(nlogn)$
平均計算量 $O(nlogn)$

基本的に2分割していくことになるので、平均はマージソートと同等の $O(nlogn)$ となります。
最悪の計算時間は逆順ソートになった場合再帰処理が $n$ 段になってしまうため、 $O(n^2)$ となってしまう。

ピボット軸の選定

クイックソートは少し特殊でピボットの選定が重要です。
というのも、できるだけ半分に分割できた方が処理の時間が短くなります。
そのためできるだけ中央値を選出したいのですが、選定に時間をかけるのも本末転倒です。
選定方式は以下のような候補があります。

案1. 左端の要素
案2. ランダムに選んだ位置の要素
案3. 左端，中央，右端の要素の中央値の要素
案4. 左から見て最初に得られた2つの異なる値の大きい方の要素(3,3,5,4,6,2 みたいな感じだと、3,5を選出する)

案1～3の場合は、最小値を選択してしまう可能性があります。
今回は案4で考えようと思います。

コード

クイックソートのコードを考えてみました。
コードはC#で書いています。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();

      // 1～100の数字をバラバラに配列に入れる
      for (var i = 1; i < 101; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

      Console.WriteLine("{" + string.Join(",", array) + "}");

      Console.WriteLine("{" + string.Join(",", QuickSort(array)) + "}");
    }

    public static int[] QuickSort(int[] arr)
    {
      GroupSort(arr, 0, arr.Length - 1);
      return arr;
    }

    private static void GroupSort(int[] arr, int left, int right)
    {
      // 左から確認していくインデックスを格納。
      var l = left;

      // 右から確認していくインデックスを格納。
      var r = right;


      // 要素数が1以下の領域ができた場合、その領域は確定とする。
      if (r - l < 1)
      {
        return;
      }

      var pivot = GetPivot(arr, l, r);


      while (true)
      {
        // ピボットの値以上の値を持つ要素を左から確認。
        while (arr[l] < pivot)
        {
          l++;
        }

        // ピボットの値より小さい値を持つ要素を右から確認。
        while (arr[r] >= pivot)
        {
          r--;
        }

        // 左から確認したインデックスが、右から確認したインデックス以上であれば外側のwhileループを抜ける。
        if (l > r)
        {
          break;
        }

        // そうでなければ、見つけた要素を交換。
        int temp = arr[r];
        arr[r] = arr[l];
        arr[l] = temp;

        // 交換を行なった要素の次の要素にインデックスを進める。
        l++;
        r--;
      }
      // 左側の範囲について再帰的にソートを行なう。
      GroupSort(arr, left, l - 1);

      // 右側の範囲について再帰的にソートを行なう。
      GroupSort(arr, r + 1, right);
    }

    private static int GetPivot(int[] arr, int left, int right)
    {

      // 要素が1以下になることはないがケアする
      if (left == right)
      {
        throw new Exception();
      }

      var result = int.MinValue;
      var count = 0;

      for (var i = left; i <= right; i++)
      {
        if (count > 1)
        {
          break;
        }

        if (result < arr[i])
        {
          result = arr[i];
          count++;
        }
      }

      return result;
    }
  }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～100の数字をバラバラに配列に入れる

for (var i = 1; i < 101; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", array) + "}");

Console.WriteLine("{" + string.Join(",", QuickSort(array)) + "}");

}

public static int[] QuickSort(int[] arr)

{

GroupSort(arr, 0, arr.Length - 1);

return arr;

}

private static void GroupSort(int[] arr, int left, int right)

{

// 左から確認していくインデックスを格納。

var l = left;

// 右から確認していくインデックスを格納。

var r = right;

// 要素数が1以下の領域ができた場合、その領域は確定とする。

if (r - l < 1)

{

return;

}

var pivot = GetPivot(arr, l, r);

while (true)

{

// ピボットの値以上の値を持つ要素を左から確認。

while (arr[l] < pivot)

{

l++;

}

// ピボットの値より小さい値を持つ要素を右から確認。

while (arr[r] >= pivot)

{

r--;

}

// 左から確認したインデックスが、右から確認したインデックス以上であれば外側のwhileループを抜ける。

if (l > r)

{

break;

}

// そうでなければ、見つけた要素を交換。

int temp = arr[r];

arr[r] = arr[l];

arr[l] = temp;

// 交換を行なった要素の次の要素にインデックスを進める。

l++;

r--;

}

// 左側の範囲について再帰的にソートを行なう。

GroupSort(arr, left, l - 1);

// 右側の範囲について再帰的にソートを行なう。

GroupSort(arr, r + 1, right);

}

private static int GetPivot(int[] arr, int left, int right)

{

// 要素が1以下になることはないがケアする

if (left == right)

{

throw new Exception();

}

var result = int.MinValue;

var count = 0;

for (var i = left; i <= right; i++)

{

if (count > 1)

{

break;

}

if (result < arr[i])

{

result = arr[i];

count++;

}

return result;

}

おわりに

今回は3つほどソートに関するアルゴリズムを考えていきました。
先人たちはいろいろな方法で効率の良いアルゴリズムを考えており、ソートだけでも随分な量になります。
各言語でソートのメソッドは用意されており、裏側を考えることは滅多にありませんが、こうやって改めてアルゴリズムを考えてみるのも勉強になって良いです。
よろしければ次回も見ていただけますと幸いです！

シリーズのブログの数も増えてきましたので、リンクを貼っておきます。

第0回 (初歩的な数学のアルゴリズムを考えてみよう)
第1回
 第2回
 第3回

アジャイル開発における計画

くじ引きとネイピア数

毎月アルゴリズム – 第4回 –

はじめに

アルゴリズムを考えてみる

シェルソート

概要

処理

処理の上記処理

オーダー

コード

マージソート

概要

処理

処理の上記処理

オーダー

コード

クイックソート

概要

処理

処理の上記処理

オーダー

ピボット軸の選定

コード

おわりに

最近の記事

顔認証（DeepFace vs GPT4o）

時系列解析再訪

πの新しい公式

中心極限定理

DBSCANを用いたクラスタリング

レイアウト解析

毎月アルゴリズム – 第6回 –

毎月アルゴリズム – 第2回 –

毎月アルゴリズム – 第7回 –

【モンテカルロ法】プログラミングで円周率を求める方法

【モンテカルロ法】ビュフォンの針の問題

毎月アルゴリズム – 第5回 –

Google Vision APIでOCR

アーカイブ

カテゴリー