毎月アルゴリズム – 第2回 –

はじめに

こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第2回目です。
いずれはアルゴリズムばかり載せていくことになると思いますが、初めのほうはアルゴリズムを考えるための前提を整理していけたら良いなと思います。
それでは早速考えていきましょう。

今回もアルゴリズムを考える前に

データ構造を考えようその1

下準備としてデータ構造の話をします。
コンピューターではデータはメモリに蓄えられていくことは皆さんご存じだと思います。
データをメモリに蓄える際に、データの順番や位置関係を規定したものをデータ構造と言います。
メモリに対するデータの格納の仕方は多くあり、それぞれ名前がついています。
適切なデータ構造を用いれば適切なアルゴリズムになったり、データ取得、入れ替え等の効率が良くなったりします。
今回は配列、リスト、ハッシュテーブルに関して解説します。
データ構造は文章での説明より図の説明のほうがわかりやすいので、少し図が多くなってしまいます。
退屈かもしれませんが見ていただけますと幸いです。

配列

配列はデータをメモリの連続した領域に格納するデータ構造です。
配列の名前をarrayとすると、その配列の一つ目のデータにはarray[0], 2つ目のデータにはarray[1]と順番を表す添え字を[]の中に表現します。
例えばデータをりんご、オレンジ、ぶどうを配列に格納すると、
array[0] → りんご
array[1] → オレンジ
array[2] → ぶどう
となります。

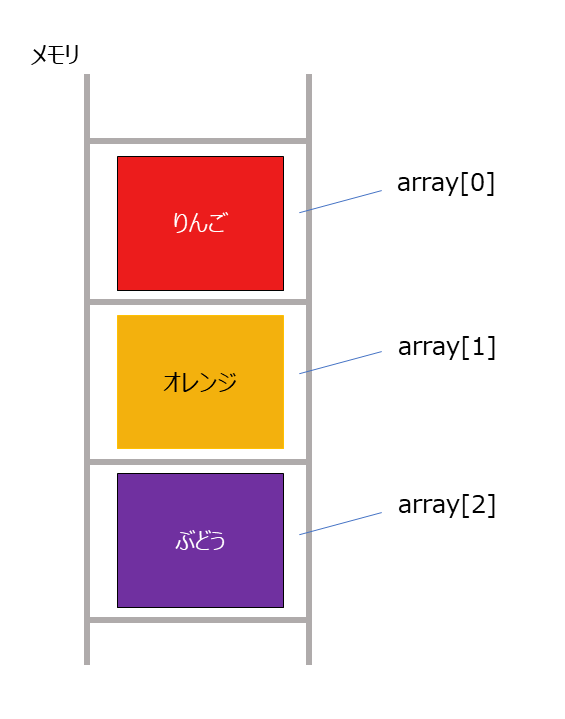
連続した領域に格納されているので、メモリアドレスには添え字を使って直接アクセスすることができます(これをランダムアクセスと言います)。
一方で、配列に対するデータの追加、削除のコストは少し高いです。
上記の配列の2番目にメロンを追加することを考えます。
その場合の手順は以下

配列の末尾に追加用の領域を確保
ぶどう → 空いている領域に移動
オレンジ → ぶどうのあった領域に移動
空いたオレンジの領域にメロンを追加

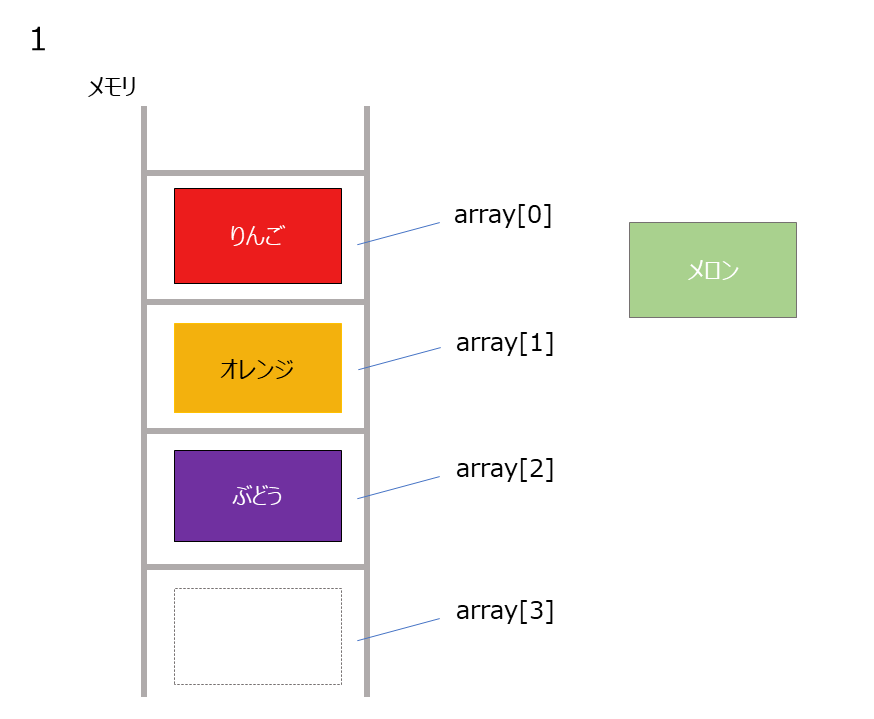
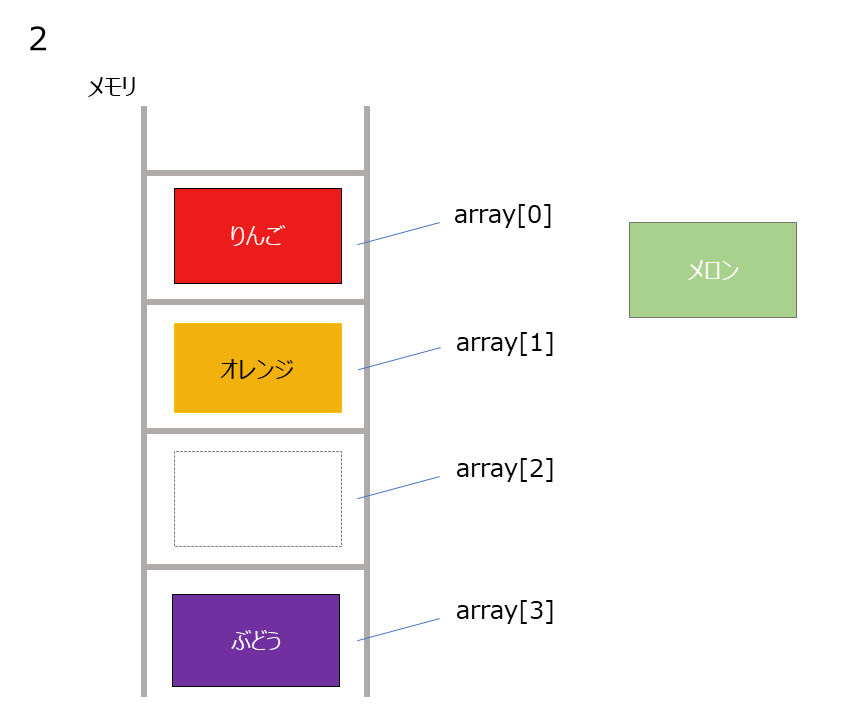
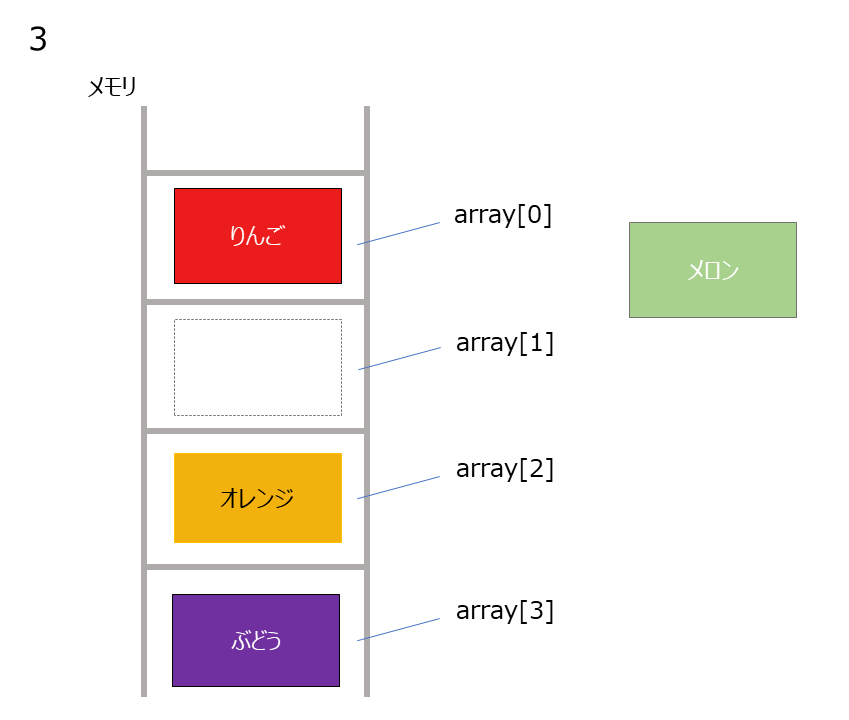
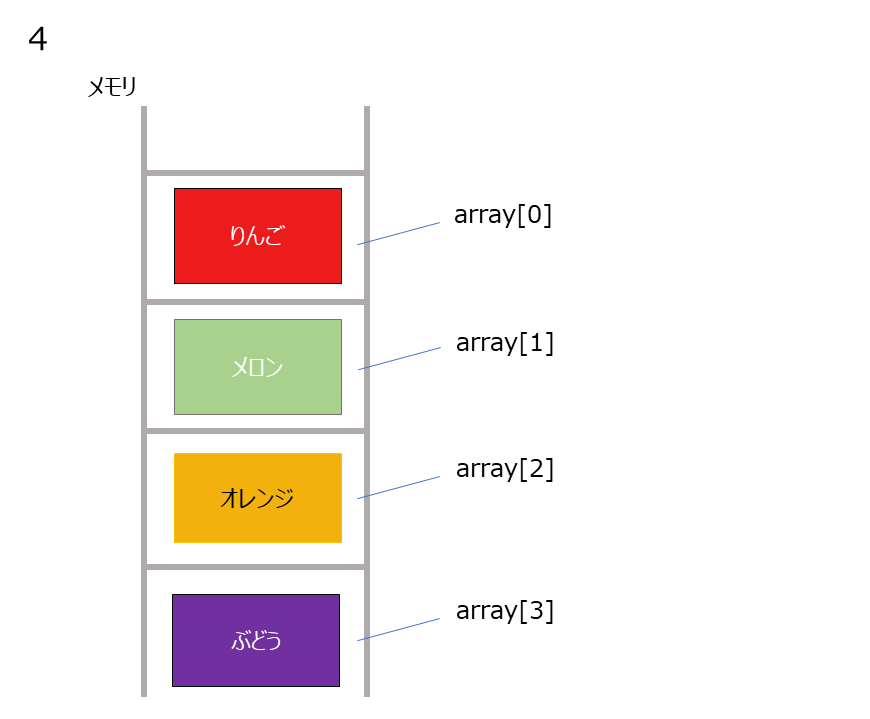
削除時は上記の図を逆の手順を踏んで削除していきます。

添え字を増やすことで、多次元の配列も実現できます。
以下は2次元配列の図です

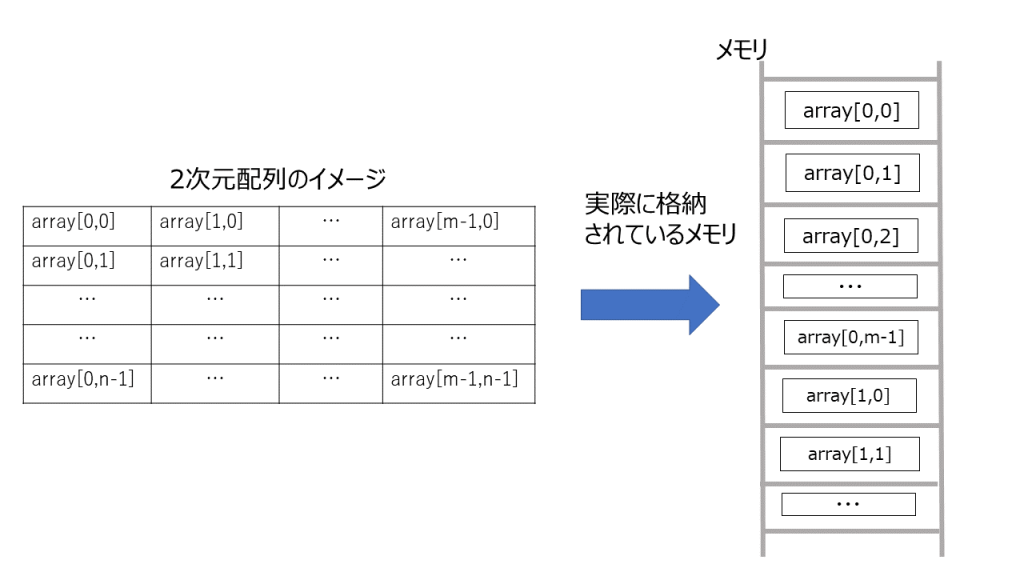
まとめ

配列は連続したメモリにデータを持つデータ構造
データへのアクセススピードは速い(オーダーは $O(1)$ )
配列に追加、削除するスピードは遅い(オーダーは $O(n)$ )

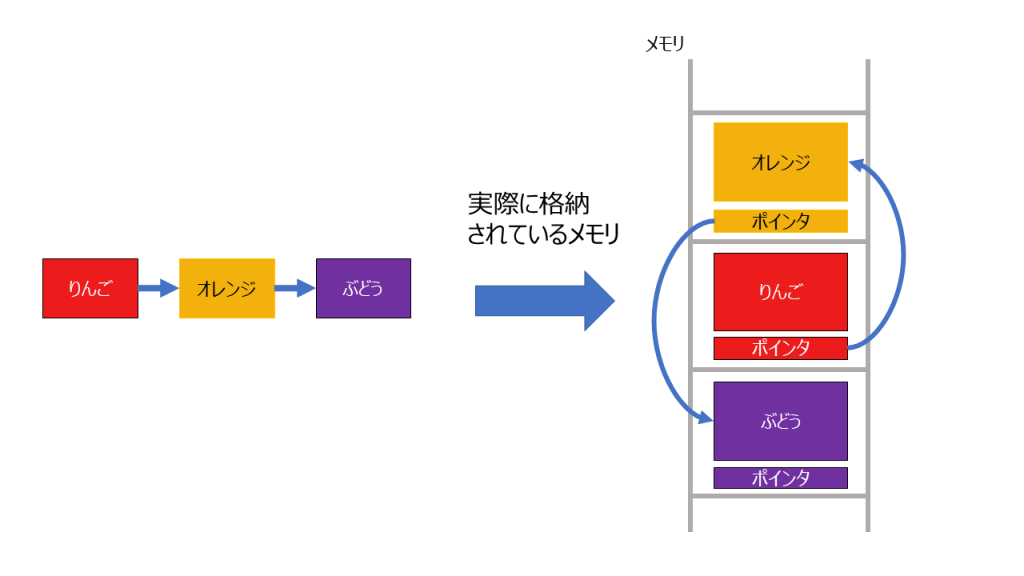
リストではデータがメモリ上に連続して格納されている必要はなく、バラバラに格納されています。
バラバラに格納されているので、各データにはポインタを頭からたどることしかできません(これをシーケンシャルアクセスと呼びます)。

データの追加は前後のポインタを差し替えるだけなので容易です。
りんごとぶどうの間にオレンジを追加したい場合を考えます

りんごのポインタをオレンジに差し替える
オレンジのポインタをぶどうに向ける

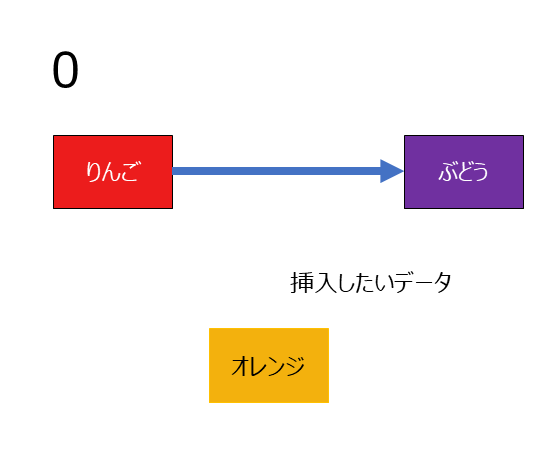
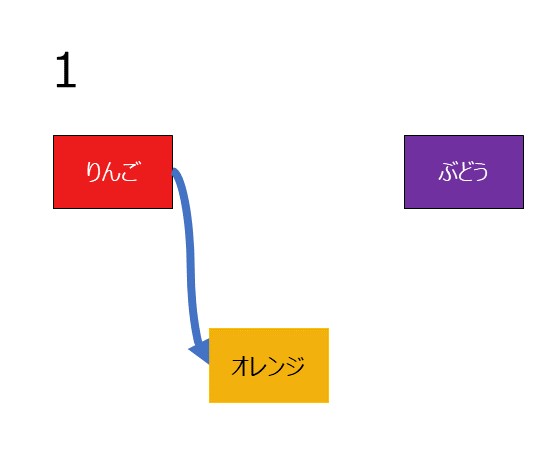
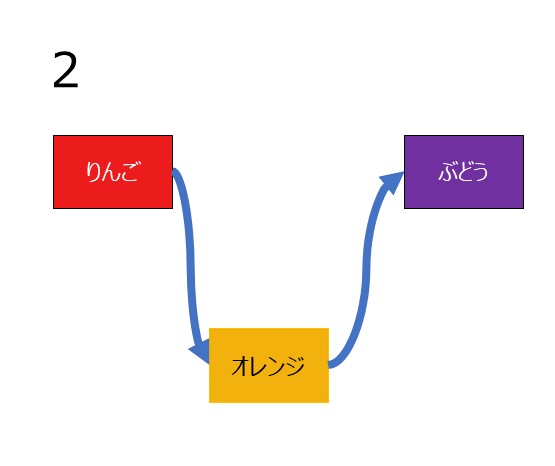
データの削除はもっと容易です。
上記のデータのオレンジを削除する場合

りんごのポインタをぶどうに差し替える

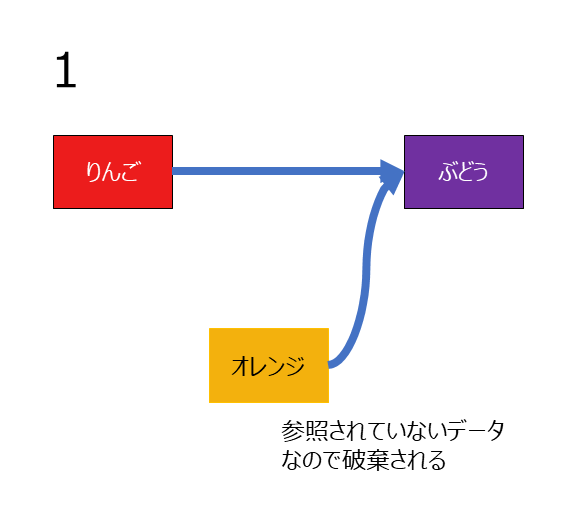
だけで十分です。
オレンジのポインタはぶどうに向いたままですが、どこからも参照されていないのでGCされるタイミングで再利用可能なメモリになるだけです。

まとめ

リストはデータとポインタが対になったデータ構造
ポインタは次のデータのアドレス情報を持っている
データへのアクセススピードは遅い(オーダーは $O(n)$ )
配列に追加、削除するスピードは速い(オーダーは $O(1)$ )

ハッシュテーブル

KeyとValueを一つのペアとしてデータを格納するデータ構造です。
連想配列や辞書という呼ばれ方をするケースもあります。

Keyからハッシュ値を求め、格納アドレスを決定し、ランダムアクセスが高速なのが特徴です。
同じKeyからは同じ数値が返ってくるメソッドのことをハッシュ関数と呼び、その関数から求められる値をハッシュ値と呼びます。

以下のようなKey-Valueのペアを考えましょう。

Key	Value
国語	80
数学	85
英語	77
社会	73
理科	89

C#におけるハッシュテーブル(Dictionary)の作成のされ方は以下になります。
少し難しい話になります。図示もするのでそちらを参照するほうが直感的に分かりやすいかもしれません。

buckets, entitesという配列を用意。配列の大きさは素数個入るものと考えれば良い。(なぜ素数個用意するかは割愛します。)
buckets: ハッシュコード->何個目のデータに次アクセスすべきかを格納しているものと考えれば良い
entites: 辞書データの一つ一つの要素と考えれば良い。
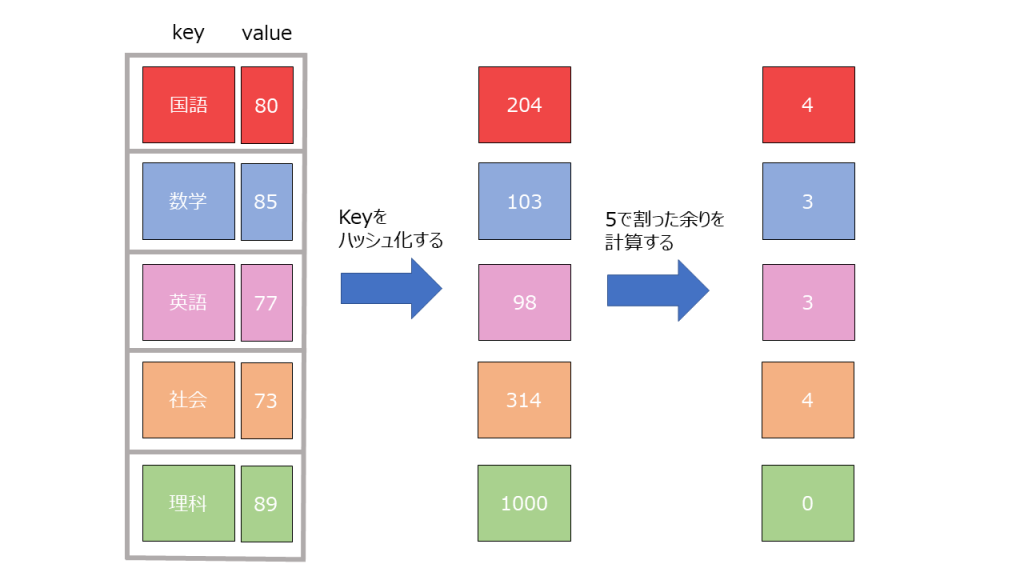
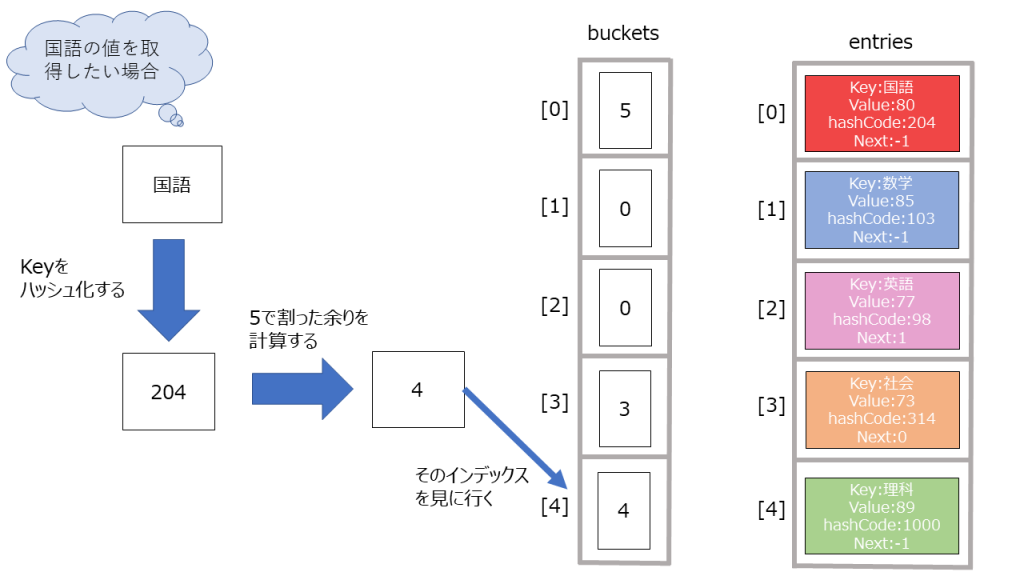
Keyをハッシュ関数にかけてハッシュ値を得る。

“国語” → 12345678
そのハッシュ値をbucketsの長さで割った余りを計算する。
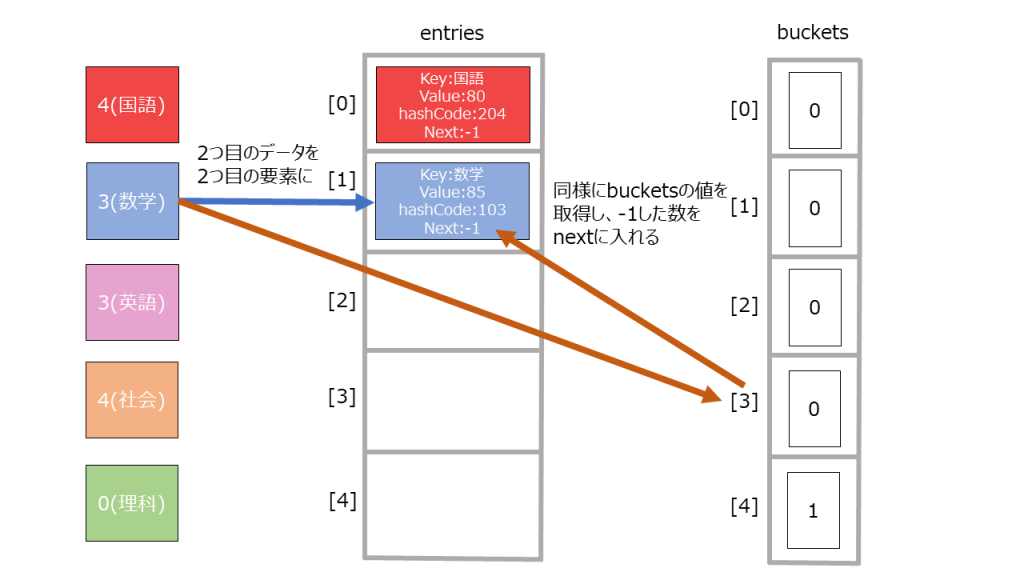
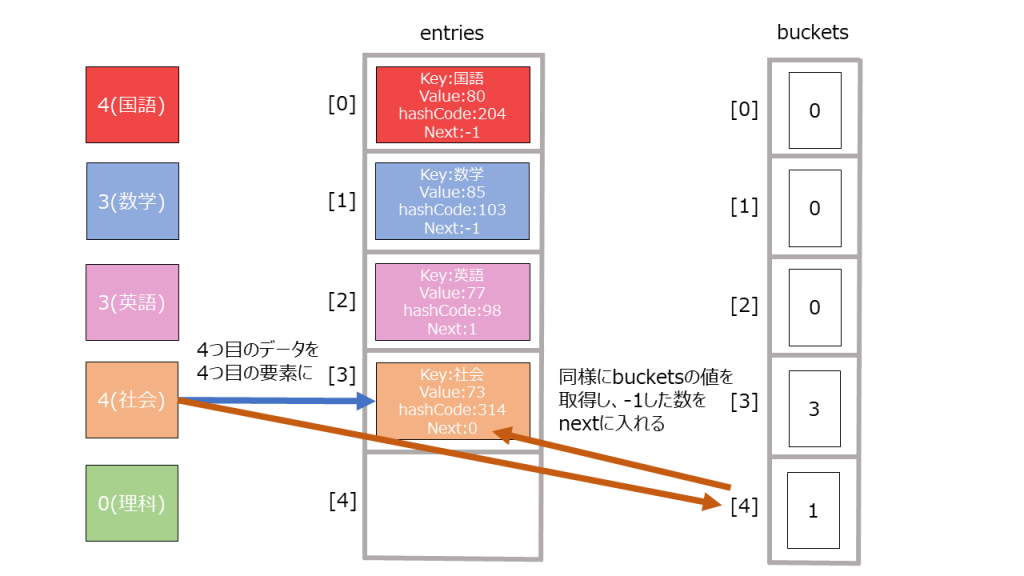
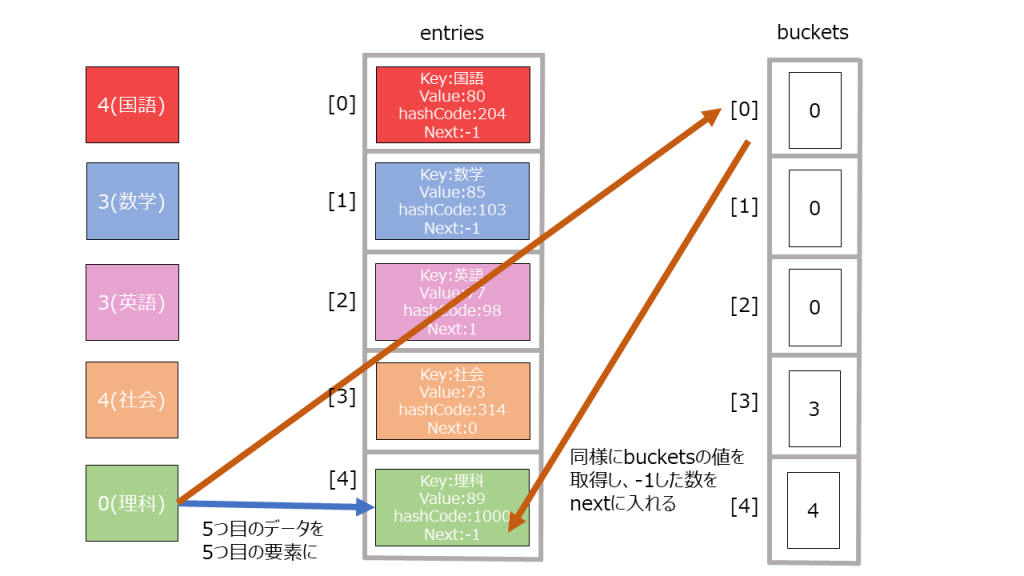
12345678 % bucket.Length = 2 ・・・(1)

entitesの末尾に新たにデータを作成する。その際、bucketsのインデックスが(1)の値のデータを取り出し、entityのnextの値とする(理由は後述)。

index = count // 今のデータ数
ref Entry entry = ref entries![index];
entry.hashCode = hashCode;
entry.next = bucket - 1;
entry.key = key;
entry.value = value;

index = count // 今のデータ数

ref Entry entry = ref entries![index];

entry.hashCode = hashCode;

entry.next = bucket - 1;

entry.key = key;

entry.value = value;

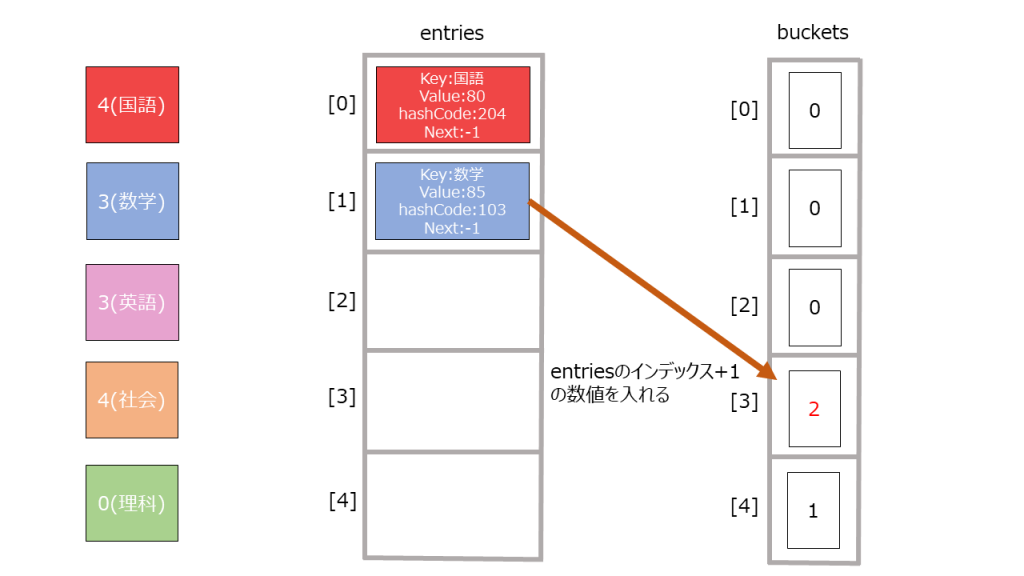
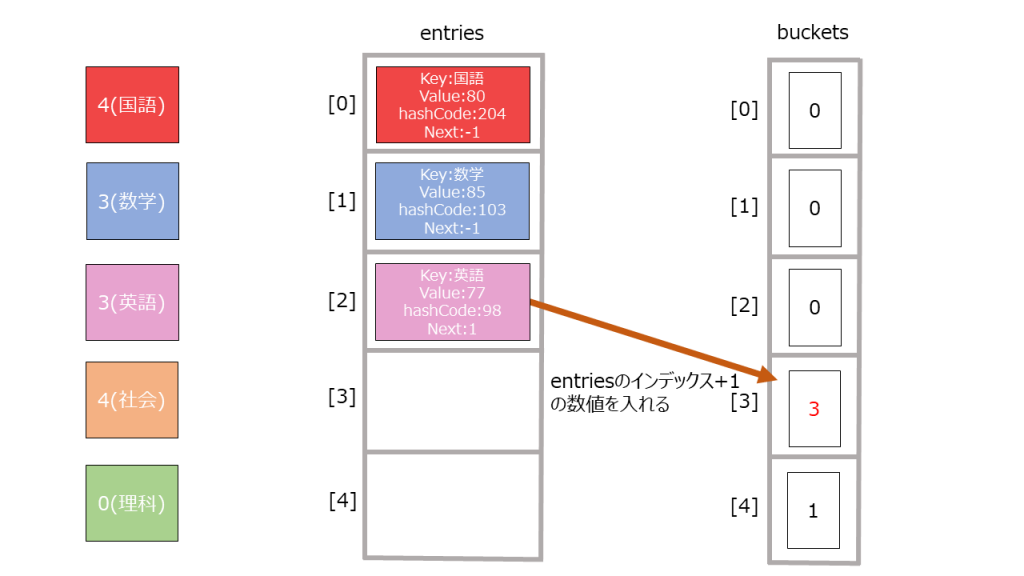
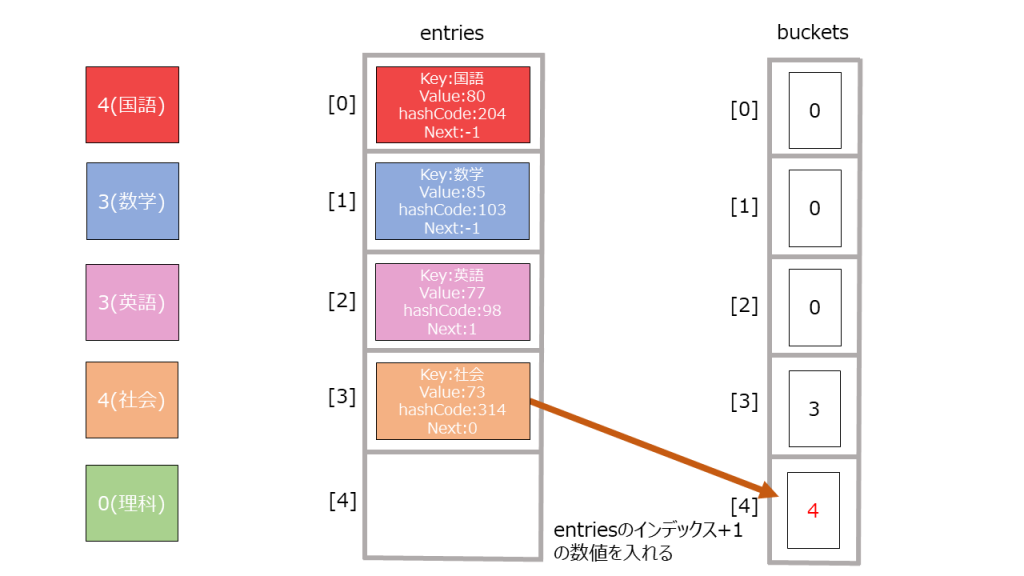
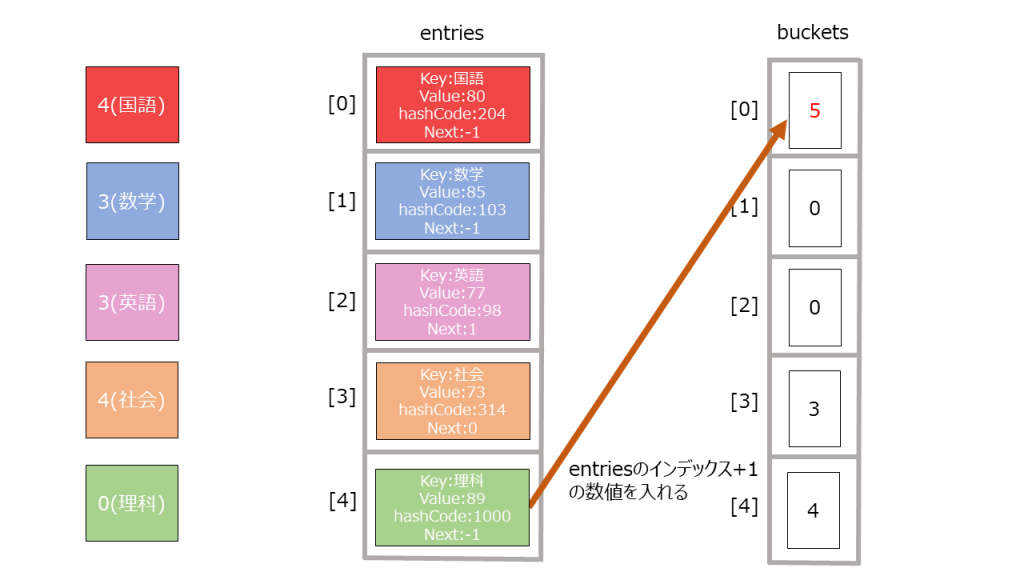
bucketsに未使用のインデックスを格納する。

C#

_buckets[2] = index + 1;

1

_buckets[2] = index + 1;

簡単に言うとこんな感じでハッシュ化し、そのハッシュ値を元に別の配列に置き直していく形になります。
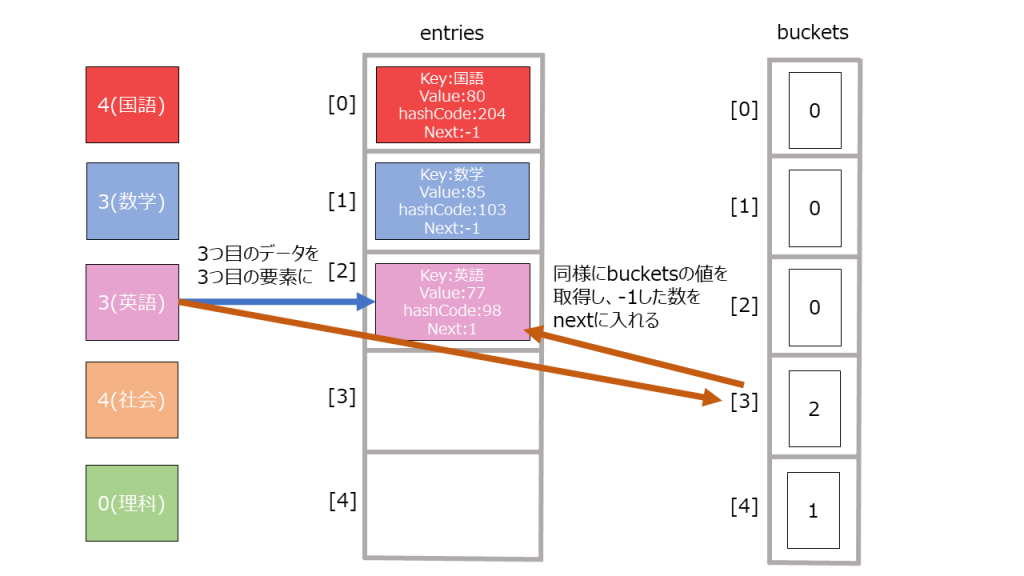
3でハッシュ値をbucketsの長さで割るとハッシュ値が異なっても同じ数値になってしまうことがあります(これをハッシュコードの衝突と言います)。
例えば以下のような感じです。

4 % 3 = 1
7 % 3 = 1

1 2	4 % 3 = 1 7 % 3 = 1

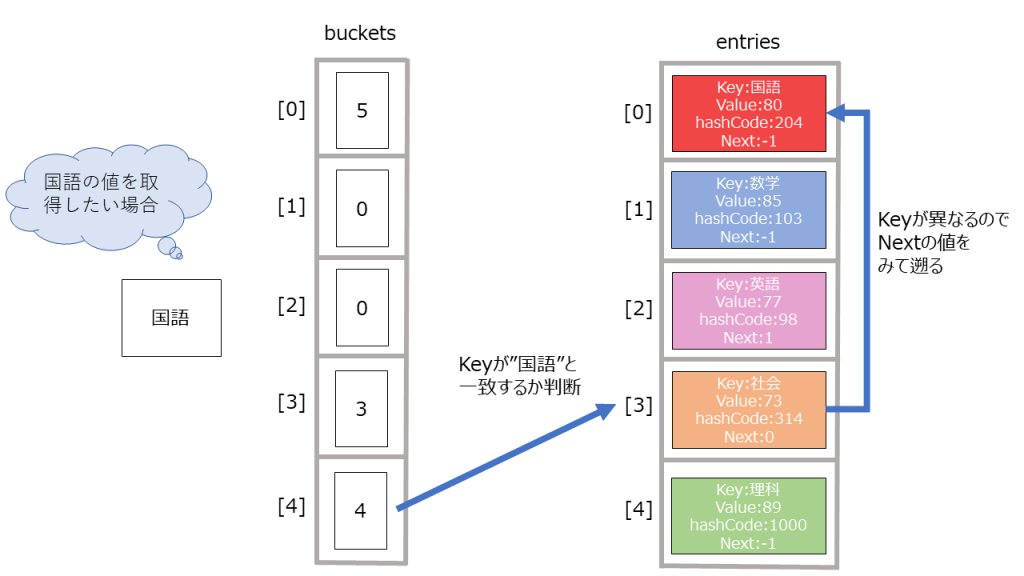
そういったときのために4の操作で同じ余りのときどのデータの次にどのデータが来るという情報を持っておく必要があります。

上記のようにkeyをハッシュコードに変換して、インデックスによるランダムアクセスをしているので、高速でデータを取得することができます(配列でやったようにランダムアクセスは高速でアクセスできるためです。)。

参考
https://source.dot.net/#System.Private.CoreLib/Dictionary.cs

データ登録時

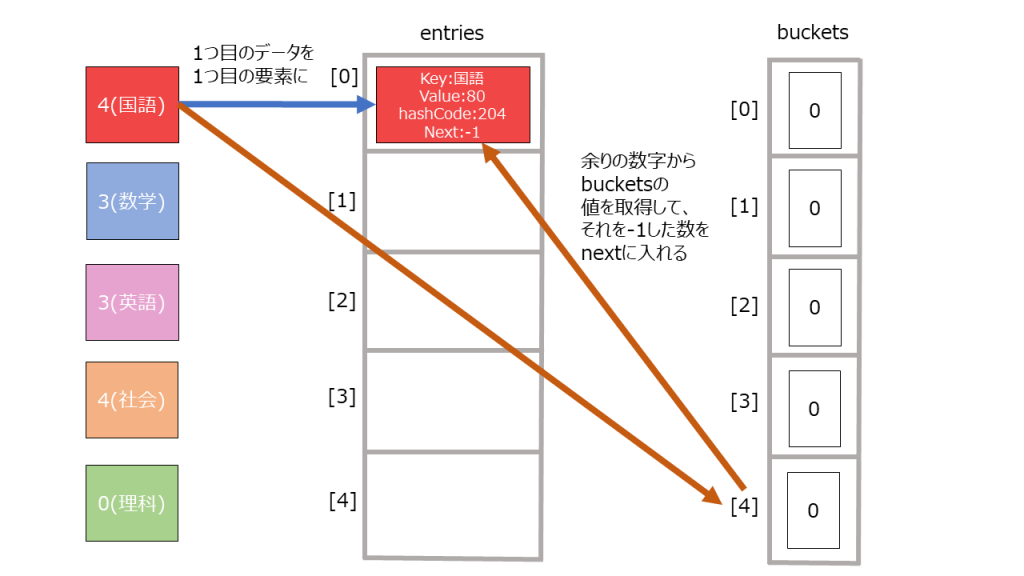
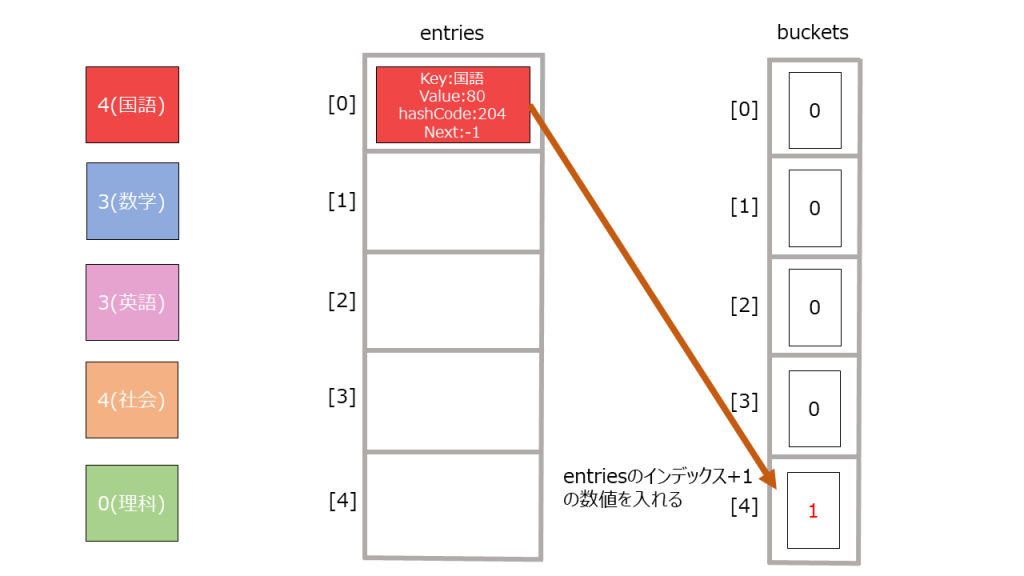
データ参照時

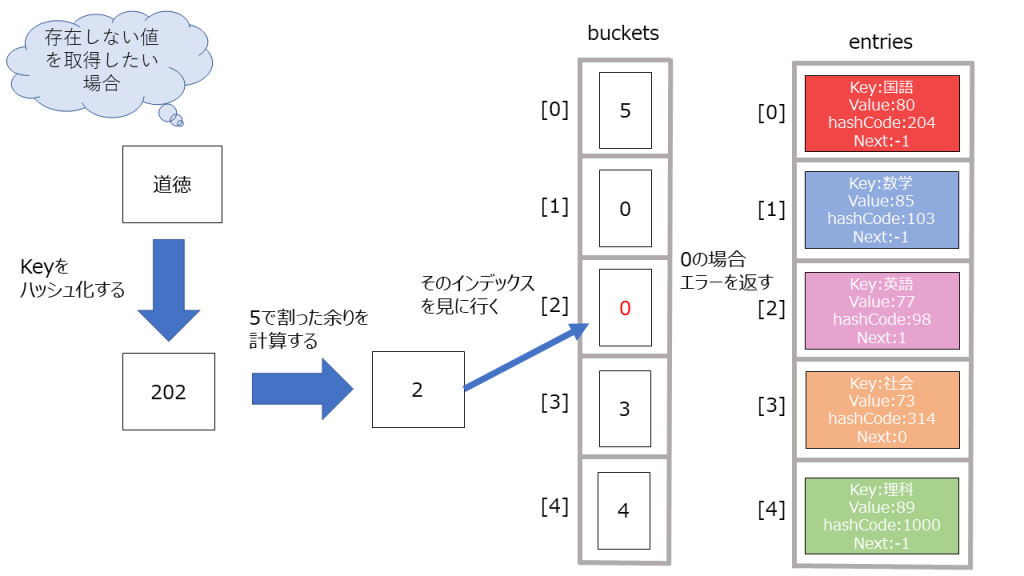
まとめ

ハッシュテーブルはKey-Valueのペアを持つデータ構造である
データへのアクセススピードは速い(オーダーは $O(1)$ )
データの追加も速い(オーダーは $O(1)$ )
使う場合はKey-Valueというペアを考えて利用するため、そのようなデータセットを処理したいときに用いる

データ構造に関するまとめ

データ構造はもう少し種類があるので残りは次回に回すとして、いくつかのデータ構造を見てきました。
用途に適したデータ構造を選択することで、アルゴリズムの処理速度に良い影響がでます。
例えば、前回の記事で用いたバブルソートですが、リストではなく配列を用意して処理を書きました。

private static int[] BubbleSort(int[] arr)
{
  for (var i = 0; i < arr.Length; i++)
  {
    // 右から隣り合わせになった数値を比較して入れ替える
    // ソート済みの数字には触れないようにする
    for (var sort = arr.Length - 1; sort > i; sort--)
    {
      if (arr[sort] < arr[sort - 1])
      {
        var tmp = arr[sort];
        arr[sort] = arr[sort - 1];
        arr[sort - 1] = tmp;
      }
    }
  }

  return arr;
}

private static int[] BubbleSort(int[] arr)

{

for (var i = 0; i < arr.Length; i++)

{

// 右から隣り合わせになった数値を比較して入れ替える

// ソート済みの数字には触れないようにする

for (var sort = arr.Length - 1; sort > i; sort--)

{

if (arr[sort] < arr[sort - 1])

{

var tmp = arr[sort];

arr[sort] = arr[sort - 1];

arr[sort - 1] = tmp;

}

return arr;

}

なんとなく配列を用いたわけではなく、意図して配列を用いて記載しました。
ソート等の処理は、データの追加、削除が存在しません。
そのため、 LinkedList<T> を用いると、追加削除には強いけどアクセススピードが遅いというのは今回のアルゴリズムにマッチしていないです。

このように用途に合わせてデータ構造を選択することで、高速性、安全性(変な操作ができない)を確保しながらアルゴリズムを記載することができます。

アルゴリズムを考えてみる

さて、前置きが長くなりましたが、本日もソートに関してアルゴリズムを考えていきます。
前回はバブルソートを考えてみましたが、今回は選択ソートです。

選択ソート

概要

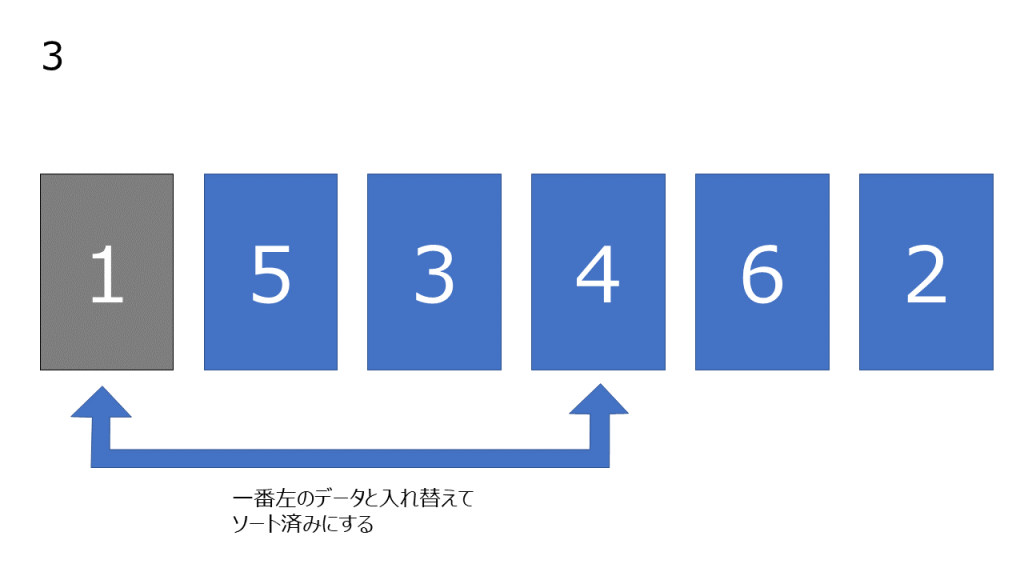
選択ソートはデータの中から最小の数値を検索し、左端の数字と入れ替える操作を繰り返してソートを行うアルゴリズムです。
データを線形探索して最小値を探します。

オーダー

オーダーは $O(n^2)$ です。
試行回数の計算は
$(n-1) + (n-2) + (n-3) + ...... + 3 + 2 + 1 = n(n-1) / 2$ 回となります。
バブルソートと同等の試行回数です。

処理

元データを用意する
データを線形探索して最小値を探す
そのデータと一番左のデータを交換し、一番左のデータをソート済みとする
ソート済みのデータを除いて残ったデータの一番最小のデータを線形探索する
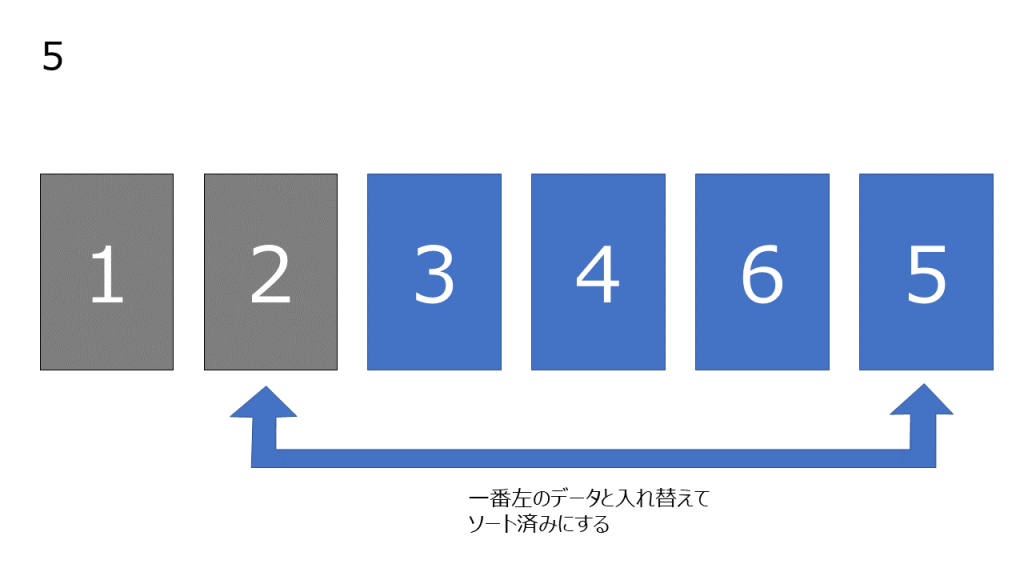
そのデータと残ったデータの一番左のデータを交換し、ソート済みとする
4 ~ 5 の操作を繰り返し、すべてがソート済みのデータになるまで行う

上記処理の簡易図

コード

前回と同じように選択ソートのコードを考えてみました。
コードはC#で書いています。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();
      
      // 1～20の数字をバラバラに配列に入れる
      for (var i = 1; i < 21; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

      Console.WriteLine("{" + string.Join(",", array) + "}");

      Console.WriteLine("{" + string.Join(",", SelectSort(array)) + "}");
    }

    public static int[] SelectSort(int[] arr)
    {
      for (var i = 0; i < arr.Length; i++)
      {
        var minIndex = i;

        // ソート済みの数字には触れないようにする
        for (var sort = arr.Length - 1; sort > i; sort--)
        {
          // 一番小さい数字のIndexをおさえる
          minIndex = arr[sort] < arr[minIndex]
            ? sort
            : minIndex;
        }

        // 一番左の数と同じの場合入れ替える必要がない
        if (i == minIndex)
        {
          continue;
        }

        var tmp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = tmp;
      }

      return arr;
    }
  }
}

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～20の数字をバラバラに配列に入れる

for (var i = 1; i < 21; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", array) + "}");

Console.WriteLine("{" + string.Join(",", SelectSort(array)) + "}");

}

public static int[] SelectSort(int[] arr)

{

for (var i = 0; i < arr.Length; i++)

{

var minIndex = i;

// ソート済みの数字には触れないようにする

for (var sort = arr.Length - 1; sort > i; sort--)

{

// 一番小さい数字のIndexをおさえる

minIndex = arr[sort] < arr[minIndex]

? sort

: minIndex;

}

// 一番左の数と同じの場合入れ替える必要がない

if (i == minIndex)

{

continue;

}

var tmp = arr[i];

arr[i] = arr[minIndex];

arr[minIndex] = tmp;

}

return arr;

}

終わりに

今回も前提となる知識とソートに関するアルゴリズムを考えていきました。
概要を図にまとめたので少し図の量が多くなってしまいましたが、より分かりやすくイメージを書いたつもりなので、
伝わればうれしい限りです。
ではまた第三回でお会いしましょう。

Salesforce Apexプログラミング／アノテーション

社員インタビュー第9弾：退職者にインタビューしてみた③

毎月アルゴリズム – 第2回 –

はじめに

今回もアルゴリズムを考える前に

データ構造を考えようその1

配列

まとめ

リスト

まとめ

ハッシュテーブル

データ登録時

データ参照時

まとめ

データ構造に関するまとめ

アルゴリズムを考えてみる

選択ソート

概要

オーダー

処理

上記処理の簡易図

コード

終わりに

最近の記事

顔認証（DeepFace vs GPT4o）

時系列解析再訪

πの新しい公式

中心極限定理

DBSCANを用いたクラスタリング

レイアウト解析

毎月アルゴリズム – 第7回 –

毎月アルゴリズム – 第1回 –

【モンテカルロ法】プログラミングで円周率を求める方法

毎月アルゴリズム – 第5回 –

初歩的な数学のアルゴリズムを考えてみよう

毎月アルゴリズム – 第3回 –

Google Vision APIでOCR

アーカイブ

カテゴリー

毎月アルゴリズム – 第2回 –

はじめに

今回もアルゴリズムを考える前に

データ構造を考えよう その1

配列

まとめ

リスト

まとめ

ハッシュテーブル

データ登録時

データ参照時

まとめ

データ構造に関するまとめ

アルゴリズムを考えてみる

選択ソート

概要

オーダー

処理

上記処理の簡易図

コード

終わりに

最近の記事

顔認証（DeepFace vs GPT4o）

時系列解析再訪

πの新しい公式

中心極限定理

DBSCANを用いたクラスタリング

レイアウト解析

毎月アルゴリズム – 第7回 –

毎月アルゴリズム – 第1回 –

【モンテカルロ法】プログラミングで円周率を求める方法

毎月アルゴリズム – 第5回 –

初歩的な数学のアルゴリズムを考えてみよう

毎月アルゴリズム – 第3回 –

Google Vision APIでOCR

アーカイブ

カテゴリー

データ構造を考えようその1