はじめに
こんにちは。よっしーです。
普段はアルゴリズムに関するブログをよく書いているのですが、今回はプログラムで確率計算を行う手法を紹介できればと思います。
数値計算を行うための手法の一つとして、モンテカルロシミュレーションを紹介したいと思います。
今回はそのシミュレーション手法をお伝えして、次回にはそのシミュレーションを用いて確率に円周率の ![]() が含まれるような面白い事象を紹介したいと思います。
が含まれるような面白い事象を紹介したいと思います。
モンテカルロシミュレーションとは
モンテカルロシミュレーションとは、一様な乱数を用いて数値計算を行いその近似値を得る手法のことを言います。
![]() 回の試行を行ってある事象が
回の試行を行ってある事象が ![]() 回起こった時、その事象が起こる確率は
回起こった時、その事象が起こる確率は ![]() で近似することができます。
で近似することができます。
試行回数が多ければ多いほど当然より良い近似になります。
実際にシミュレーションしてみる
例1: サイコロの出目の確率
サイコロの出目は 1~6 になります。
0~1 までの一様な乱数を作成することで 1~6 の出目を出せるサイコロを作成することが可能となり、そのサイコロを 3 つ振って出目の和が 12 となる確率を求めてみたいと思います。
理論値で計算すると、3 つサイコロを振って出目の和が 12 になる組み合わせは以下
● 3 つの出目が異なる組み合わせ
(1, 5, 6), (2, 4, 6), (3, 4, 5)
● 2 つの出目が異なる組み合わせ
(2, 5, 5), (3, 3, 6)
● すべての出目が同じ組み合わせ
(4, 4, 4)
順番を考える必要があり、順列組み合わせを考慮して確率は
![]()
上記をプログラムでシミュレーションするならコードは以下になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
using System; using System.Collections.Generic; using System.Linq; namespace ConsoleApp3 { class Program { static void Main(string[] args) { Console.WriteLine("TruthValue is : " + 25 / 216d); var numOfTrial = 101; Console.WriteLine("n = " + numOfTrial + ", 確率 : " + AllProbability(ThreeDiceRollChallange(numOfTrial))); numOfTrial = 10001; Console.WriteLine("n = " + numOfTrial + ", 確率 : " + AllProbability(ThreeDiceRollChallange(numOfTrial))); numOfTrial = 1000001; Console.WriteLine("n = " + numOfTrial + ", 確率 : " + AllProbability(ThreeDiceRollChallange(numOfTrial))); numOfTrial = 100000001; Console.WriteLine("n = " + numOfTrial + ", 確率 : " + AllProbability(ThreeDiceRollChallange(numOfTrial))); } private static readonly Random random = new(); // 1~6までの数字が一様に出力される private static int RollDice() { return (int)(random.NextDouble() * 6) + 1; } private static string AllProbability(IDictionary<int, int> dic) { var countAll = dic.Sum(x => x.Value); return string.Join(", ", dic.OrderBy(x => x.Key).Select(x => x.Key.ToString() + ": " + (x.Value / (double)countAll).ToString())); } private static IDictionary<int, int> ThreeDiceRollChallange(int numOfTrial) { return DiceRollChallange(numOfTrial, 3); } private static IDictionary<int, int> DiceRollChallange(int numOfTrial, int rollNum) { var dic = new Dictionary<int, int>(); for (var i = 0; i < numOfTrial; i++) { // 3回ダイスを振る var val = 0; for (var j = 0; j < rollNum; j++) { val = RollDice() + RollDice() + RollDice(); } if (dic.ContainsKey(val)) { dic[val]++; } else { dic.Add(val, 1); } } // もし値が入ってない場合には0を詰める for (var j = 1; j < rollNum * 6 + 1; j++) { if (!dic.ContainsKey(j)) { dic.Add(j, 0); } } return dic; } } } |
結果は以下となりました。
| 試行回数 | 確率 | 相対誤差 ((測定値-理論値) / 理論値 × 100) |
|---|---|---|
| 計算 | 0.11574074074074074 | 0 % |
| 101 | 0.09900990099009901 | 14.455445544 % |
| 10001 | 0.1192880711928807 | 3.06489351 % |
| 1000001 | 0.11562688437311562 | 0.098371901 % |
| 100000001 | 0.11575254884247452 | 0.010202199 % |
試行回数を増やすごとに誤差が減っていくことがわかります。
3 回サイコロを振った時の出目は 3~18 となるので、各出目についての確率を分布にしてみました。
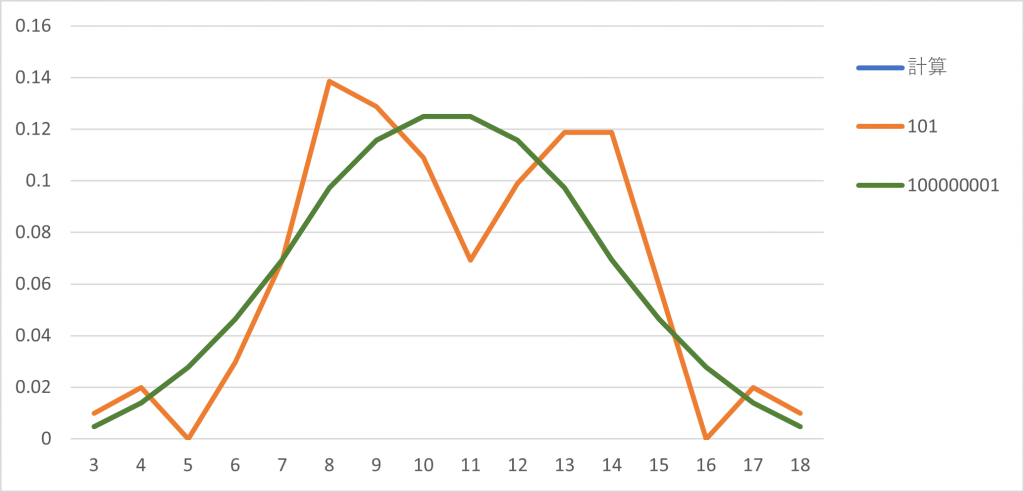
計算の青色の折れ線は100000001回の緑色の折れ線とほぼ一致しているので隠れて見えません。
このことから試行回数が十分多い場合は理論上の計算値とほぼ同等の結果を得ることができたといえます。
例2: 円周率の計算
前述の説明ではすごく単純なモデルを考えてみました。
モンテカルロ法の例としてよく用いられる円周率の計算をしてみましょう。
円周率 ![]() と言うのはよく知られた事実なのですが、この円周率をモンテカルロ法で計算してみたいと思います。
と言うのはよく知られた事実なのですが、この円周率をモンテカルロ法で計算してみたいと思います。
円周率の定義とは以下のようになります(小学生で習う内容ですが念のため)
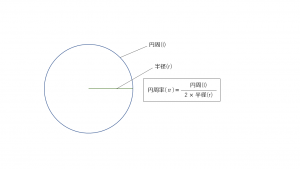
プログラムで求める時に上記のパラメータをどうにかして出すのは少し難しそうです。
半径をなにか値を定めた時に直径がわかれば円周率が出せるのですが、方法が思いつかないです。
そこで少し考え方を変えて、円の面積を考えてみましょう。
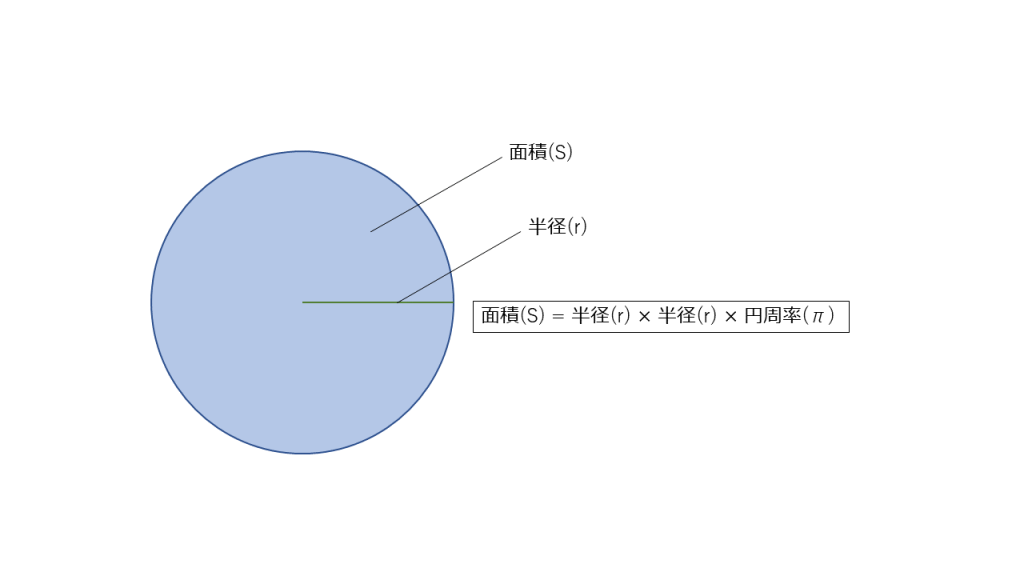
こちらにも円周率がでてきます。
ここからならプログラムで円周率を求める糸口が見えてきそうです。
ある正方形の領域に点をランダムに打ちます。
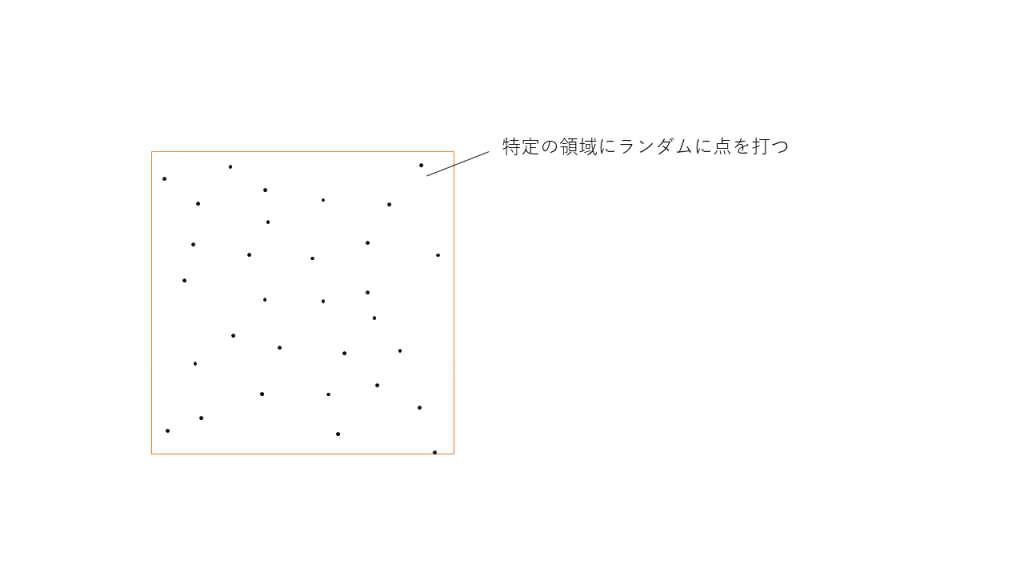
その領域に接するように円を考えた時、円内にある点と正方形全体にある点の関係は以下のようになります。
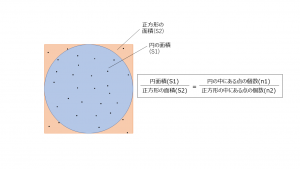
円の半径を ![]() とすると、正方形の 1 辺は
とすると、正方形の 1 辺は ![]() となります。
となります。
円の中にある点の個数を ![]() 、正方形の中にある点の個数を
、正方形の中にある点の個数を ![]() とすると、円周率の計算式は計算式は省略しますが以下となります
とすると、円周率の計算式は計算式は省略しますが以下となります
![]()
すごくシンプルですね。
![]() と
と ![]() はプログラムで出力することはできそうです。
はプログラムで出力することはできそうです。
上記を計算するようなプログラムは以下です
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
using System; namespace ConsoleApp3 { class Program { static void Main(string[] args) { var num = 101; Console.WriteLine("n = " + num + ", Pi : " + Pi(num)); num = 10001; Console.WriteLine("n = " + num + ", Pi : " + Pi(num)); num = 1000001; Console.WriteLine("n = " + num + ", Pi : " + Pi(num)); num = 100000001; Console.WriteLine("n = " + num + ", Pi : " + Pi(num)); } private static readonly Random random = new(); private static double RandomDot() { return random.NextDouble() * 2 - 1d; } public static double Pi(int dotNum) { var circleDot = 0; for (var i = 0; i < dotNum; i++) { var x = RandomDot(); var y = RandomDot(); if (Math.Pow(x, 2) + Math.Pow(y, 2) < 1) { circleDot++; } } return circleDot * 4 / (double)dotNum; } } } |
結果は以下となりました。
| 試行回数 | 確率 | 相対誤差 ((測定値-理論値) / 理論値 × 100) |
|---|---|---|
| 101 | 3.207920792079208 | 2.111290221334839 % |
| 10001 | 3.122887711228877 | 0.5953968073977544 % |
| 1000001 | 3.1432328567671433 | 0.05220928867006153 % |
| 100000001 | 3.141663688583363 | 0.0022611140718324692 % |
試行回数を増やすとかなり精度の高い円周率を取得することができました。
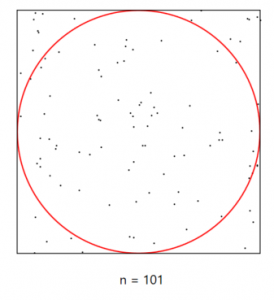
101回と10001回のランダムでドットを打った図は以下となります

おわりに
今回はモンテカルロ法というシミュレーション方法を紹介しました。
今後はこのシミュレーションを用いて、一見どのように計算したら良いかわからない確率を計算して考察していけたら良いなと思います。

